新时代主动配电网中“源-荷-储”协同优化调度的研究与应用，主动配电网中“源-荷-储”协同优化调度的研究及应用实现

主动配电网中“源-荷-储”协同优化调度研究

ID:75360712914961650

Herr方

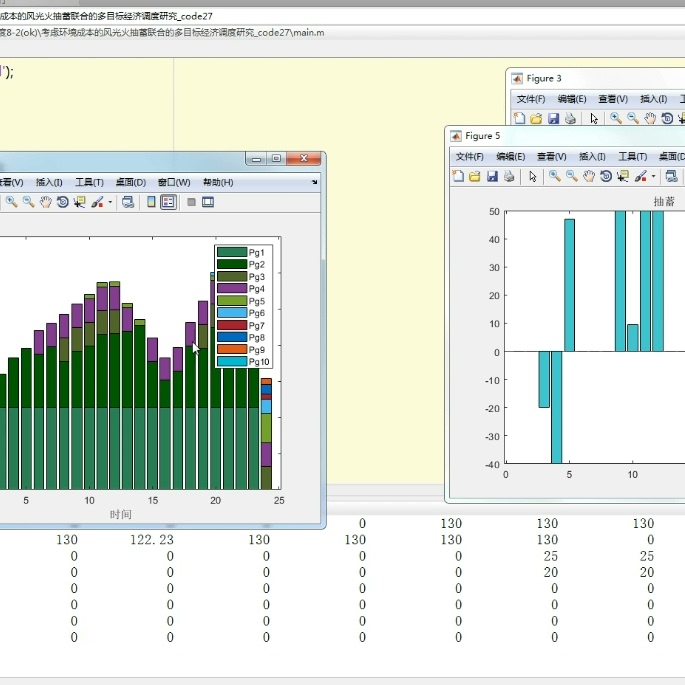
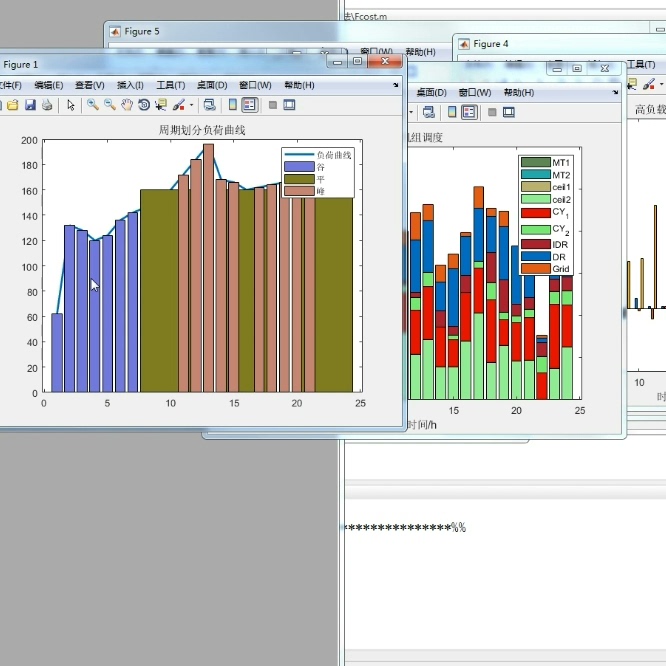
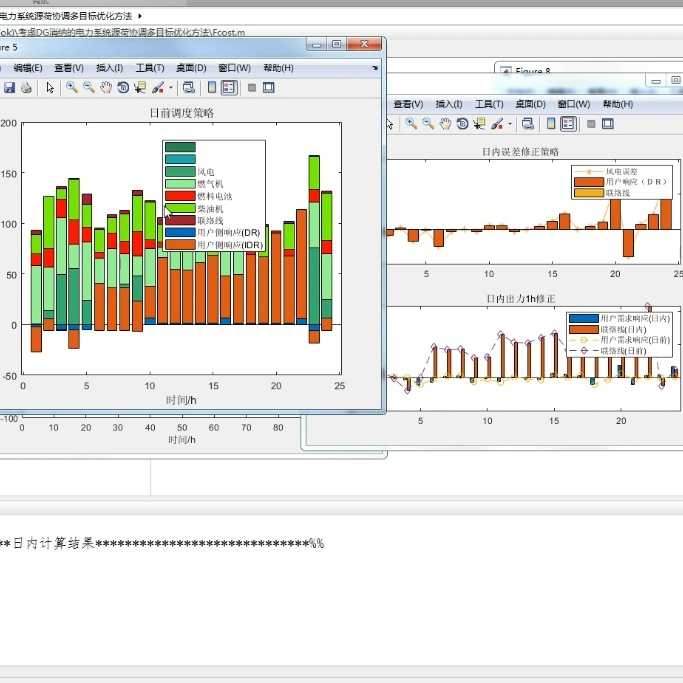
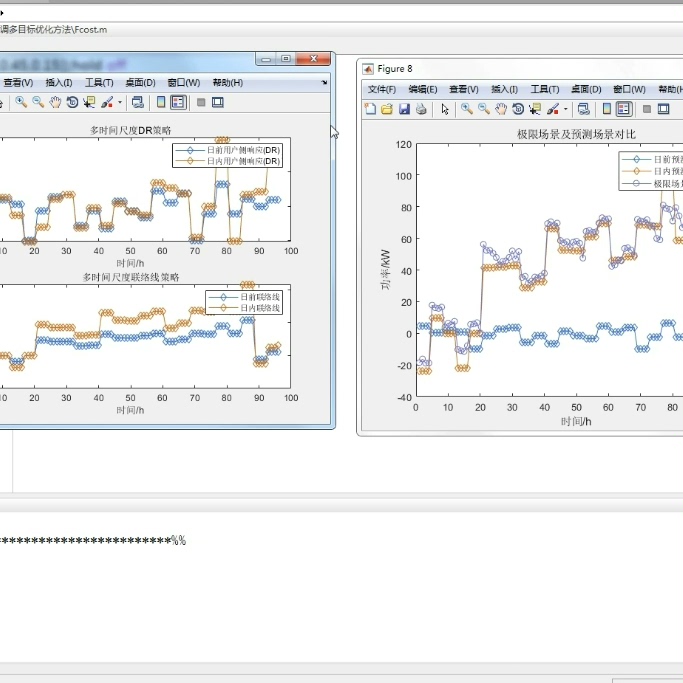
主动配电网是指利用先进的通信、计算和控制技术实现对电网中各个节点的实时监测、通信和控制，从而实现电力系统的智能化运行。在主动配电网中，源、荷、储三者之间的协同优化调度是实现电力系统优化运行的关键。

在传统的配电网中，电力系统的供需平衡主要依靠中央调度进行控制。而在主动配电网中，由于具有分布式能源、电动汽车、储能系统等新兴电力设备的接入，电力系统变得更加分散和复杂。因此，如何协调这些不同节点之间的能源供需关系，使得系统运行效率最大化，成为了主动配电网中的重要问题。

为了实现源、荷、储协同优化调度，首先需要建立一个能够实时监测和控制各个节点的监测系统。通过这个系统，可以实时获取各个节点的电力信息，包括电流、电压、功率等数据。同时，还需要建立一个通信系统，将这些数据传输给中央控制系统。

在确定了各个节点的电力信息后，接下来就是要进行优化调度。优化调度的目标是通过合理调度各个节点的能源供给和能量消耗，使得系统的总体运行效率最大化。一种常用的优化调度方法是基于数学模型的优化算法。通过建立数学模型，将能源供给和能量消耗与系统的运行效率联系起来，然后使用优化算法求解最优解。常用的优化算法有线性规划、整数规划、遗传算法等。

同时，优化调度还需要考虑到电力系统的安全性和稳定性。例如，在供电不足或者供电过载时，需要进行相应的调整。为了实现这一点，可以采用柔性配电技术，即通过灵活调整节点的运行模式和电力配置，来适应不同的运行需求。

除了源、荷、储之间的协同优化调度，主动配电网还可以实现对电网的实时监测和检测。通过建立监测系统和传感器网络，可以实现对电力设备的状态监测和故障检测。一旦发现设备故障，可以及时采取相应的措施进行修复，从而提高电力系统的可靠性和稳定性。

总之，主动配电网中的源、荷、储协同优化调度是实现电力系统优化运行的重要环节。通过建立监测系统、通信系统和优化调度算法，可以实现对电网节点的实时监测和控制，并通过合理调度各个节点的能源供给和能量消耗，实现系统的优化运行。同时，还可以通过柔性配电技术和故障监测系统来提高电力系统的安全性和稳定性。

【相关代码,程序地址】：http://fansik.cn/712914961650.html