基于相关滤波器的追踪（Correlation Filter-based Tracking）原理

基于相关滤波器的追踪（Correlation Filter-based Tracking）原理

基于相关滤波器的追踪算法，典型的算法有KCF，DSST，STC，SAMF等。这些算法的大致框架都是差不多的。

介绍

在视频的第一帧给定目标的初始位置，追踪的目标就是预测目标之后的位置。追踪受到很多因素影响，比如光照变化（illumination variations），遮挡，形变，旋转等。在过去对于追踪的研究之中，主要分为2中方法：生成型模型（generative model）和判别式模型（discriminative models）。前者的主要思想就是通过寻找最佳匹配的窗口，而后者的主要思想就是学习从背景中区分目标。

在判别式模型中，基于相关滤波器的追踪算法（Correlation Filter-based Tracking）表现比较好。一般的，相关滤波器的原理就是在场景中，对每个感兴趣的目标产生高响应（相关峰（correlation peak）），对于背景则产生低的响应。

Correlationfilter-based tracking（CFTs）主要可以通过以下几个方面提高：

1）引入更好的训练方案（introducing better training schemes）

2）提取更强大的特征（extracting powerful features）

3）减轻尺度变化的影响（relieving scaling issue）

4）结合基于部分的追踪策略（applying part-based tracking strategy），即相对于对目标整体识别，可以将目标分成好几个部分，对各个部分进行识别

5）结合long-term的追踪（cooperating with long-term tracking）。

CFT整体框架介绍

          对于输入的第一帧，将给定的要追踪的区域提取出特征，然后进行训练，得到相关滤波器。

          对于之后的每一帧，先裁剪下之前预测的区域（由于是对前一帧区域做相关，所以对于物体快速移动处理的不好），然后进行特征提取，这些特征经过cos窗函数之后，做FFT变换，然后与相关滤波器相乘，将结果做IFFT之后，最大响应点所在的区域即为要追踪目标的新位置，然后再用新位置区域训练更新得到新的相关滤波器，用于之后的预测。

         详细的框架如下图：

用数学的方式描述工作流程如下：

         x：检测器的输入。要么是rawimage patch，要么是提取的特征；

         h：相关滤波器。

         根据卷积理论，时域上的卷积相当于频域上的乘积，可以得到如下式子：

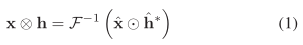
符号‘^’表示傅里叶变换，⊙表示element-wise相乘，*表示复共轭，F^-1表示反傅里叶变换。（1）的结果就是x与h的相关输出，也就是之前提到的confidence map，根据最大的响应位置，可以得到目标新预测的位置。

         对于训练滤波器，我们首先定义一个期望的相关输出y（可以是任意形状，比如MOSSE算法就是将y定义为2D峰值在中心的高斯分布的函数，UMACE算法就是目标中心点为1，其余位置为0的Kronecker delta函数）。使用目标的新实例x’，相关滤波器h应该满足：

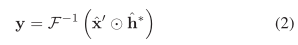
因此：

其中， 表示y的DFT，除法的计算也是element-wise的。

 

对于一幅n x n大小的图片进行循环卷积的计算复杂度是O(n⁴)，而使用FFT之后，计算复杂度变为O(n²logn)，因此使用FFT的加速作用很明显。