SOLIDWORKS「点击」和「双击」修改尺寸如何切换

在SOLIDWORKS修改草图尺寸一般用两种的方法，【双击】尺寸修改数值 和 【单击】数字修改数值，两种方法各有优缺点：

【双击】修改时：会弹出一个修改窗口，比较直观，还带有一些其他功能；但如果仅仅是修改尺寸的话，这一步会影响操作速度，显得有点鸡肋。

【单击】修改时：速度会有所提高；但有时候我只是想拖动一下标注的位置，并不想修改尺寸，可能会出现误操作的情况。

演示过程

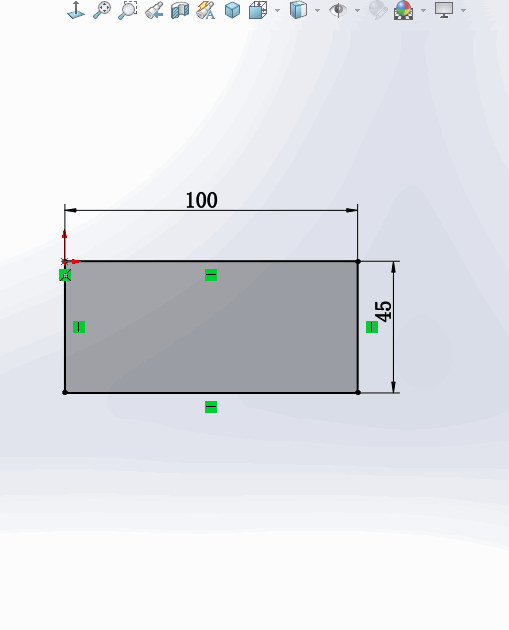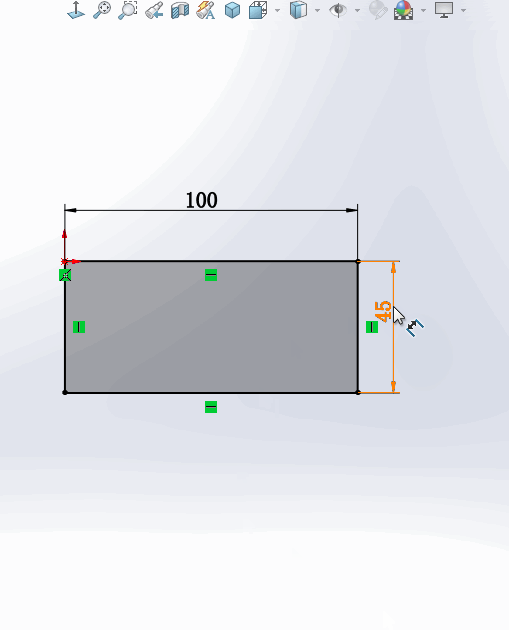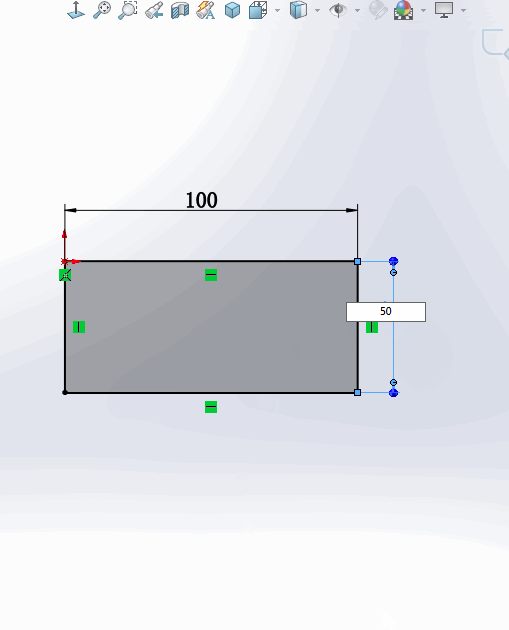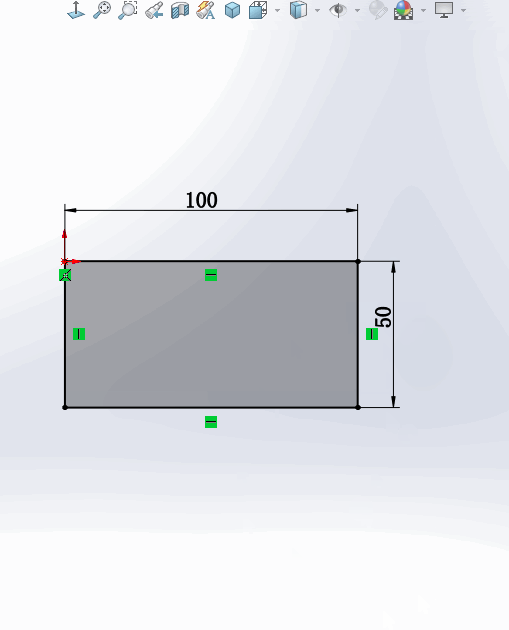
1.在绘制草图的过程中，如果要修改一个尺寸，一般情况下要【双击】这个标注，这时会弹出【修改】窗口，输入数字才能修改该尺寸。

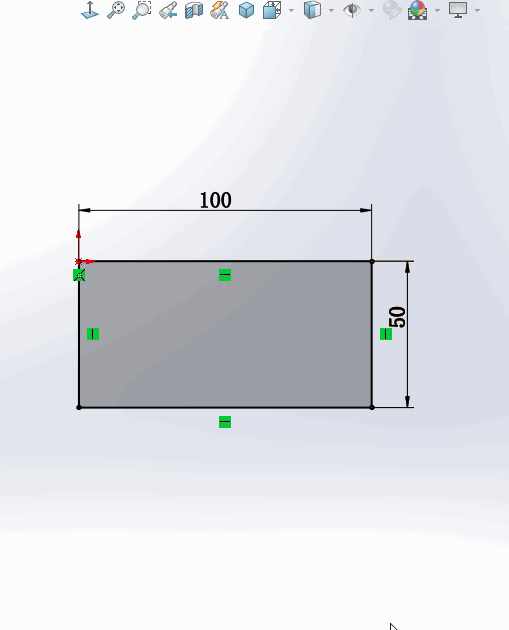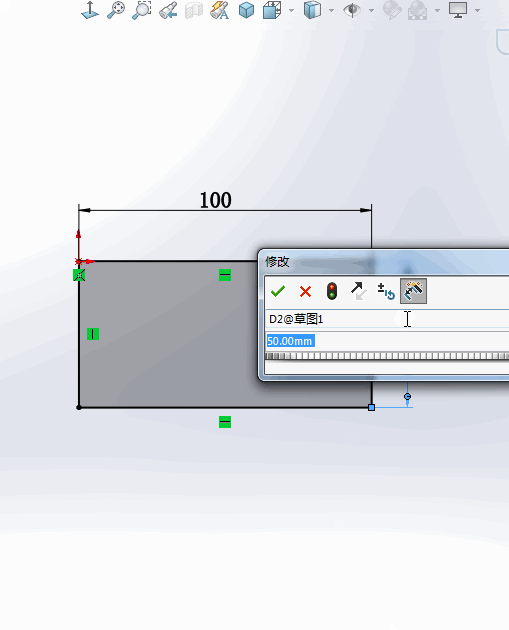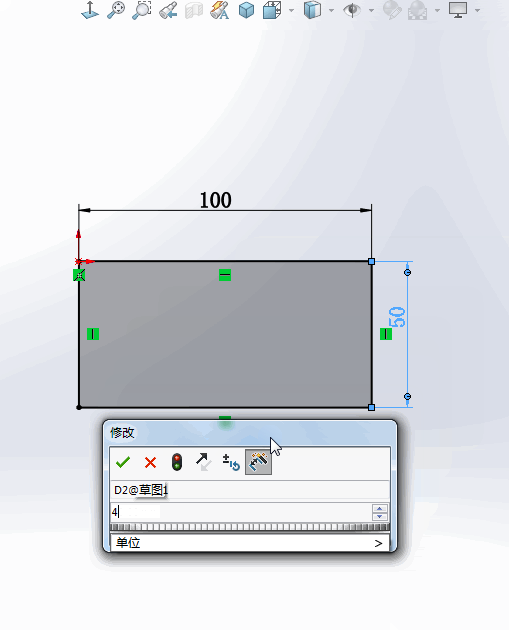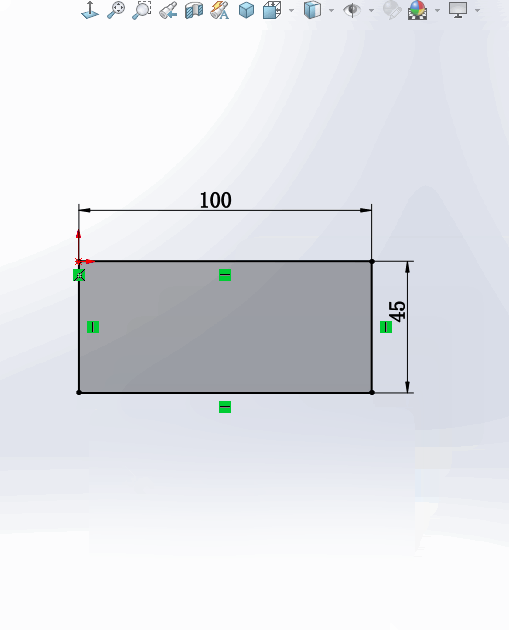
2.还有一种情况是：只需要【点中】这个数字，就可以直接修改尺寸。没有了弹出窗口这一步，速度大大提高。

3.那该怎么切换呢？非常简单：打开【Instant2D】就是【单击】；关闭【Instant2D】就是【双击】 。

 

4.用GIF动图演示一下：

 

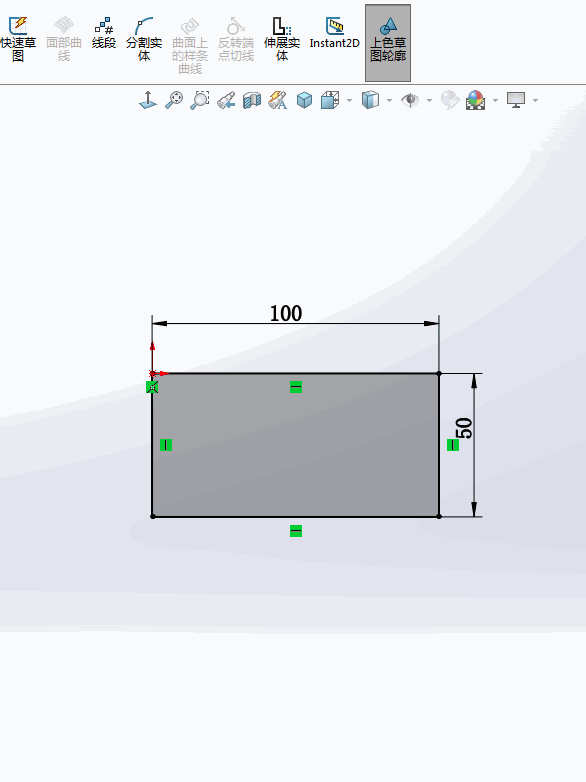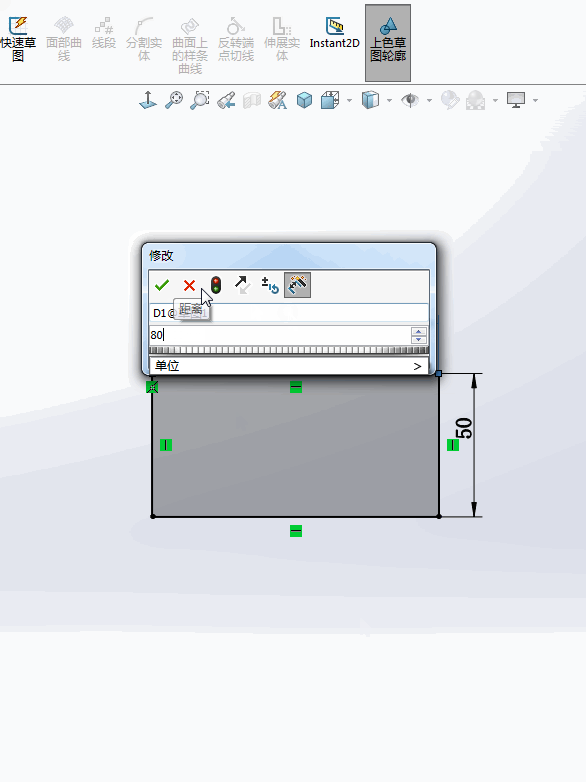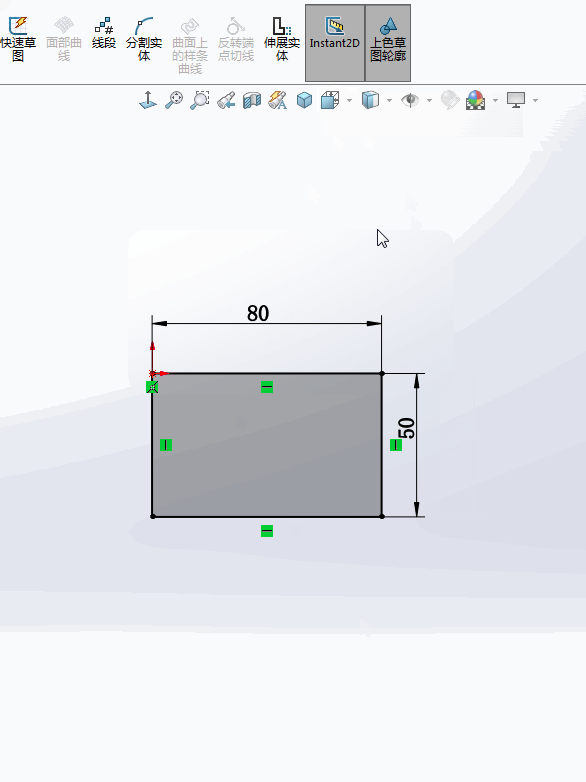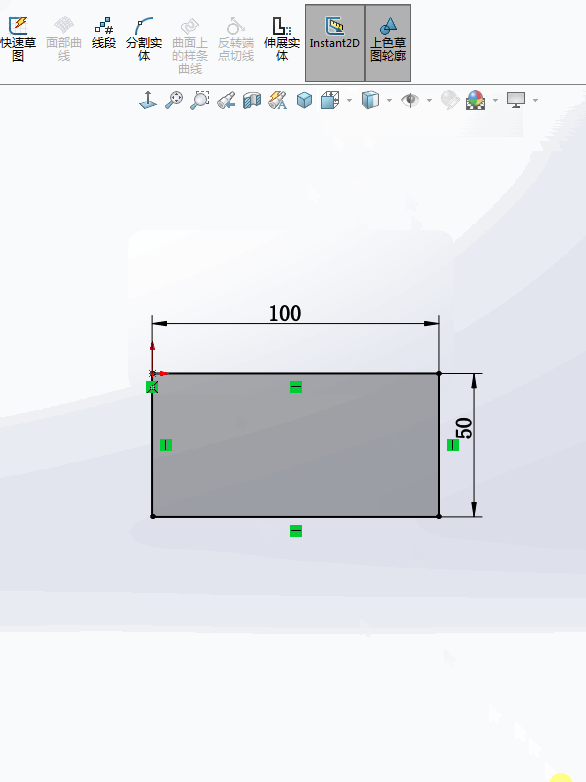
更多SOLIDWORKS资讯，请关注数领科技。