[无监督学习] 16.详细图解LLE

LLE
无监督学习中的一项重要任务是将结构复杂的数据转化为更简单的形式。
LLE（Locally Linear Embedding，局部线性嵌入）可以将以弯曲或扭曲的状态埋藏在高维空间中的结构简单地表示在低维空间中。

概述
LLE 是一种被称为流形学习（manifold learning）的算法，它的目标是对具有非线性结构的数据进行降维。下面来看一下具体的例子。
图 3-25a 是经常作为非线性数据的例子的瑞士卷（Swiss rolls）数据集的图形。瑞士卷数据集就像一个二维结构（长方形）被卷曲后埋藏在三维空间中的数据集。我们将 LLE 和 PCA 应用于该数据集，降维至二维后的结果分别如图 3-25b 和图 3-25c 所示。LLE 可以把埋藏在三维空间中的二维结构取出，将其以二维数据表示。PCA 则采取像是将原始数据压扁的方式进行降维。由于 PCA 适用于变量之间存在相关性的数据，所以在对瑞士卷数据集这种非线性数据降维时，更适合采用 LLE 这样的方法。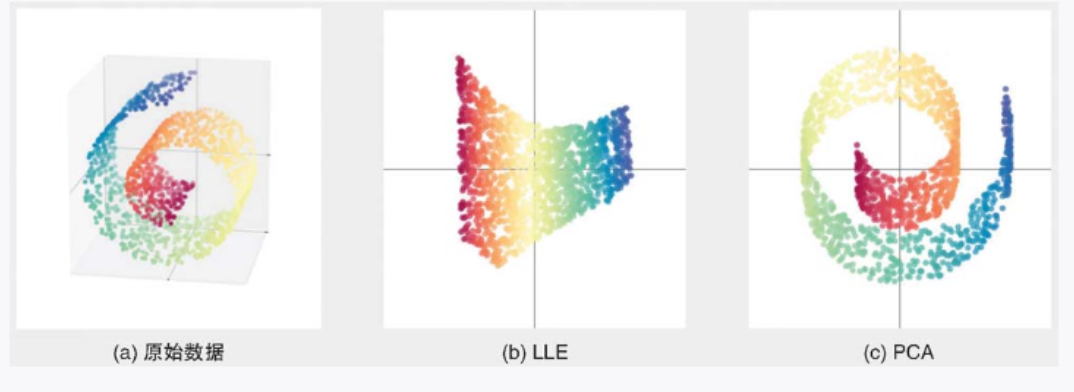

▲图 3-25　瑞士卷数据 (a)、应用 LLE 的结果（近邻点的数量：12）(b) 和应用 PCA 的结果 (c)

算法说明
LLE 算法要求数据点由其近邻点的线性组合来表示。我们看一个例子：对于数据点x1，以最接近 x1 的两个点 x2 和 x3 的线性组合来表示它。图 3-26 中的左图是当 时的情况，如果 x2 和 x3 的权重分别为那么 x1 可以表示为 。如果在不扭转三维空间的 3 个点之间的关系的前提下把它们移动到二维空间，我们就可以继续使用这些权重来以近邻点表示 x1。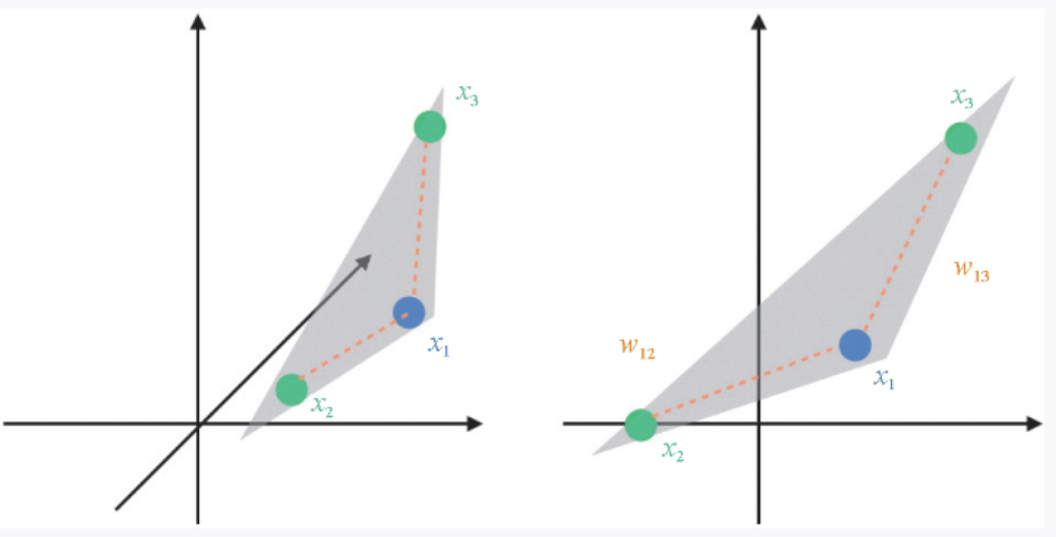

▲图 3-26　近邻点的示意图

实际的数据虽然在三维空间上呈现瑞士卷那样的卷曲结构，但 LLE 将其视为局部的点与点的关系，即近邻点之间是不弯曲的空间，所以仍使用近邻点来表示数据点。

下面对 LLE 算法进行说明。假设在 D 维空间内存在一个d 维空间的结构（d < D），使用图 3-27 所示的步骤进行降维。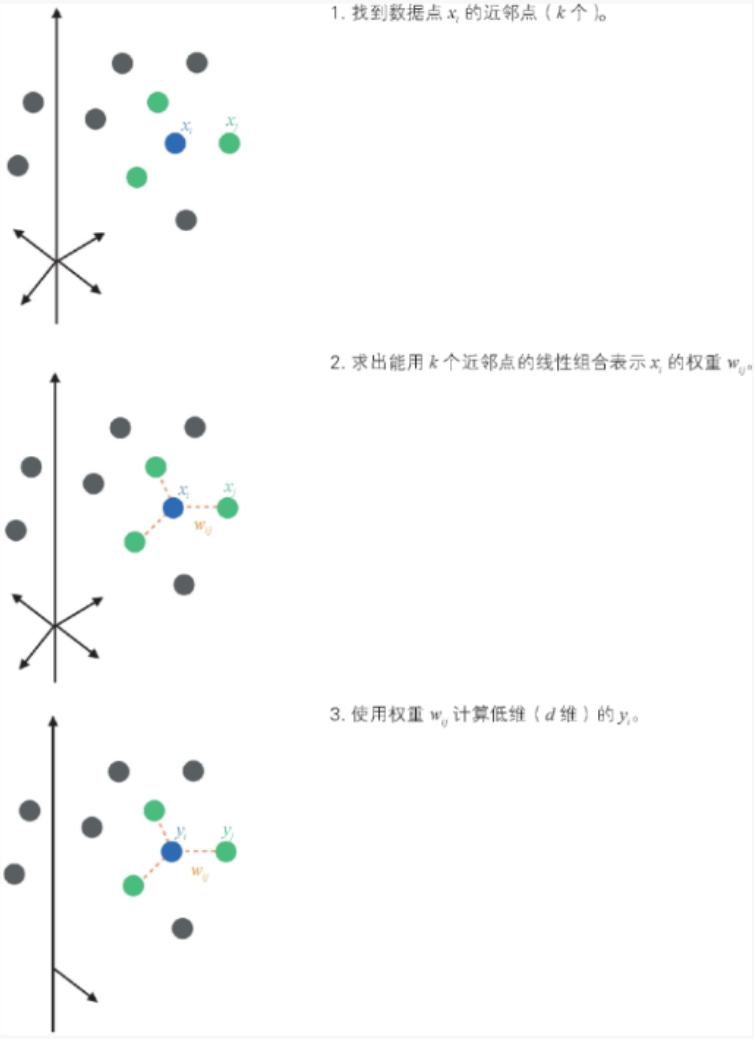

▲图 3-27　LLE 算法示意图

考虑数据点 xi 的近邻点是 LLE 的特点。
在确定近邻点数量后，首先，为了求出权重 wij，我们将 xi 和“xi 的近邻点的线性组合”的误差表示为 。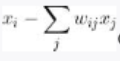
随着 wij 值的变化，这个误差会增大或减小。
通过计算所有 xi 和线性组合的差的平方和，我们将权重 wij 与误差之间的关系表示为以下误差函数：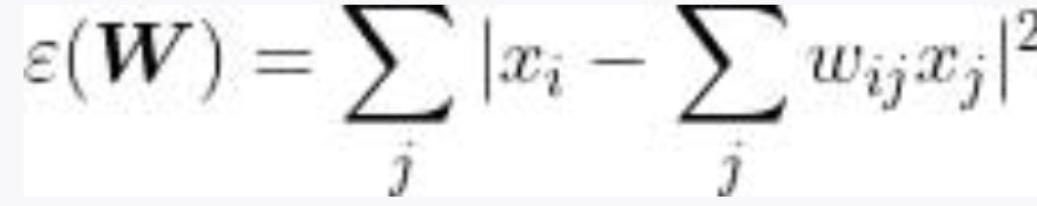

除了 wij 近邻点之外，表达式的值都是 0。另外还有一个约束条件：对于某个 i，有 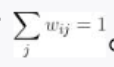（如上述说到的）。我们可以认为权重 wij 表示数据点 xi 及其近邻点之间的关系，而且这种关系在低维空间中也得以保持。在计算完权重后，我们计算在低维空间中表示数据点的yi：

前面求出了使误差最小的权重 wij，现在要做的是利用刚刚求出的 wij，求使误差最小的 y。

示例代码
下面是对瑞士卷数据集应用 LLE 的代码，其中设置的近邻点的数量为 12。

import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding

# 生成瑞士卷数据
data, color = make_swiss_roll(n_samples=1500)

# 定义近邻点的数量和降维后的维度
n_neighbors = 12
n_components = 2

# 创建和拟合LLE模型
model = LocallyLinearEmbedding(n_neighbors=n_neighbors,
                               n_components=n_components)
transformed_data = model.fit_transform(data)

print(data)
print("*******************3d to 2d*******************")
print(transformed_data)

# 可视化原始瑞士卷数据
fig = plt.figure(figsize=(12, 6))

ax = fig.add_subplot(121, projection='3d')
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c=color, cmap='hot')
ax.set_title('Original Swiss Roll')

# 可视化降维后的数据
ax = fig.add_subplot(122)
ax.scatter(transformed_data[:, 0], transformed_data[:, 1], c=color, cmap='hot')
ax.set_title('LLE Reduced Swiss Roll')

plt.show()

结果：

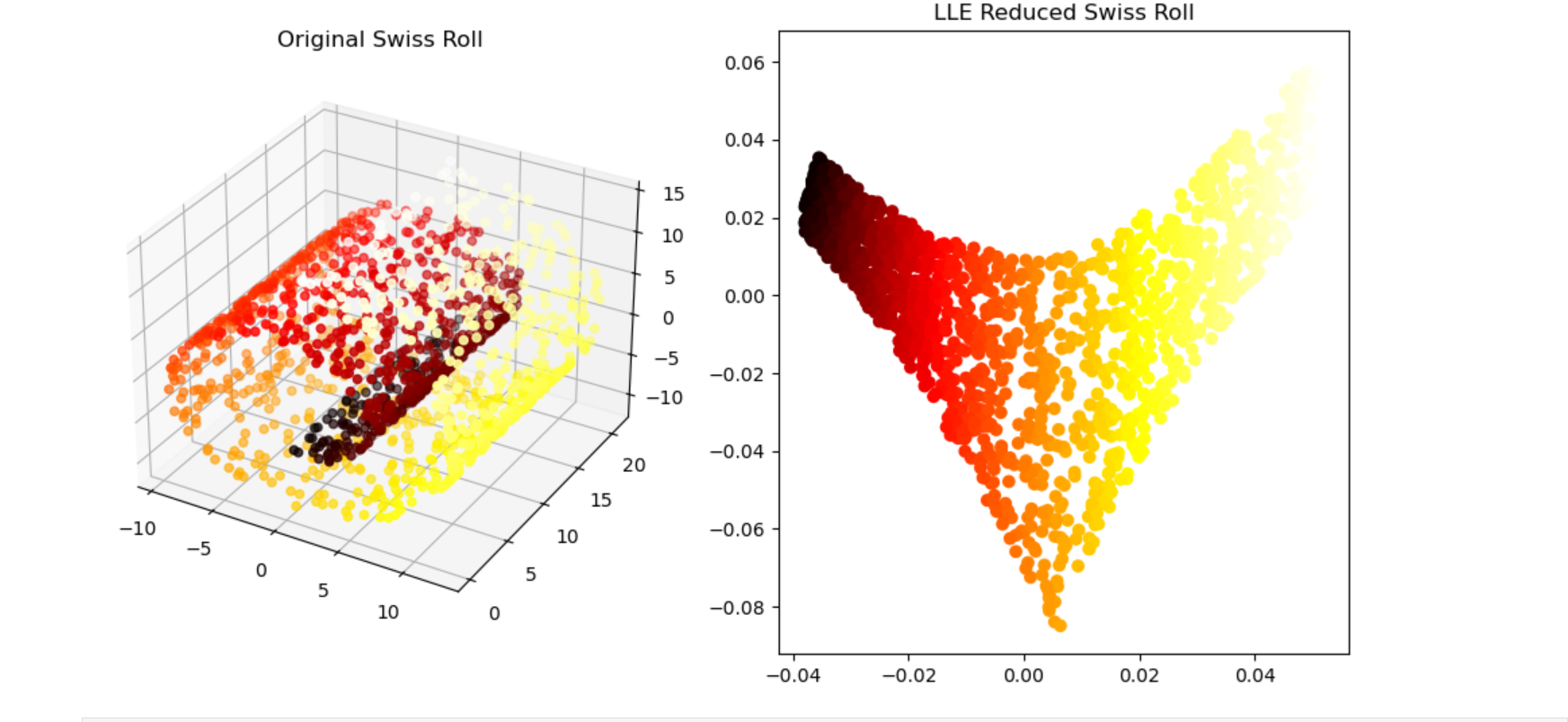
详细说明
关于流形学习
LLE 和下一节将介绍的 等针对非线性数据的降维算法被统称为流形学习。流形指的是可以将局部看作没有弯曲的空间。类似地，地球虽然是球体，但是我们可以对地球的局部绘制平面地图。只要理解“所谓的流形就是从局部来看是低维空间的结构被埋藏在高维空间里”就足够了。通过以 LLE 为首的各种各样的流形学习算法，可以找到（在弯曲或扭曲的状态下）埋藏在高维空间中的低维的数据结构。

近邻点的数量
LLE 的近邻点数量需要被定义为超参数。
在对图 3-25a 所示的瑞士卷数据应用 LLE 时，将近邻点的数量分别设置为 5 和 50，结果如图 3-28 所示。当近邻点的数量被设置为 5（图 3-28a）时，LLE 没能取出连贯的结构，所以降维后的点的分布显得不是很宽，看上去聚集在一个狭窄的区域，这并不能反映太多的信息。当近邻点的数量被设置为 50（图 3-28b）时，不同颜色的点离得很近。这是由于近邻点的数量太多，无法把握局部的结构。因为近邻点的数量对 LLE 结果影响较大，所以必须慎重设置。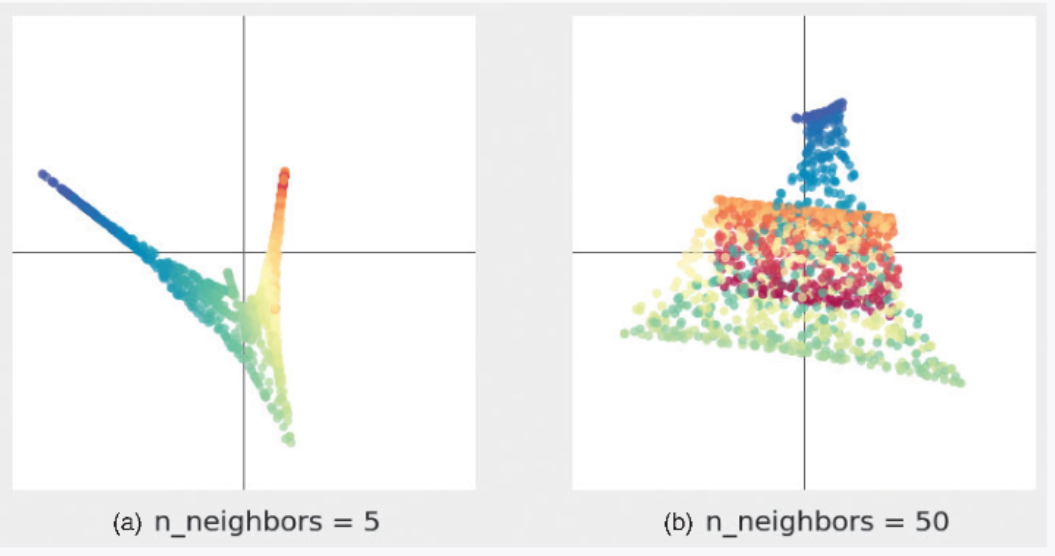

▲图 3-28　不同的近邻点数量导致 LLE 结果不同（(a) 的近邻点数量为 5，(b) 的近邻点数量为 50）

———————————————————————————————————————————

文章来源:书籍《图解机器学习算法》

作者：秋庭伸也 杉山阿圣 寺田学

出版社：人民邮电出版社

ISBN：9787115563569

本篇文章仅用于学习和研究目的，不会用于任何商业用途。引用书籍《图解机器学习算法》的内容旨在分享知识和启发思考，尊重原著作者秋庭伸也 杉山阿圣 寺田学的知识产权。如有侵权或者版权纠纷，请及时联系作者。
——————————————————————————————————————————