【对抗攻击论文笔记】Improving Transferability of Adversarial Examples with Input Diversity

最新推荐文章于 2024-04-24 09:35:15 发布

nanyidev

最新推荐文章于 2024-04-24 09:35:15 发布

阅读量1.3k

点赞数 2

分类专栏： # 论文笔记文章标签：深度学习人工智能计算机视觉

本文链接：https://blog.csdn.net/ji_meng/article/details/125032399

版权

论文笔记专栏收录该内容

5 篇文章 3 订阅

订阅专栏

文章目录

论文概述
- idea
- method
详细内容

论文概述

来自CVPR2019，论文链接：pdf——通过输入多样性提高对抗性示例的可迁移性

idea

最核心的idea就是对输入进行变换来增加迁移性，可以是rotating，flipping等，作者在文中说是受到数据增强（data augmentation）的启发。同时，也有文章表明图像变换可以防御对抗样本，攻击者可以将其用作benign 样本以产生更多可转移的对抗样本（正文中也有对motivation的阐述）

method

主要就是对输入的图像进行变换，变换的公式可以见下文内容

详细内容

摘要

大多数现有的对抗性攻击仅在具有挑战性的黑盒设置下取得相对较低的成功率，其中攻击者不了解模型结构和参数。为此，我们建议通过创建diverse input patterns（不同的输入模式）来提高对抗样本的可迁移性。我们的方法不是仅使用原始图像生成对抗样本，而是在每次迭代时对输入图像应用随机变换。 ImageNet 上的大量实验表明，所提出的攻击方法可以生成对抗样本，这些样本可以比现有baseline更好地迁移到不同的网络。

1.介绍

（不同于以往文章介绍中对攻击的分类（白盒和黑盒），本文聚焦于single-step attacks and iterative attacks分类，一般来说迭代攻击对于白盒攻击成功率更高，但迁移性不够好，所以单步攻击对黑盒性能更好）

这种权衡是由于迭代攻击倾向于过度拟合特定的网络参数（即白盒成功率高），因此生成的对抗样本很少转移到其他网络（即黑盒成功率低），而单步攻击通常不适合网络参数（即，具有低的白盒成功率），因此产生的对抗样本具有稍好的可迁移性。观察这一现象，一个有趣的问题是我们是否可以在白盒和黑盒设置下生成具有高成功率的对抗样本。

我们将提出的 input diversity strategy（输入多样性策略）与迭代攻击相结合，例如 I-FGSM [17] 和 MI-FGSM [9]。在每次迭代中，与直接最大化损失函数的传统方法不同。我们以概率 p 对输入图像应用随机和可微的变换（例如，随机调整大小、随机填充）并最大化损失函数。请注意，这些随机操作以前用于防御对抗样本[38]，而在这里我们将它们合并到攻击过程中以创建困难和多样化的输入模式。

2.相关工作

（主要就是介绍了攻击和防御）

3.方法

（首先介绍了对抗攻击的一些定义）

3.1 FGSM家族

（介绍了FGSM，I-FGSM，MI-FGSM，就贴个公式吧）
FGSM：
在这里插入图片描述
I-FGSM：

MI-FGSM：

3.2 motivation

（主要讲了本文的动机，首先说了传统的单步攻击如FGSM往往欠拟合这样攻击准确率就不高，而多步攻击如I-FSGM往往过拟合，这样迁移性就不好。
然后就说数据增强是防止过拟合的有效方法，如果对输入进行了图像变换，那么这些变换后的对抗样本就是 good samples for better optimization）

3.3 Diverse Input Patterns

（终于要讲怎么做了）
DI2-FGSM
首先，我们提出了多样化输入迭代快速梯度符号方法（DI2-FGSM），该方法在 I-FGSM [17] 的每次迭代中以概率 p 将图像变换 T (·) 应用于输入，以减轻过拟合。

在本文中，我们考虑随机调整大小和随机填充作为图像变换 T (·) 的实例化。变换概率 p 控制白盒模型的成功率和黑盒模型的成功率之间的权衡，如果 p = 0，则 DI2-FGSM 退化为 I-FGSM 并导致过拟合。如果 p = 1，即仅使用转换后的输入进行攻击，则生成的对抗样本在黑盒模型上的成功率往往更高，但在白盒模型上的成功率较低。

DI2-FGSM公式：
在这里插入图片描述
其中随机变换函数T的表达式是：
$T(X_n^{adv};p)=\begin{cases} T(X_n^{adv}) & p\\ X_n^{adv} & 1-p \\ \end{cases}$

M-DI2-FGSM
直观地说，动量和不同的输入是缓解过拟合现象的两种完全不同的方法。我们可以将它们自然地结合起来形成更强的攻击，即动量多样化输入迭代快速梯度符号法（M-DI2-FGSM）。 M-DI2-FGSM 的整体更新过程与 MI-FGSM 类似，只是替换了 Eq. (4) ，公式如下：
在这里插入图片描述

3.4不同攻击之间的关系
在这里插入图片描述

3.5 Attacking an Ensemble of Networks
在MI-FGSM中（论文pdf）已经提到过集成的攻击方法，这里follow过来。具体来说，为了攻击 K 个模型的集合，logits 通过以下方式融合：
$l(X;\theta_1,\cdots,\theta_k) = \sum_{k=1}^K w_k l_k(X;\theta_k)$
其中 $l_k(X; θ_k)$ 是参数为 $θ_k$ 的第 k 个模型的 logits 输出， $w_k$ 是权重且 $\sum_{k=1}^K w_k = 1$

4.实验结果

4.1 实验设置
（数据、模型，实验细节）

4.2 Attacking a Single Network

在这里插入图片描述
从表 1 中可以看出，M-DI2-FGSM 在所有黑盒模型上的性能都大大优于所有其他baseline攻击，并且在所有白盒模型上都保持了很高的成功率。

4.3 Attacking an Ensemble of Networks
在这里插入图片描述
在六个网络的集合上生成对抗样本，并分别使用 I-FGSM、DI2FGSM、MI-FGSM 和 M-DI2-FGSM 在集成网络（白盒）和hold-out网络（黑盒网络）上进行测试。 FGSM 在此被忽略，因为它在白盒模型上的成功率很低。所有集成模型都被赋予相同的权重，即 wk = 1/6

4.4. Ablation Studies
（对不同参数进行了消融实验）
Transformation probability p：我们首先研究了在白盒和黑盒设置下转换概率 p 对成功率的影响。我们设置步长 α = 1 和总迭代次数 $N=min(\epsilon+4,125\epsilon)$ ，变换概率 p 从 0 到 1 变化。

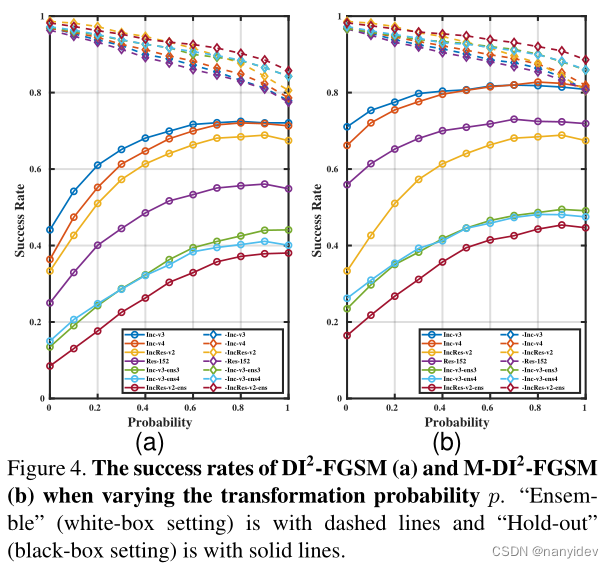
图a是DI2，图b是M-DI2，“Ensemble”（白盒设置）用虚线表示，“Hold-out”（黑盒设置）用实线表示。可以看到，白盒成功率随着 p 的增加而降低了。此外，对于所有攻击，如果 p 很小，即只使用少量的转换输入，黑盒成功率可以显着提高，而白盒成功率只会下降一点。这种现象揭示了将变换后的输入添加到攻击过程中的重要性

（后面还研究了Total iteration number N和Step size α对攻击的影响）