计算机中的小数 IEEE754

计算机中的小数 IEEE754

进制计数系统

在基数b的位置记数系统(其中b是一个正自然数，叫做基数)，b个基本符号(或者叫数字)对应于包括0的最小b个自然数。 要产生其他的数，符号在数中的位置要被用到。最后一位的符号用它本身的值，向左一位其值乘以b。一般来讲，若b是基底，我们在b进制系统中的数表示为

$$a_{0}b+a_1{b}^1+a_2{b}^2+...+a_k{b}^k$$

的形式，并按次序写下数字$a_0{a}_1{a}_2...a_k$。这些数字是0到b-1的自然数。

一般来讲，b进制系统中的数有如下形式：

$${\left(a_n{a}_{n-1}...a_0.c_1{c}_2{c}_3...\right)}_b=\sum _{k=0}^n{a}_k{b}^b+\sum _{k=1}^{\infty }{c}_k{b}^{-k}$$

上式成为一个b进制系统下的一个数字按位权的十进制下的展开式

数$b^k$和$b^{-k}$是相应数字在该位上的的比重，也称该位上的权重（位权）

进制互化

1. 十进制数化二进制整数部分除以二取余数，向上倒着写，小数部分乘以二取整数
   [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TB49uTxG-1598453896427)(https://www.runoob.com/wp-content/uploads/2018/11/210-1.png “十进制数化二进制”)]
2. 二进制数化十进制：按位权展开即可
   [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iXRT7ITB-1598453896429)(https://www.runoob.com/wp-content/uploads/2018/11/210-2.png “二进制数化十进制整数”)]
   [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SZVhGFom-1598453896431)(https://www.runoob.com/wp-content/uploads/2018/11/210-3.png “二进制数化十进制小数”)]

十进制与二进制互化的数学原理

假设一个十进制的数能够写成二进制的abc形式

那么这个十进制的数一定等于

$$a\times 2^2+b\times 2^1+c\times 2^0=\left(a\times 2^1+b\times 2^0\right)\times 2+c$$

那么这个数除以2，所得的余数是c,商是$a\times 2^1+b\times 2^0$，因此依次把余数倒过来写即可

再来看小数部分，.abc按权位展开得：

$$a\times 2^{-1}+b\times 2^{-2}+c\times 2^{-3}=\left(a+b\times 2^{-1}+c\times 2^{-2}\right)÷2$$

因为a要么是0，要么是1，而$b\times 2^{-1}+c\times 2^{-2}$肯定小于1大于等于0，因此小数部分乘以2，一定是0.xxxxx或者1.xxxx，整数部分是a，小数部分是$b\times 2^{-1}+c\times 2^{-2}$。当这这个数乘以2等于0时，把所有的整数数正过来写即可。

这既是方法也是原理

二进制小数的局限性

二进制无法表示全部的十进制小数，有一下例子：

二进制小数	十进制小数
0.1	0.5
0.01	0.25
0.001	0.125
0.0001	0.0625

因此我们可以推断，二进制小数能准确表达十进制小数的必要不充分条件为十进制小数最后一位是5

IEEE754 数据结构与科学计数法

一个二进制小数可以表示为（2进制下的科学计数法）：

$$V={\left(-1\right)}^s\times M\times 2^E$$

1. ${\left(-1\right)}^s$ 表示符号位，当 s=0，V 为正数；当 s=1，V 为负数
2. M 表示有效数字，大于等于 1，小于 2
3. $2^E$ 表示指数位

在IEEE 754标准中浮点数由三部分组成：符号位（sign bit），有偏指数（biased exponent）(阶码)，小数（fraction）（尾码）。浮点数分为两种，单精度浮点数（single precision）和双精度浮点数（double precision），它们两个所占的位数不同。

• 单精度浮点数（共32位）：
  1. 1个符号位
  2. 8个指数位
  3. 23个小数位
• 双精度浮点数（共64位）：
  1. 1个符号位
  2. 11个指数位
  3. 52个小数位

接下来笔者以单精度浮点数0.15625讲解浮点数的存储过程：
0.15625转化为二进制就是0.00101，然后将该数写成科学计数法（scientific notation），根据IEEE 754的规定，小数点的左边只能有一个1，所以最终的科学计数法形式是：

$$0.15625=0.00101_2=1.01_2\ast 2^{-3}$$

然后就可以得到小数部分为.012，指数部分为-3

最终在内存中的存储结果就是如下：
0|01111100|0100000000000000000000 = 0.15625

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9UtDJUCj-1598453896432)(https://www.runoob.com/wp-content/uploads/2018/11/003vshepzy6SKZgBFNG64690.png “0.15625”)]

下面对IEEE 754中的数据结构作解释：

1. 符号位（sign）：0，因为该数是正数（1表示负数）
2. 有偏指数（biased exponent）：有偏指数=实际指数+偏移量,因此在该例中-3 + 偏移量（bias）,在单精度浮点数中偏移量是127，因此127+(-3)=124，所以偏移指数是124。在双精度浮点数中偏移量是1023，因此偏移指数是1020，偏移值公式(n为有偏指数的位数)：$2^{n-1}-1$，不用补码而是偏移可以方便计算
3. 小数(fraction)：.01000000000000000000000

然而，IEEE 7454并没有简单的使用了上述定义，而是进行了扩充(n为阶码的位数)：

浮点数形式	阶码	尾数	描述
零	0	0	阶码是0，尾数的小数部分是0，这个数是±0（正负取决于符号位）
次正规数	0	非0	阶码是0，尾数的小数部分是非0，有效数字的整数部分为固定数值0。非规格化形式用于表示非常接近0的数。（指数偏移值为$2^{n-1}-2$）
正规数	[1,$2^n-2$]	任意	阶码位不包含全0和全1，尾数的小数部分为任意数值。有效数字的整数部分为固定数值1，使用隐含的方式表示，因此尾数只存储有效数字的小数部分。（指数偏移值为$2^{n-1}-1$）
无穷	$2^n-1$	0	阶码是$2^n-1$（阶码位全是1），尾数的小数部分是0，这个数是±∞（正负取决于符号位）
NaN	$2^n-1$	非0	指数是$2^n-1$，尾数的小数部分是非0，这个数表示为不是一个数（NaN）

0与次正规数

一般是某个数字相当接近零时，才需要使用非规格化形式来表示

小数点的左边都是以一个1开始的，为了节约内存，它们规定：所有数在小数点左边默认有一个1

按照这个规定的话，那么能够表示的最小的正规数就是：

$$0|00000001|00000000000000000000000=1.00000000000000000000000_2\times 2^{-126}$$

如果指数全为0，只能表示数字0的话，那么表示小数位的23位就没有利用起来。于是IEEE754的设计值，规定了一种新的数 次正规数（Subnormal Number Or Denormalize Number)。规定如下：

如果指数位全为0的话，那么在科学计数法中小数点的左边就默认为一个0，而不是1 这样的数，就被称为次正规数

在次正规数中所有的偏移指数位都是0，于是规定次正规数在单精度浮点数中指数应该为-126（并非-127），在双精度浮点数中指数应该为-1022（并非-1023）

所以最小的正数就应该是：

$$0|00000000|00000000000000000000001=0.00000000000000000000001_2\times 2^{-126}$$

避免突然式下溢出

假如没有次正规数，最小数应该是：

$$0|00000000|00000000000000000000000=1.0\times 2^{-127}$$

他到0的距离为$2^{-127}$

比他次大的数为

$$0|00000000|00000000000000000000001=1.00000000000000000000001_2\times 2^{-127}$$

两个数直接的距离，即相减得

$$0.00000000000000000000001_2\times 2^{-127}<2^{-127}$$

说明当两个非常接近的数相减得到一个无比接近于0的数，但是这个数小于0与可表示最小正数之间的距离，即无法表示这么小的数，只能舍入到0，叫做突然式下溢出

引入次正规数之后，最小数应该是：

$$0|00000000|00000000000000000000001=0.00000000000000000000001_2\times 2^{-126}$$

他到0的距离为$0.00000000000000000000001_2\times 2^{-126}$

最小的正规数应该是

$$0|00000001|00000000000000000000000=1.0\times 2^{-126}$$

比他次大的数为

$$0|00000001|00000000000000000000001=1.00000000000000000000001_2\times 2^{-126}$$

两个数直接的距离，即相减得

$$0.00000000000000000000001_2\times 2^{-126}=0.00000000000000000000001_2\times 2^{-126}$$

这说明引入次正规数，即使很小的数也可以表示出来，这种设计也是Intel公司极力推荐的，叫做渐进式式下溢出

一些特殊的值的表示方法（单精度）

说明：为了方便描述，最大值与最小值指绝对值的大小

浮点数形式	正负号	有效数字	实际指数	表示数值
负无穷	1	1.0	128	-∞
规格化最大值	1	2-$2^{-23}$	127	-(2-$2^{-23})\times 2^{127}$ = -3.4e+38
规格化最小值	1	1.0	-126	-$2^{-126}$ = -1.18e-38（-1.17549435e-38）
非规格化最大值	1	1-$2^{-23}$	-126	-(1-$2^{-23})\times 2^{-126}$ = -1.18e-38（-1.17549421e-38）
非规格化最小值	1	$2^{-23}$	-126	-$2^{-23}\times 2^{-126}$ = -1.4e-45
负零	1	小数部分是0	-127	-0.0
正零	0	小数部分是0	-127	+0.0
非规格化最小值	0	$2^{-23}$	-126	$2^{-23}\times 2^{-126}$ = 1.4e-45
非规格化最大值	0	1-$2^{-23}$	-126	(1-$2^{-23})\times 2^{-126}$ = 1.18e-38（1.17549421e-38）
规格化最小值	0	1.0	-126	$2^{-126}$ = 1.18e-38（1.17549435e-38）
规格化最大值	0	2-$2^{-23}$	127	(2-$2^{-23})\times 2^{127}$ = 3.4e+38
正无穷	0	小数部分是0	128	+∞
NaN	0或1	小数部分非0	128	NaN

0、无穷与NaN

以下运算会产生特殊数值：

NaN可以表示一个运算出错，表示非数字，虽然一些运算是有实际数学意义的例如负数单位i=根号下-1

为什么$2^{23}$个数可以表示无穷，岂不是浪费了？

原因：

1. NaN分为QNAN，SNAN，需要尾码的最高位区分
2. 用于NaN-boxing技术，即用剩下尾码的可用位把这个非数值表示出来，例如可以嵌入一个字符串，或者表示其他错误信息或代码

非均匀分布

我们知道指数有8位，尾数有23位，所以说每一个指数都可以表示$2^{23}$个小数，但是相邻两个指数的空间在增大，即：
$2^{n+1}-2^n=2^n$，也就是说，每一个指数表示的每一段小数空间的大小在成指数级增大，但是该空间内能表示的小数的个数却不变，因此该种方式表示的小数也是非均匀分布在数轴上的

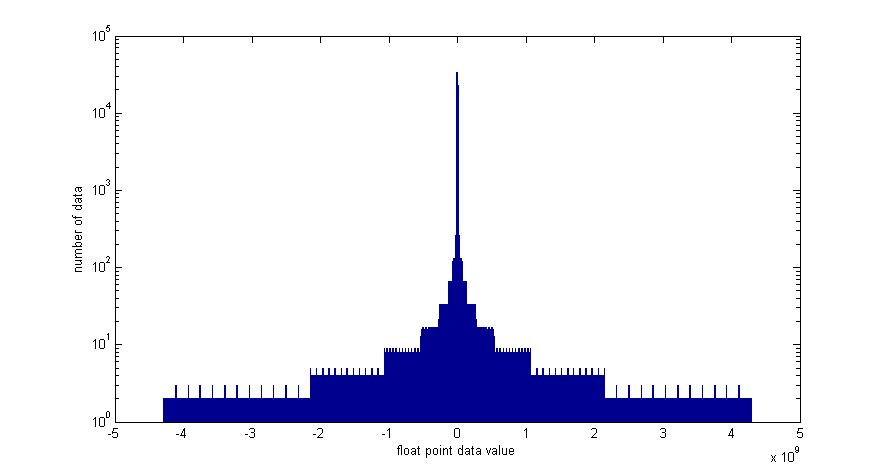
我们可以计算一下每一个指数表示的每一段小数空间中小数的间隔大小：

$$\frac{2^n}{2^{23}}=2^{n-32}$$

因此间隔大小成指数函数图像分布，距离先小后无比巨大，即分布先趋于紧密，后趋于稀疏

舍入模式

在存储单元的物理限制下，无限精度的浮点数需要根据需求进行舍入操作，一般可分为四类：

1. 最近舍入，即向距离最近的浮点数舍入，若存在两个同样接近的数，则选择偶数作为舍入值。
2. 向零舍入，又称截断舍入，将多余的精度位截掉，即取舍入后绝对值较小的值。
3. 正向舍入，也称正无穷舍入，即舍入后结果大于原值。
4. 负向舍入：也称负无穷舍入，即舍入后结果小于原值。

小结

这回终于可以解释0.1+0.2!=0.3了吧，0.3本身就无法精确的表示

也能用舍入的知识解释0.99999999999999999999999999999999999999999为什么等于1了（仅对于计算机浮点数计算）

更多细节可以查看维基百科上的IEEE754词条