『欧拉-拉格朗日方程』在控制科学中

最新推荐文章于 2024-09-10 14:59:31 发布

jiushiqy

最新推荐文章于 2024-09-10 14:59:31 发布

阅读量321

点赞数 1

文章标签：科技

本文链接：https://blog.csdn.net/jiushiqy/article/details/139168899

版权

最开始接触欧拉拉格朗日方程还是在理论力学中， $\frac{\partial L}{\partial q} - \frac{d L}{d t} \frac{\partial L}{\partial \dot{q}}= 0$ ，其中，q代表自由度，L代表能量方程，在几种不同的情况下能量方程的含义和等式右边也有所不同，如上图所示，通过该方程就可以建立系统运动微分方程，求解一系列力学问题。后来学习非线性控制时，发现也有欧拉拉格朗日方程的身影，这次是在一般形式下，从最小化代价函数的角度出发求解最优路径的问题。今天着重描述一下后者：

（后来才知道，本质上这两个都属于数学中的变分法，我以为两个不同的东西竟然能统一起来真的很神奇，但本质上他们就是同一个东西。不得不感慨，数学在工科中真的是降维打击。当然纯数学的理论我也不是很懂，欢迎各路大神批评指正！）

以下内容参考了慕尼黑工业大学Boris Lohmann 教授的现代控制理论2 讲义：

考虑如下形式的代价函数：

$J = \int_{t_{0}}^{t_{e}}g(\mathbf{x}, \mathbf{\dot{x}}, t) \stackrel{!}{=} min$

其中 $t_{0}, t_{e}, \mathbf{x_{0}}, \mathbf{x_{e}}$ 为已知，求最优的路径 $\mathbf{x}(t)$ 。

我们假设最优路径为 $\mathbf{x}^{*}(t)$ ，那么，其他有偏差的非最优路径我们可以表示为： $\mathbf{x}(t, \epsilon) = \mathbf{x}^{*}(t) + \epsilon \cdot\mathbf{\tilde{x}}(\mathbf{x})$ ,其中， $\mathbf{\tilde{x}}(\mathbf{x})$ 为变化量或者说偏差量， $\epsilon$ 是一个有正上确界的小量。很自然，当 $\epsilon$ 值为0时，轨迹为最优轨迹，在此时 $\tilde{\mathbf{x}}(t)$ 是任意的，那么我们令： $\tilde{\mathbf{x}}(t_{0}) = \mathbf{0}, \tilde{\mathbf{x}}(t_{e}) = \mathbf{0}$ ，这样，原来的初始状态和最终状态都没有发生改变。

通过以上的论述我们不难将一般化轨迹的代价函数写为一个关于 $\epsilon$ 的函数：

$J = \int_{t_{0}}^{t_{e}}g(\mathbf{x}^{*} + \epsilon\mathbf{\tilde{x}} , \mathbf{\dot{x}}^{*} + \epsilon \mathbf{\dot{\tilde{x}}}, t) = F(\epsilon)$

一般的，我们处理极值问题即是将函数求导以后令导数等于0，这里我们又预先知道为0时该代价函数最小，于是有： $\frac{d F}{d\epsilon}|_{\epsilon = 0} = 0$ 。接下来我们将等式左边展开，看看会得到什么 (以下数学过程见图片里的手动推导)

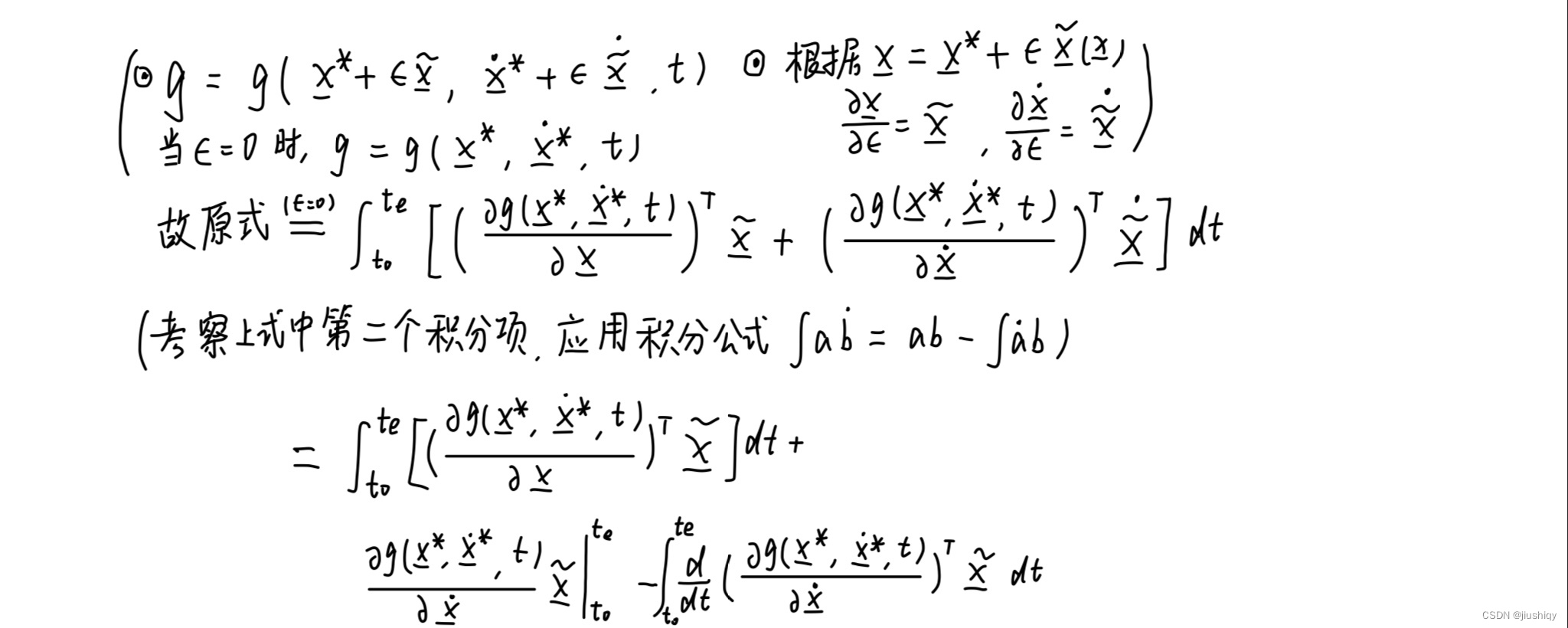
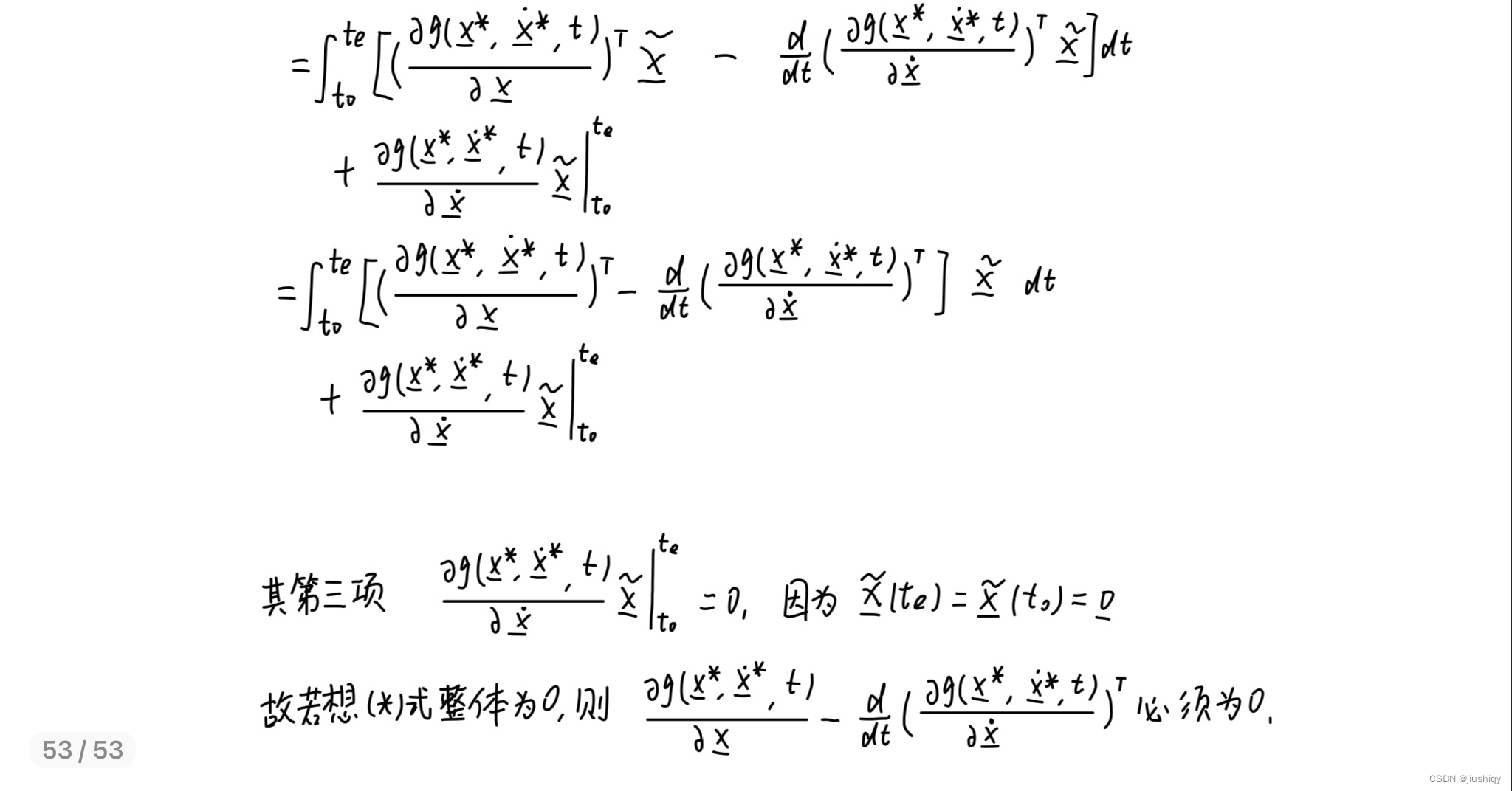
细心的同学可能已经发现了，此时我们熟悉的欧拉拉格朗日方程又一次闪亮登场：

$\frac{\partial g}{\partial \mathbf{x}} - \frac{d}{dt}\frac{\partial g}{\partial \mathbf{\dot{x}}}= \mathbf{0}$

即，当代价函数已知并满足我们上述的几个假设时，满足上面方程的轨迹即为最优轨迹。额外的，当上述假设不成立时，我们需要在这个方程的基础上增加一些条件再进行求解。后续我还会更新以下非线性控制的内容，这个方程在那里也会被频繁用到。

以上，如有不当之处，欢迎各路大神指出，并批评指正！

jiushiqy

关注

1
点赞
踩
3

收藏

觉得还不错? 一键收藏
1
评论
『欧拉-拉格朗日方程』在控制科学中

其中，q代表自由度，L代表能量方程，在几种不同的情况下能量方程的含义和等式右边也有所不同，如上图所示，通过该方程就可以建立系统运动微分方程，求解一系列力学问题。后来学习非线性控制时，发现也有欧拉拉格朗日方程的身影，这次是在。即，当代价函数已知并满足我们上述的几个假设时，满足上面方程的轨迹即为最优轨迹。额外的，当上述假设不成立时，我们需要在这个方程的基础上增加一些条件再进行求解。，我以为两个不同的东西竟然能统一起来真的很神奇，但本质上他们就是同一个东西。以上，如有不当之处，欢迎各路大神指出，并批评指正！
复制链接

扫一扫