Matlab中mldivide函数的使用

jk_101

于 2022-05-10 10:00:00 发布

阅读量2.2k

点赞数 2

分类专栏： Matlab 文章标签： matlab 矩阵线性代数

本文链接：https://blog.csdn.net/jk_101/article/details/111225370

版权

Matlab 专栏收录该内容

720 篇文章

订阅专栏

对线性方程组 Ax = B 求解 x

语法

x = A\B

x = mldivide(A,B)

说明

x = A\B对线性方程组 A*x = B 求解。矩阵 A 和 B 必须具有相同的行数。如果 A 未正确缩放或接近奇异值，MATLAB® 将会显示警告信息，但还是会执行计算。

如果 A 是标量，那么 A\B 等于 A.\B。
如果 A 是 n×n 方阵，B 是 n 行矩阵，那么 x = A\B 是方程 A*x = B 的解（如果存在解的话）。
如果 A 是矩形 m×n 矩阵，且 m ~= n，B 是 m 行矩阵，那么 A\B 返回方程组 A*x= B 的最小二乘解。

x = mldivide(A,B) 是执行 x = A\B 这一操作的替代方法，但很少使用。它可以启用类的运算符重载。

示例

方程组

对简单的线性方程组 A*x = B 求解。

A = magic(3);
B = [15; 15; 15];
x = A\B
x = 3×1

    1.0000
    1.0000
    1.0000

包含奇异矩阵的线性方程组

对包含奇异矩阵 A 的线性方程组 A*x = b 求解。

A = magic(4);
b = [34; 34; 34; 34];
x = A\b

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  4.625929e-18.

x = 4×1

    0.9804
    0.9412
    1.0588
    1.0196

如果 rcond 在 0 和 eps 之间，MATLAB® 会发出接近奇异的警告，但还会继续计算。如果处理的是病态矩阵，尽管残差 (b-A*x) 相对较小，还是有可能出现不可靠解。在此特例中，残差的范数是零，尽管rcond很小，仍能求得精确解。

当 rcond 等于0时，会出现奇异警告。

A = [1 0; 0 0];
b = [1; 1];
x = A\b

Warning: Matrix is singular to working precision.
x = 2×1

     1
   Inf

这种情况下，除以零会导致计算涉及 Inf 和/或 NaN，使得计算结果不可靠。

欠定方程组的最小二乘解

对线性方程组A*x = b求解。

A = [1 2 0; 0 4 3];
b = [8; 18];
x = A\b
x = 3×1

         0
    4.0000
    0.6667

包含稀疏矩阵的线性方程组

使用稀疏矩阵对简单的线性方程组求解。

考虑以下矩阵方程A*x = B。

A = sparse([0 2 0 1 0; 4 -1 -1 0 0; 0 0 0 3 -6; -2 0 0 0 2; 0 0 4 2 0]);
B = sparse([8; -1; -18; 8; 20]);
x = A\B
x = 
   (1,1)       1.0000
   (2,1)       2.0000
   (3,1)       3.0000
   (4,1)       4.0000
   (5,1)       5.0000

提示

运算符 / 和 \ 通过以下对应关系而相互关联：B/A = (A'\B')'。
如果 A 是方阵，则 A\B 约等于 inv(A)*B，但 MATLAB 会用不同的更为稳健的方式处理 A\B，而且效果更好。
如果 A 的秩小于 A 中的列数，则 x = A\B 不一定是最小范数解。可以使用 x =lsqminnorm(A,B) 或 x =pinv(A)*B 来计算最小范数最小二乘解。

算法

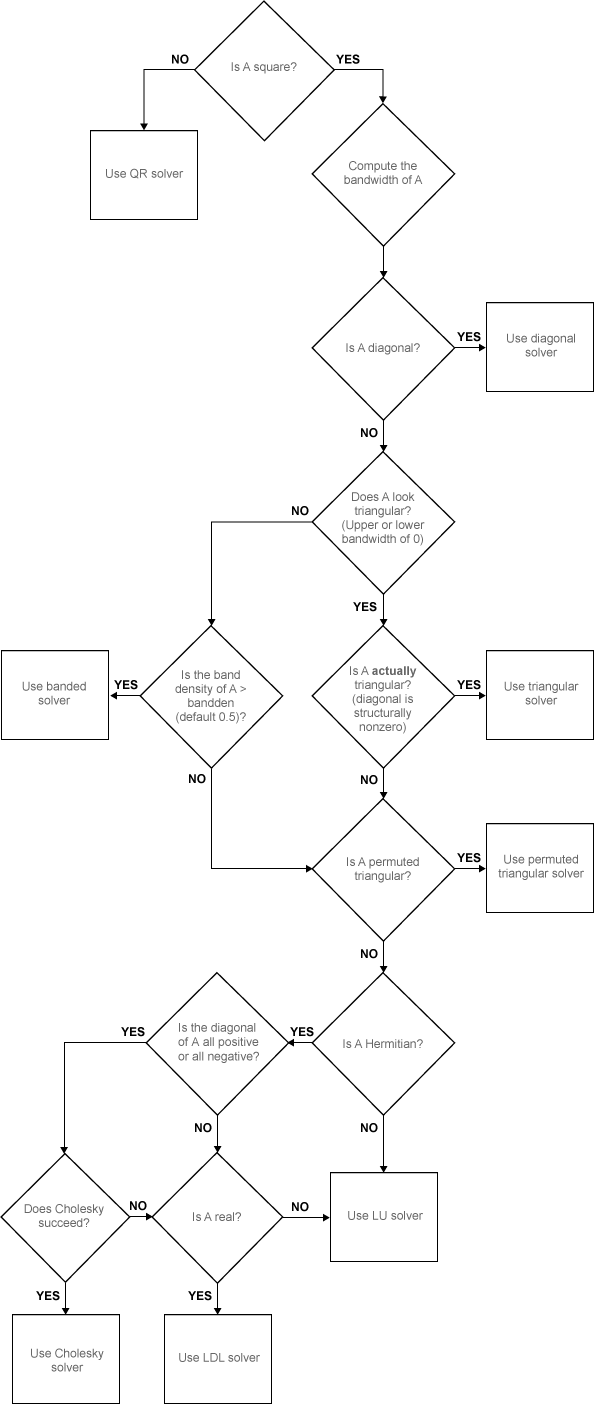
mldivide 在求解线性方程组方面的多用性源于其能够在调度适当的求解器时利用问题中的对称性。此方法旨在最大限度减少计算时间。该函数首先区分满（也称为“稠密”）和稀疏输入数组。

针对完全输入的算法

下面的流程图显示当输入 A 和 B 为完全时的算法路径。