对偶专题——Duality and Dual problem (一)

前言

对偶，是我们在最优化里面经常会遇到的一个名词，尤其是在机器学习里面，在优化模型的最后都会使用到一个对偶，比如SVM、最大熵、Fisher 鉴别都会使用到对偶；同时，在很多其他问题，例如线性规划也存在对偶问题。本人刚刚接触这东西的时候，感觉很奇妙。妙在对偶问题一般会使得优化问题变得更加容易求解，奇在 为什么对偶形式是那样子写？KKT条件又是什么鬼···

本专题就来细细的分析，对偶问题的到底是怎么回事，它其实一点都不神秘。

对偶问题

从一般问题开始说起

考虑下面一个一般的带约束的最优化问题：

我们要优化的目标函数是$f_0(x)$ ,它可以是任意的可导函数，我们的目标是最小化这个函数。

约束条件有两类：$m$ 个不等式约束,以及$p$ 个 等式约束。
假设约束条件下的$x$的定义域记为$D$ 。

本科期间，我们学习到了先通过对目标函数求偏导，然后让偏导为0，解出使得导数为0的$x^{\ast }$ 后，再反代入$f_0(x)$，得到一个可能的极值:$f_0(x^{\ast })$，然后我们再去判断这个$f_0(x^{\ast })$ 到底是极大值还是极小值，或者到底是不是极值。

然而，上面这套方法是用于无约束条件的下的方法。现在，我们面临的如何在一坨等式约束和不等式约束面前去最优化某个函数，也就是需要在$D$ 集合去最优化这个函数。

因为带约束的最优化我们不会做，我们只会做无约束的最优化。因此一个很自然的想法就是：我们能不能把约束条件去掉，使得我们要最优化的函数化归到无约束？

首先我们构造这么一个目标函数:
$H(x)=f_0(x)+{\sum }_{i=1}^{m}I\_(f_i(x))+{\sum }_{i=1}^m{I}_0(h(x))$
其中$I\_(u)$ 和$I_0(u)$ 的定义为：

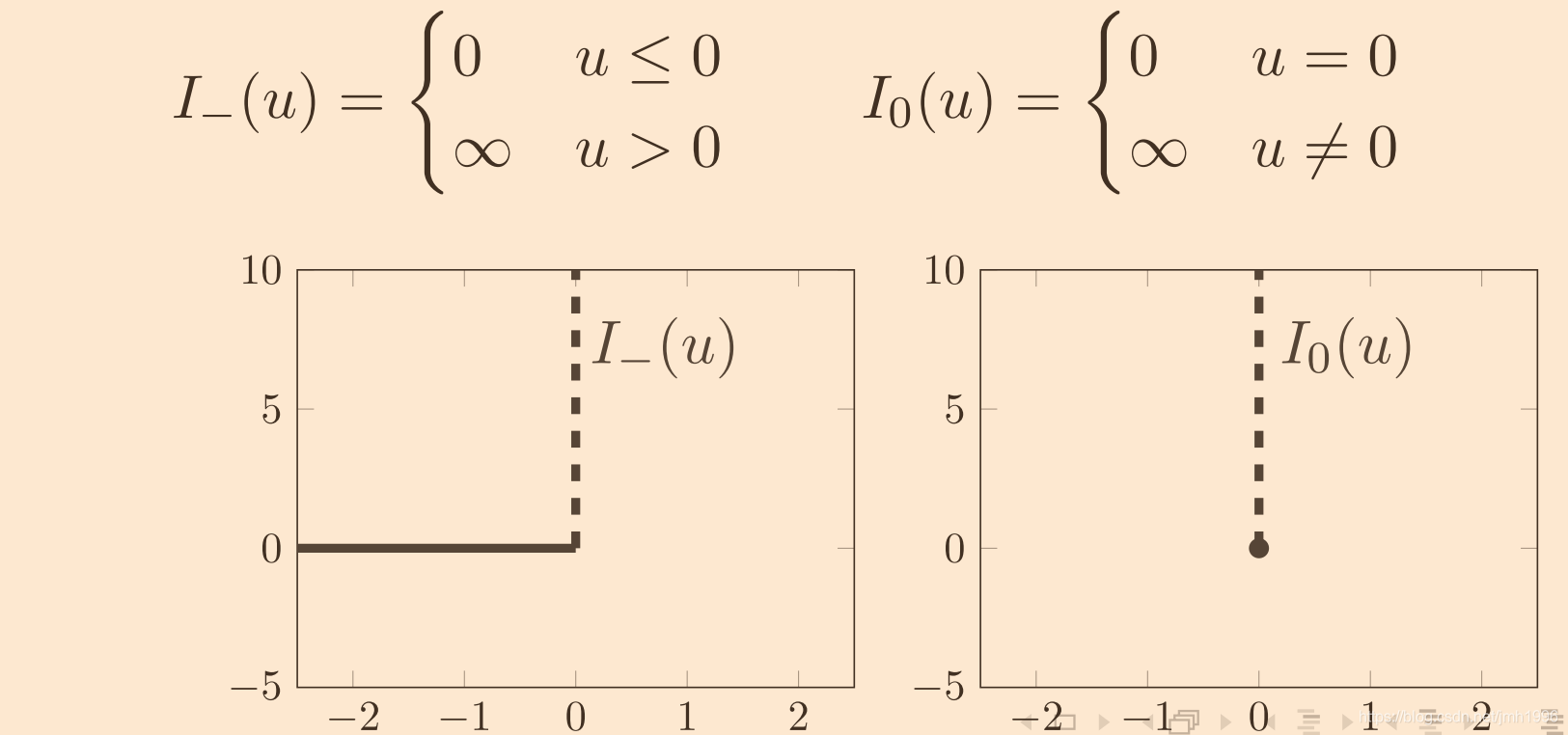
这两个函数是个栅栏函数，在$I\_(u)$在$u\le 0$的时候都是0，而在$u>0$的时候为正无穷。同样的$I_0(u)$在$u̸=0$的时候为正无穷，而在$u=0$ 的时候为0。

当我们去$min$ 最小化$H(x)$ 的时候，$x$是不带任何约束的，即$x\in R$。但是此时我们的目标是最小化，如果这个函数存在最小值，那么这个最小值肯定不会是正无穷的吧。于是在最小化$H(x)$的过程中，其实$x$的取值一定会趋向于让$I\_(f_i(x))=0$，以及$I_0(h_i(x))=0$，否则$H(x)$ 就没有最小值可言。
于是：$min$ $H(x)$ 的最优值点$x^{\ast }$ 必然会使得$I\_(f_i(x^{\ast }))=0$，以及$I_0(h_i(x^{\ast }))=0$，这也就使得$f_i(x^{\ast })\le 0$,以及$h_i(x^{\ast })=0$。这就说明了，我们构造的不带约束的最小化目标函数$H(x)$，就是等效于最小化原目标函数$f_0(x)$.

好了，现在我们已经把带约束的目标函数转换成了不带约束的目标函数。接下来，我们尝试对这个函数求导，然后把导数为0的$x^{\prime }$ 代入求最小值。但是此时，我们会发现：$H(x)$ 因为带了$I\_(f_i(x))$以及$I_0(h_i(x))$ ，使得$H(x)$ 自身是不可导的。

那这些就麻烦了，我们构造了一个不可导的函数$H(x)$，它的确不带约束了，但是不可导就甚是不好。

我们只会做不带约束的、可导的函数优化，那么我们现在的想法也自然是想办法把$H(x)$ 变成可导的咯。

我们的方法是这样的：找一个$H(x)$的简单可导下界函数 $L(x)$。注意了我们的目标是 找到 一个函数 $L(x)$，它得是$H(x)$的下界，同时对$L(x)$求导 相对于对原函数 $f_0(x)$ 求导，不会增加太多的工作量。
我们注意到，导致$H(x)$ 不可导的根源是$I\_(f(x))$ 和 $I_0(h(x))$。我们再观察一下他们的图像。

现在，我们分别找到了$I\_(u)$ 的下界$\hat{I}\_(u)=-\lambda u(\lambda \le 0)$ 和$I_0(u)$ 的下界${\hat{I}}_0(u)=-\lambda u$。可以看到对于$I\_(u)$来说，对于所有的$u\in R$，都有$I\_(u)\ge \hat{I}\_(u)$。
同理，对于$I_{(}u)$来说，任意的$u$都有${\hat{I}}_0(u)\le I_0(u)$。这是因为，对于$I_0(u)$ 来说 它只在$u=0$ 的值为0，其他值全部为真无穷，那么显然有$\mu u\le I_0(u)$。

于是，我们有$f_0(x)+{\sum }_{i=1}^m-{\lambda }_i{f}_i(x)-{\sum }_{i=1}^p{\mu }_i{h}_i(x)$ 是$H(x)$ 的下界，当然在约束条件确定的可行域下它也是原目标优化函数$f_0(x)$ 的下界。
其中${\lambda }_i\le 0$，$u_i\in R$。请体会一下，为什么${\lambda }_i$是负的，而$u_i$ 却是没有任何约束。

这一点可以从两个角度来考虑。一个是考虑到我们的目标是找到小于等于$H(x)$ 的函数$L(x)$,用两个线性函数去表示$H(x)$里面的那两个栅栏函数。于是对$I\_(u)$ 来说，我们应该构造一三象限的直线。对于$I_0(u)$来说，只要构造一个过原点的直线即可。于是${\lambda }_i$和$u_i$就是反映我们选择了那个线性函数的形状。

另外一点，直接从原目标函数$f_0(x)$ 出发，结合约束条件寻找它的一个下界函数：$f_0(x)+{\sum }_{i=1}^m-{\lambda }_i{f}_i(x)-{\sum }_{i=1}^p{\mu }_i{h}_i(x)$。既然要是$f_0(x)$的下界，那当然是需要从$-{\lambda }_i{f}_i(x)$减去一部分内容了才能更小了。而对于原来的满足条件的$x^{\ast }$而言 $f_i(x^{\ast })\le 0$,$h_i(x^{\ast })=0$。所以 $-{\lambda }_i{f}_i(x)$小于0，配上$f_i(x)\le 0$.有${\lambda }_i$也要小于等于0。

现在我们已经有了$L(x)$,它其实带着参数${\lambda }_i和u_i$的，它是$H(x)$的下界，于是它又可以写成$L(x,\lambda ,u)$。可是当知道个下界还不得行，因为为什么呢？下界如果离目标函数相差太远，举个极端的例子来说，如何下界函数是负无穷的话，它也是下界，但是它就没有给我们的原问题提供任何有意义的信息。因为我们想让这个下界函数是很靠近$f_0(x)$。

怎么做呢？先求$L(x,\lambda ,u)$的最小值，消去$x$ 得到$L(x,\lambda ,u)$ 的下确界函数，它应该是关于$\lambda ,u$的函数。然后，我们让这个下确界最大，就能得到离原函数特别接近的一个函数值。

这么做的原理是这样子的：因为对于任意的 $x\in D$ ,我们构造的$L(x,\lambda ,u)$ 是小于等于$f_0(x)$ 的。$L(x,\lambda ,u)$与$f_0(x)$的关系有点类似于下面这个图。

这个图的做法是，先给定$x$，计算$f_0(x)$ 和 $L(x,\lambda ,u)$。这个时候$f_0(x)$会得到一个数值，但是$L(x,\lambda ,u)$却得到一个关于$\lambda ,u$的函数$G(\lambda ,u)$ ,没关系，我们可以求这个函数$G(\lambda ,u)$ 的最大值$G^{\prime }(\lambda ,u)$，得到一个确定的数值。这个在定义域$D$ 遍历所有的$x$ ，得到对应的$f_0(x)$ 和$maxL(x,\lambda ,u)$ 就可以得到这个图像了。

从这个图可以看出，1.$L(x,\lambda ,u)$ 的全局最大值就是最接近$f_0(x)$最小值的地方。
2.原函数$f_0(x)$可能是个非凸的复杂函数，但是它对应的$L(x,\lambda ,u)$在给定$x$ 下的最大值却是一个凸函数，有全局最优。

于是，我们的目标就是转而计算$L(x,\lambda ,u)$的最大值。这种计算，一般是这么实施：先计算固定$\lambda ,u$,计算$L(x,\lambda ,u)$关于$x$ 的最小值；然后在变化$\lambda ,u$ 使得这个最小值最大。
我们形式化的写出来就是：

1. 先定义一个$f_0(x)$ 的下界函数$L(x,\lambda ,u)$
2. 求$L(x,\lambda ,u)$的下确界${\inf }_{x\in D}L(x,\lambda ,u)$
3. 让 ${\inf }_{x\in D}L(x,\lambda ,u)$ 最大。
   这个过程中的最大化 ${\inf }_{x\in D}L(x,\lambda ,u)$就是所谓的拉格朗日问题。

举个小栗子

假设，我们现在要求解下面这个最优化问题：

目标的函数图像是这样的：

通过数形结合，我们晓得目标函数是在$x=1$的地方取得最小值，而$x=1$ 也刚好满足约束条件： D = { x ∣ − x ≤ 0 } D=\{x|-x\leq 0\} D={x∣−x≤0}。
现在，我们记原目标函数为$f(x)=x^2-2x$，然后 我们构造这么一个函数
$p(x)=x^2-2x+I\_(x)$，这个函数不受任何约束，它的定义域是$R$。

其中$I\_(u)$定义是：$如果u\le 0,I_1(u)=0;否则I_1(u)=+\infty$。它的图像是：

对于任何属于$D$ 的 $x$,即$-x\le 0$，有$f(x)=p(x)$；当$-x>0$ 时，$p(x)=+\infty$。

假设原问题的最优解在$x^{\ast }$ 取得，那么必然有$f(x^{\ast })=p(x^{\ast })$。同时当我们最小化$p(x)$的时候，$p(x)$ 最小值 当然也只能在$x^{\ast }$取得。

但$I\_(x)$ 不是一个可导的函数，我们希望能够把找到一个简单的可导的函数来“近似”它，就算不能近似如果能表示它的下界也好。

我们用$\hat{I}\_(x)=-\lambda x,\lambda \le 0$ 这么一个简单的线性函数来近似$I\_(x)$。

虽然$\hat{I}\_(x)$ 和$I\_(x)$ 相差不挺大的，但是没有关系，最起码这个函数能够保证$\forall x\in R,\hat{I}\_(x)\le I\_(x)$，换句话说 我们找到了$I\_(x)$的一个性质优良的下界函数。

现在，我们用$\hat{I}\_(x)$ 替换到$p(x)$里面的$I\_(x)$.得到：$f(x)+(-\lambda (-x))=x^2-2x+\lambda x$,其中$\lambda \le 0$ 。

我们把这个含有$\lambda$ 的函数记做$L(x,\lambda )=f(x)+\hat{I}\_(x)=x^2-2x+\lambda x$

我们知道在最小值处 $f(x)\ge p(x)\ge L(\lambda ,x)$.
OK,现在我们来求$L(x,\lambda )$ 的下界函数 $g(\lambda )={\inf }_{x\in R}L(\lambda ,x)$，下界函数是关于$\lambda$ 的函数。
$g(\lambda )$的求法如下：
求$\frac{\partial L(x,\lambda )}{\partial x}，得到\frac{\partial L(x,\lambda )}{\partial x}=2x-2+\lambda$。

令$\frac{\partial L(x,\lambda )}{\partial x}=0$，得到$2x-2+\lambda =0$，于是$x=\frac{2-\lambda }{2}$.

求$\frac{\partial \frac{\partial L}{\partial x}}{\partial x}=2>0$，因此把$x=\frac{2-\lambda }{2}$ 代入$L(x,\lambda )$可以得到$L$的下界。

此时$L(\frac{2-\lambda }{2},\lambda )=(\frac{2-\lambda }{2}{)}^2-2(\frac{2-\lambda }{2})+\lambda \frac{2-\lambda }{2}=\frac{2-\lambda }{2}(\frac{2-\lambda }{2}-2+\lambda )=\frac{2-\lambda }{2}(\frac{2-\lambda -4+2\lambda }{2})=(\frac{2-\lambda }{2})(\frac{\lambda -2}{2})=\frac{-1}{4}(\lambda -2{)}^2$

所以$g(\lambda )=\frac{-1}{4}(\lambda -2{)}^2$,其中$\lambda \le 0$。
$g(\lambda )$的最大值$maxg(\lambda )=-1$。

刚好拿到了和原函数$f_0(x)$一样的最优值$-1$。

OK,下篇博客就介绍，什么时候两个函数得到的最优值的是一样的，这就是成为的KKT条件。