1.预备知识
2.提升树
被认为是统计学习中性能最好的方法之一
2.1 一般步骤
2.1.1 模型
使用的也是加法模型: f M ( x ) = ∑ m = 1 M T ( x ; Θ m ) f_M(x)=\sum_{m=1}^MT(x;\Theta_m) fM(x)=m=1∑MT(x;Θm),其中 M M M为树的个数, T ( x ; Θ m ) T(x;\Theta_m) T(x;Θm)表示决策树, Θ m \Theta_m Θm为决策树的参数。
2.1.2 损失函数
- 回归问题:平方误差损失函数
- 分类问题:
- 二分类问题:指数损失函数
- 多分类问题:softmax
- 一般决策问题:自定义损失函数
2.1.3 优化方法
前向分步算法:
如书上:
其中当前模型
f
m
(
x
)
f_m(x)
fm(x)已知。
2.2 二分类问题的提升树
2.2.1 基学习器
CART决策树
2.2.2 损失函数
使用指数损失函数: f ( x ) = ∑ m = 1 M β m b ( x ; γ m ) f M ( x ) = ∑ m = 1 M T ( x ; Θ m ) f(x)=\sum_{m=1}^M\beta_mb(x;\gamma _m)\\f_M(x)=\sum_{m=1}^MT(x;\Theta_m) f(x)=m=1∑Mβmb(x;γm)fM(x)=m=1∑MT(x;Θm)
2.2.3 说明
提升树相当于Adaboost算法的特殊情况,
Adaboost的模型为: f ( x ) = ∑ m = 1 M α m G m ( x ) = α 1 G 1 ( x ) + ⋯ + α m G m ( x ) + ⋯ + α M G M ( x ) \begin{aligned}f(x)&=\sum_{m=1}^M\alpha_m G_m(x)\\&=\alpha_1G_1(x)+\cdots+\alpha_mG_m(x)+\cdots+\alpha_MG_M(x)\end{aligned} f(x)=m=1∑MαmGm(x)=α1G1(x)+⋯+αmGm(x)+⋯+αMGM(x),其中 α m \alpha_m αm由 G m ( x ) G_m(x) Gm(x)的"分类误差率"决定,训练样本 G m ( x ) G_m(x) Gm(x):提高前一轮“错误分类”的样本的权值,降低前一轮“正确分类”的样本的权值。
它只是将:
- 1.基分类器G(x)限制为二分类树;
- 2.基分类器权重
α
m
\alpha_m
αm全部置为1。
如图:
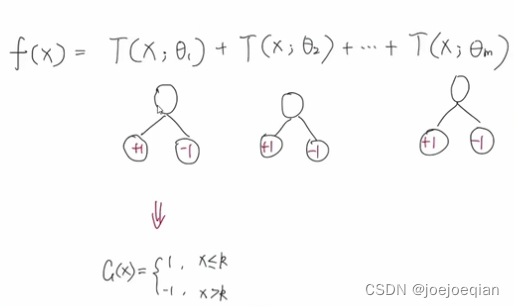
2.2.4 原理
只要我们使用的是指数损失函数,就可以用指数损失函数来调整样本数据的权重,从而让每个基分类器学到不同的内容。
指数损失函数:
L ( y , f ( x ) ) = exp [ − y f ( x ) ] L(y,f(x))=\exp[-yf(x)] L(y,f(x))=exp[−yf(x)]
,其中当 f ( x ) f(x) f(x)分类正确时,与 y y y同号, L ( y , f ( x ) ) < = 1 L(y,f(x))<=1 L(y,f(x))<=1。当 f ( x ) f(x) f(x)分类错误时,与 y y y异号, L ( y , f ( x ) ) > 1 L(y,f(x))>1 L(y,f(x))>1。
2.3 回归问题的提升树
2.3.1 基学习器
CART回归树
T
(
x
;
Θ
)
=
∑
j
=
1
J
c
j
I
(
x
∈
R
j
)
T(x;\Theta)=\sum_{j=1}^Jc_jI(x\in R_j)
T(x;Θ)=∑j=1JcjI(x∈Rj)
f
M
(
x
)
=
∑
m
=
1
M
T
(
x
;
Θ
m
)
f_M(x)=\sum_{m=1}^MT(x;\Theta_m)
fM(x)=∑m=1MT(x;Θm)
2.3.2 损失函数
使用平方误差损失:
L
(
y
,
f
(
x
)
)
=
(
y
−
f
(
x
)
)
2
L(y,f(x))=(y-f(x))^2
L(y,f(x))=(y−f(x))2
L
(
y
,
f
(
x
)
)
=
(
y
−
f
(
x
)
)
2
=
[
y
−
f
m
−
1
(
x
)
−
T
(
x
;
Θ
m
)
]
2
=
[
r
−
T
(
x
;
Θ
m
)
]
2
\begin{aligned}L(y,f(x))&=(y-f(x))^2\\&=[y-f_{m-1}(x)-T(x;\Theta_m)]^2\\&=[r-T(x;\Theta_m)]^2\end{aligned}
L(y,f(x))=(y−f(x))2=[y−fm−1(x)−T(x;Θm)]2=[r−T(x;Θm)]2
,其中
r
r
r是残差,目标就是拟合残差
r
r
r。
2.3.3 前向分步算法
θ ^ m = arg min θ m ∑ i = 1 N L ( y ( i ) , f m − 1 ( x ( i ) ) + T ( x ( i ) , θ m ) ) = arg min θ m ∑ i = 1 N ( r m ( i ) − T ( x ( i ) , θ m ) ) 2 \begin{aligned}\hat\theta_m&=\arg\min_{\theta m}\sum_{i=1}^NL(y^{(i)},f_{m-1}(x^{(i)})+T(x^{(i)},\theta_m))\\&=\arg\min_{\theta m}\sum_{i=1}^N(r_m^{(i)}-T(x^{(i)},\theta_m))^2\end{aligned} θ^m=argθmmini=1∑NL(y(i),fm−1(x(i))+T(x(i),θm))=argθmmini=1∑N(rm(i)−T(x(i),θm))2
2.3.4 思路
1.个体学习器如何训练得到
如何改变训练数据的权值或概率分布如何改变?
用残差进行拟合,一步一步的将残差缩小。
2.如何将个体学习器组合
相加
3.目标
- 使得总体损失逐步减少

3.一般决策问题梯度提升树GBDT
GBDT也是迭代,使用了前向分布算法,但是弱学习器限定了只能使用CART回归树模型,同时迭代思路和Adaboost也有所不同。
GBDT的思想可以用一个通俗的例子解释,假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。
从上面的例子看这个思想还是蛮简单的,但是有个问题是这个损失的拟合不好度量,损失函数各种各样,怎么找到一种通用的拟合方法呢?
3.1 要解决的问题

3.2 基学习器
回归树:
T
(
x
;
Θ
)
=
∑
j
=
1
J
c
j
I
(
x
∈
R
j
)
T(x;\Theta)=\sum_{j=1}^Jc_jI(x\in R_j)
T(x;Θ)=∑j=1JcjI(x∈Rj)
f
M
(
x
)
=
∑
m
=
1
M
T
(
x
;
Θ
m
)
f_M(x)=\sum_{m=1}^MT(x;\Theta_m)
fM(x)=∑m=1MT(x;Θm)
3.3 损失函数
找到一般的损失函数: L ( y , f ( x ) ) L(y,f(x)) L(y,f(x))
3.4 前向分步算法+梯度提升
3.4.1 核心目标
1.已知加法模型,一定会存在多个优化器,不断迭代优化;
2.我们要确保,每增加一个基学习器,都要使得总体损失越来越小,即第m步要比第m-1步的损失要小。
即:
L
(
y
(
i
)
,
f
m
(
x
(
i
)
)
)
<
L
(
y
(
i
)
,
f
m
−
1
(
x
(
i
)
)
)
→
L
(
y
(
i
)
,
f
m
−
1
(
x
(
i
)
)
)
−
L
(
y
(
i
)
,
f
m
(
x
(
i
)
)
)
>
0
\begin{aligned}&L(y^{(i)},f_m(x^{(i)}))<L(y^{(i)},f_{m-1}(x^{(i)}))\rightarrow L(y^{(i)},f_{m-1}(x^{(i)}))-L(y^{(i)},f_m(x^{(i)}))>0\end{aligned}
L(y(i),fm(x(i)))<L(y(i),fm−1(x(i)))→L(y(i),fm−1(x(i)))−L(y(i),fm(x(i)))>0
3.4.2 将损失函数进行处理
处理的原因就是:往我们的核心目标上靠。
L ( y ( i ) , f m ( x ( i ) ) ) < L ( y ( i ) , f m − 1 ( x ( i ) ) ) → L ( y ( i ) , f m − 1 ( x ( i ) ) ) − L ( y ( i ) , f m ( x ( i ) ) ) > 0 \begin{aligned}&L(y^{(i)},f_m(x^{(i)}))<L(y^{(i)},f_{m-1}(x^{(i)}))\rightarrow L(y^{(i)},f_{m-1}(x^{(i)}))-L(y^{(i)},f_m(x^{(i)}))>0\end{aligned} L(y(i),fm(x(i)))<L(y(i),fm−1(x(i)))→L(y(i),fm−1(x(i)))−L(y(i),fm(x(i)))>0
由泰勒公式: f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x)\approx f(x_0)+f^{'}(x_0)(x-x_0) f(x)≈f(x0)+f′(x0)(x−x0)和 L ( y , f m ( x ) ) L(y,f_m(x)) L(y,fm(x))中只有 f m ( x ) f_m(x) fm(x)是未知量,且 f m ( x ) = f m − 1 ( x ) + T ( x ; Θ m ) f_m(x)=f_{m-1}(x)+T(x;\Theta_m) fm(x)=fm−1(x)+T(x;Θm),得:
L ( y , f m ( x ) ) ≈ L ( y , f m − 1 ( x ) ) + ∂ L ( y , f m ( x ) ) ∂ f m ( x ) ∣ f m ( x ) = f m − 1 ( x ) ⋅ ( f m ( x ) − f m − 1 ( x ) ) = L ( y , f m − 1 ( x ) ) + ∂ L ( y , f m ( x ) ) ∂ f m ( x ) ∣ f m ( x ) = f m − 1 ( x ) ⋅ T ( x ; Θ m ) \begin{aligned}L(y,f_m(x))&\approx L(y,f_{m-1}(x))+\frac{\partial L(y,f_m(x))}{\partial f_m(x)}|_{f_m(x)=f_{m-1}(x)}\cdot \left(f_m(x)-f_{m-1}(x)\right)\\& = L(y,f_{m-1}(x))+\frac{\partial L(y,f_m(x))}{\partial f_m(x)}|_{f_m(x)=f_{m-1}(x)}\cdot T(x;\Theta_m)\end{aligned} L(y,fm(x))≈L(y,fm−1(x))+∂fm(x)∂L(y,fm(x))∣fm(x)=fm−1(x)⋅(fm(x)−fm−1(x))=L(y,fm−1(x))+∂fm(x)∂L(y,fm(x))∣fm(x)=fm−1(x)⋅T(x;Θm)
即有:
L ( y , f m − 1 ( x ) ) − L ( y , f m ( x ) ) ≈ − ∂ L ( y , f m ( x ) ) ∂ f m ( x ) ∣ f m ( x ) = f m − 1 ( x ) ⋅ T ( x ; Θ m ) \begin{aligned}L(y,f_{m-1}(x))-L(y,f_m(x))&\approx -\frac{\partial L(y,f_m(x))}{\partial f_m(x)}|_{f_m(x)=f_{m-1}(x)}\cdot T(x;\Theta_m)\end{aligned} L(y,fm−1(x))−L(y,fm(x))≈−∂fm(x)∂L(y,fm(x))∣fm(x)=fm−1(x)⋅T(x;Θm)
当
T
(
x
;
Θ
m
)
≈
−
∂
L
(
y
,
f
m
(
x
)
)
∂
f
m
(
x
)
∣
f
m
(
x
)
=
f
m
−
1
(
x
)
T(x;\Theta_m)\approx -\frac{\partial L(y,f_m(x))}{\partial f_m(x)}|_{f_m(x)=f_{m-1}(x)}
T(x;Θm)≈−∂fm(x)∂L(y,fm(x))∣fm(x)=fm−1(x)时,
L
(
y
,
f
m
−
1
(
x
)
)
−
L
(
y
,
f
m
(
x
)
)
≥
0
L(y,f_{m-1}(x))-L(y,f_m(x))\geq 0
L(y,fm−1(x))−L(y,fm(x))≥0
,其中该式子一旦等于0就终止训练。
r m ( x , y ) = − ∂ L ( y , f m ( x ) ) ∂ f m ( x ) ∣ f m ( x ) = f m − 1 ( x ) r_m(x,y)=-\frac{\partial L(y,f_m(x))}{\partial f_m(x)}|_{f_m(x)=f_{m-1}(x)} rm(x,y)=−∂fm(x)∂L(y,fm(x))∣fm(x)=fm−1(x),将 ( x i , y i ) (x_i,y_i) (xi,yi)代入 r m ( x , y ) r_m(x,y) rm(x,y),即可得到 r m r_m rm,进而得到第 m m m轮的训练数据集: T m = { ( x 1 , r m 1 ) , ( x 2 , r m 2 ) , ⋯ , ( x N , r m N ) } T_m=\{(x_1,r_{m1}),(x_2,r_{m2}),\cdots,(x_N,r_{mN})\} Tm={(x1,rm1),(x2,rm2),⋯,(xN,rmN)},其中 r m r_m rm是被划分的输入空间, c m c_m cm空间 r m r_m rm对应的输出值。
3.4.3 梯度提升
1.计算当前损失函数的负梯度表达式
r
m
(
x
,
y
)
=
−
∂
L
(
y
,
f
m
(
x
)
)
∂
f
m
(
x
)
∣
f
m
(
x
)
=
f
m
−
1
(
x
)
r_m(x,y)=-\frac{\partial L(y,f_m(x))}{\partial f_m(x)}|_{f_m(x)=f_{m-1}(x)}
rm(x,y)=−∂fm(x)∂L(y,fm(x))∣fm(x)=fm−1(x)
2.构造新的训练样本
将
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi)代入
r
m
(
x
,
y
)
r_m(x,y)
rm(x,y),即可得到
r
m
r_m
rm,进而得到第
m
m
m轮的训练数据集:
T
m
=
{
(
x
1
,
r
m
1
)
,
(
x
2
,
r
m
2
)
,
⋯
,
(
x
N
,
r
m
N
)
}
T_m=\{(x_1,r_{m1}),(x_2,r_{m2}),\cdots,(x_N,r_{mN})\}
Tm={(x1,rm1),(x2,rm2),⋯,(xN,rmN)},其中
r
m
r_m
rm是被划分的输入空间,
c
m
c_m
cm空间
r
m
r_m
rm对应的输出值。
3.让当前的基学习器去拟合上述训练样本,得到 T ( x ; Θ m ) T(x;\Theta_m) T(x;Θm)
3.5 算法流程
输入是训练集样本
T
=
{
(
x
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
(
x
m
,
y
m
)
}
T=\{(x_,y_1),(x_2,y_2), ...(x_m,y_m)\}
T={(x,y1),(x2,y2),...(xm,ym)}, 最大迭代次数T, 损失函数L。
输出是强学习器
f
(
x
)
f(x)
f(x)
- 初始化弱学习器 f 0 ( x ) = a r g m i n ⏟ c ∑ i = 1 m L ( y i , c ) f_0(x) = \underbrace{arg\; min}_{c}\sum\limits_{i=1}^{m}L(y_i, c) f0(x)=c argmini=1∑mL(yi,c)
- 对迭代轮数t=1,2,…T有:
a) 对样本 i = 1 , 2 , ⋯ , m i=1,2,\cdots,m i=1,2,⋯,m,计算负梯度 r t i = − [ ∂ L ( y i , f ( x i ) ) ) ∂ f ( x i ) ] f ( x ) = f t − 1 ( x ) \begin{aligned}r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1} (x)}\end{aligned} rti=−[∂f(xi)∂L(yi,f(xi)))]f(x)=ft−1(x)
b) 利用 ( x i , r t i ) ( i = 1 , 2 , . . m ) (x_i,r_{ti})(i=1,2,..m) (xi,rti)(i=1,2,..m), 拟合一棵CART回归树,得到第t颗回归树,其对应的叶子节点区域为 R t j , j = 1 , 2 , . . . , J R_{tj}, j =1,2,..., J Rtj,j=1,2,...,J。其中J为回归树t的叶子节点的个数。
c) 对叶子区域j =1,2,…J,计算最佳拟合值 c t j = a r g m i n ⏟ c ∑ x i ∈ R t j L ( y i , f t − 1 ( x i ) + c ) c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c) ctj=c argminxi∈Rtj∑L(yi,ft−1(xi)+c)
d) 更新强学习器 f t ( x ) = f t − 1 ( x ) + ∑ j = 1 J c t j I ( x ∈ R t j ) f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj}) ft(x)=ft−1(x)+j=1∑JctjI(x∈Rtj) - 得到强学习器f(x)的表达式
f
(
x
)
=
f
T
(
x
)
=
f
0
(
x
)
+
∑
t
=
1
T
∑
j
=
1
J
c
t
j
I
(
x
∈
R
t
j
)
f(x) = f_T(x) =f_0(x) + \sum\limits_{t=1}^{T}\sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})
f(x)=fT(x)=f0(x)+t=1∑Tj=1∑JctjI(x∈Rtj)

对(1)初始化的说明:
f 0 ( x ) = arg min c ∑ i = 1 N L ( y i , c ) f_0(x)=\arg\min_c\sum_{i=1}^NL(y_i,c) f0(x)=argminc∑i=1NL(yi,c)
假设L且MSE,对它求导:
∂ ∑ i = 1 N ( y i − c ) 2 ∂ c = ∑ i = 1 N − 2 ( y i − c ) = ∑ i = 1 N ( 2 c − 2 y i ) = 2 N ⋅ c − 2 ∑ i = 1 N y i \begin{aligned}\frac{\partial \sum_{i=1}^N(y_i-c)^2}{\partial c}&=\sum_{i=1}^N-2(y_i-c)\\&=\sum_{i=1}^N(2c-2y_i)\\&=2N\cdot c-2\sum_{i=1}^Ny_i\end{aligned} ∂c∂∑i=1N(yi−c)2=i=1∑N−2(yi−c)=i=1∑N(2c−2yi)=2N⋅c−2i=1∑Nyi
令 2 N ⋅ c − 2 ∑ i = 1 N y i = 0 → c = 1 N ∑ i = 1 N y i 2N\cdot c-2\sum_{i=1}^Ny_i=0\rightarrow c=\frac{1}{N}\sum_{i=1}^Ny_i 2N⋅c−2∑i=1Nyi=0→c=N1∑i=1Nyi。
3.6 思路
3.6.1 个体学习器如何训练得到
改变训练数据的权值或者概率分布,如何改变?
拟合负梯度
3.6.2 如何将个体学习组合
简单组合
3.6.3 目标
L
(
y
(
i
)
,
f
m
(
x
(
i
)
)
)
<
L
(
y
(
i
)
,
f
m
−
1
(
x
(
i
)
)
)
→
L
(
y
(
i
)
,
f
m
−
1
(
x
(
i
)
)
)
−
L
(
y
(
i
)
,
f
m
(
x
(
i
)
)
)
>
0
\begin{aligned}&L(y^{(i)},f_m(x^{(i)}))<L(y^{(i)},f_{m-1}(x^{(i)}))\rightarrow L(y^{(i)},f_{m-1}(x^{(i)}))-L(y^{(i)},f_m(x^{(i)}))>0\end{aligned}
L(y(i),fm(x(i)))<L(y(i),fm−1(x(i)))→L(y(i),fm−1(x(i)))−L(y(i),fm(x(i)))>0
使得总体损失逐步减小
3.7 例题
L = 1 2 ( y − f m ( x ) ) 2 L=\frac{1}{2}(y-f_m(x))^2 L=21(y−fm(x))2
求负梯度: − ∂ L ∂ f m ( x ) = y − f m ( x ) = r m -\frac{\partial L}{\partial f_m(x)}=y-f_m(x)=r_m −∂fm(x)∂L=y−fm(x)=rm
θ ^ m = arg min θ m ∑ i = 1 N L ( y ( i ) , f m − 1 ( x ( i ) ) + T ( x ( i ) , θ m ) ) = arg min θ m ∑ i = 1 N ( r m ( i ) − T ( x ( i ) , θ m ) ) \begin{aligned}\hat\theta_m&=\arg\min_{\theta m}\sum_{i=1}^NL(y^{(i)},f_{m-1}(x^{(i)})+T(x^{(i)},\theta_m))\\&=\arg\min_{\theta m}\sum_{i=1}^N(r_m^{(i)}-T(x^{(i)},\theta_m))\end{aligned} θ^m=argθmmini=1∑NL(y(i),fm−1(x(i))+T(x(i),θm))=argθmmini=1∑N(rm(i)−T(x(i),θm))
3.8 GBDT的优缺点
3.8.1 GBDT主要的优点
-
1.可以灵活处理各种类型的数据,包括连续值和离散值。
-
2.在相对少的调参时间情况下,预测的准确率也可以比较高。这个是相对SVM来说的。
-
3.使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
3.8.2 GBDT的主要缺点
- 1.由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
4.GBDT解决二分类问题
4.1 面临的问题
GBDT使用基分类器是回归树,其加法模型无法直接输出类别或者概率预估。
4.2 解决方案
4.2.1 逻辑回归做二分类
以往直接用逻辑回归做二分类问题时的解决方案就是用一个sigmoid函数,将输出映射到0-1的概率空间:
Z = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = w x + b y ^ = 1 1 + e − Z J = − 1 m ∑ i = 1 m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) log ( 1 − y ( i ) ) ] , 交叉熵 Z=w_1x_1+w_2x_2+\cdots+w_nx_n+b=wx+b\\\hat y = \frac{1}{1+e^{-Z}}\\J=-\frac{1}{m}\sum_{i=1}^m \left[y^{(i)}\log \hat y^{(i)}+(1-y^{(i)}\log(1-y^{(i)})\right],交叉熵 Z=w1x1+w2x2+⋯+wnxn+b=wx+by^=1+e−Z1J=−m1i=1∑m[y(i)logy^(i)+(1−y(i)log(1−y(i))],交叉熵
4.2.2 学传统逻辑回归的解决方案
通过sigmoid函数,将加法模型f(x)映射到0~1的概率空间:
模仿线性模型(交叉熵损失): f m ( x ) = ∑ m = 1 M T ( x ; Θ m ) y ^ = 1 1 + e − f m ( x ) J = − 1 m ∑ i = 1 m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) log ( 1 − y ( i ) ) ] f_m(x)=\sum_{m=1}^M T(x;\Theta_m)\\ \hat y= \frac{1}{1+e^{-f_m(x)}}\\J=-\frac{1}{m}\sum_{i=1}^m \left[y^{(i)}\log \hat y^{(i)}+(1-y^{(i)}\log(1-y^{(i)})\right] fm(x)=m=1∑MT(x;Θm)y^=1+e−fm(x)1J=−m1i=1∑m[y(i)logy^(i)+(1−y(i)log(1−y(i))]
4.3 模型
使用加法模型:
T
(
x
;
Θ
)
=
∑
j
=
1
J
c
j
I
(
x
∈
R
j
)
f
M
(
x
)
=
∑
m
=
1
M
T
(
x
;
Θ
m
)
T(x;\Theta)=\sum_{j=1}^Jc_jI(x\in R_j)\\f_M(x)=\sum_{m=1}^MT(x;\Theta_m)
T(x;Θ)=j=1∑JcjI(x∈Rj)fM(x)=m=1∑MT(x;Θm)
,其中
T
T
T前面有时有一个学习率当系数,是为了解决过拟合。
4.4 基学习器
真实值
y
y
y与整个加法模型的损失,所以要将交叉熵公式转化为
y
y
y和
f
m
(
x
)
f_m(x)
fm(x),这也是因为残差是损失函数的负梯度。
最终的损失如下:
L
(
y
,
f
m
(
x
)
)
=
log
(
1
+
e
−
f
m
(
x
)
)
+
(
1
−
y
)
⋅
f
m
(
x
)
L(y,f_m(x))=\log(1+e^{-f_m(x)})+(1-y)\cdot f_m(x)
L(y,fm(x))=log(1+e−fm(x))+(1−y)⋅fm(x)
推导过程:
y
^
=
1
1
+
e
−
f
m
(
x
)
\hat y= \frac{1}{1+e^{-f_m(x)}}
y^=1+e−fm(x)1
L = − y log y ^ − ( 1 − y ) log ( 1 − y ^ ) = − y log 1 1 + e − f m ( x ) − ( 1 − y ) log ( 1 − 1 1 + e − f m ( x ) ) = y log ( 1 + e − f m ( x ) ) − ( 1 − y ) [ log e − f m ( x ) − log ( 1 + e − f m ( x ) ) ] = y log ( 1 + e − f m ( x ) ) − ( 1 − y ) [ − f m ( x ) − log ( 1 + e − f m ( x ) ) ] = y log ( 1 + e − f m ( x ) ) + ( 1 − y ) f m ( x ) + ( 1 − y ) log ( 1 + e − f m ( x ) ) = log ( 1 + e − f m ( x ) ) + ( 1 − y ) f m ( x ) \begin{aligned}L&=-y\log\hat y-(1-y)\log(1-\hat y)\\&=-y\log\frac{1}{1+e^{-f_m(x)}}-(1-y)\log\left(1-\frac{1}{1+e^{-f_m(x)}}\right)\\&=y\log\left(1+e^{-f_m(x)}\right)-(1-y)\left[\log e^{-f_m(x)}-\log(1+e^{-f_m(x)})\right]\\&=y\log\left(1+e^{-f_m(x)}\right)-(1-y)\left[-f_m(x)-\log(1+e^{-f_m(x)})\right]\\&=y\log\left(1+e^{-f_m(x)}\right)+(1-y)f_m(x)+(1-y)\log(1+e^{-f_m(x)})\\&=\log(1+e^{-f_m(x)})+(1-y)f_m(x)\end{aligned} L=−ylogy^−(1−y)log(1−y^)=−ylog1+e−fm(x)1−(1−y)log(1−1+e−fm(x)1)=ylog(1+e−fm(x))−(1−y)[loge−fm(x)−log(1+e−fm(x))]=ylog(1+e−fm(x))−(1−y)[−fm(x)−log(1+e−fm(x))]=ylog(1+e−fm(x))+(1−y)fm(x)+(1−y)log(1+e−fm(x))=log(1+e−fm(x))+(1−y)fm(x)
4.4.1 前向分步算法+梯度提升
1.核心目标
L
(
y
(
i
)
,
f
m
(
x
(
i
)
)
)
<
L
(
y
(
i
)
,
f
m
−
1
(
x
(
i
)
)
)
→
L
(
y
(
i
)
,
f
m
−
1
(
x
(
i
)
)
)
−
L
(
y
(
i
)
,
f
m
(
x
(
i
)
)
)
>
0
\begin{aligned}&L(y^{(i)},f_m(x^{(i)}))<L(y^{(i)},f_{m-1}(x^{(i)}))\rightarrow L(y^{(i)},f_{m-1}(x^{(i)}))-L(y^{(i)},f_m(x^{(i)}))>0\end{aligned}
L(y(i),fm(x(i)))<L(y(i),fm−1(x(i)))→L(y(i),fm−1(x(i)))−L(y(i),fm(x(i)))>0
2.梯度提升
1.计算当前损失函数的负梯度表达式
L ( y , f m ( x ) ) = log ( 1 + e − f m ( x ) ) + ( 1 − y ) ⋅ f m ( x ) L(y,f_m(x))=\log(1+e^{-f_m(x)})+(1-y)\cdot f_m(x) L(y,fm(x))=log(1+e−fm(x))+(1−y)⋅fm(x)
∂ L ( y , f m ( x ) ) ∂ f m ( x ) = ∂ [ log ( 1 + e − f m ( x ) ) + ( 1 − y ) ⋅ f m ( x ) ] ∂ f m ( x ) = ∂ log ( 1 + e − f m ( x ) ) ∂ f m ( x ) + ∂ ( 1 − y ) ⋅ f m ( x ) ∂ f m ( x ) = − e − f m ( x ) 1 + e − f m ( x ) + 1 − y = − e − f m ( x ) + ( 1 − y ) ( 1 + e − f m ( x ) ) 1 + e − f m ( x ) = 1 − ( 1 + e − f m ( x ) ) y 1 + e − f m ( x ) = 1 1 + e − f m ( x ) − y \begin{aligned}\frac{\partial L(y,f_m(x))}{\partial f_m(x)}&=\frac{\partial \left[\log(1+e^{-f_m(x)})+(1-y)\cdot f_m(x)\right]}{\partial f_m(x)}\\&=\frac{\partial \log(1+e^{-f_m(x)})}{\partial f_m(x)}+\frac{\partial(1-y)\cdot f_m(x)}{\partial f_m(x)}\\&=-\frac{e^{-f_m(x)}}{1+e^{-f_m(x)}}+1-y\\&=\frac{-e^{-f_m(x)}+(1-y)(1+e^{-f_m(x)})}{1+e^{-f_m(x)}}\\&=\frac{1-(1+e^{-f_m(x)})y}{1+e^{-f_m(x)}}\\&=\frac{1}{1+e^{-f_m(x)}}-y\end{aligned} ∂fm(x)∂L(y,fm(x))=∂fm(x)∂[log(1+e−fm(x))+(1−y)⋅fm(x)]=∂fm(x)∂log(1+e−fm(x))+∂fm(x)∂(1−y)⋅fm(x)=−1+e−fm(x)e−fm(x)+1−y=1+e−fm(x)−e−fm(x)+(1−y)(1+e−fm(x))=1+e−fm(x)1−(1+e−fm(x))y=1+e−fm(x)1−y
2.构造新的训练样本
将 ( x i , y i ) (x_i,y_i) (xi,yi)代入 r m ( x , y ) r_m(x,y) rm(x,y)即可得到 r m 1 r_{m1} rm1,进而得到第m轮的训练数据集:
T m = { ( x 1 , r m 1 ) , ( x 2 , r m 2 ) , ⋯ , ( x N , r m N ) } T_m=\{(x_1,r_{m1}),(x_2,r_{m2}),\cdots,(x_N,r_{mN})\} Tm={(x1,rm1),(x2,rm2),⋯,(xN,rmN)}
r m ( x , y ) = − [ ∂ L ( y , f m ( x ) ) ∂ f m ( x ) ] f m ( x ) = f m − 1 ( x ) = − [ 1 1 + e − f m − 1 ( x ) − y ] = y − y ^ m − 1 r_m(x,y)=-\left[\frac{\partial L(y,f_m(x))}{\partial f_m(x)}\right]_{f_m(x)=f_{m-1}(x)}=-\left[\frac{1}{1+e^{-f_{m-1}(x)}}-y\right]=y-\hat y_{m-1} rm(x,y)=−[∂fm(x)∂L(y,fm(x))]fm(x)=fm−1(x)=−[1+e−fm−1(x)1−y]=y−y^m−1
即: r m i = y i − y ^ m − 1 , i r_{mi}=y_i-\hat y_{m-1,i} rmi=yi−y^m−1,i。
3.让当前的回归树拟合上述训练样本,得到 T ( x ; Θ m ) T(x;\Theta_m) T(x;Θm)。
3.面临问题
1.如何构造回归树
T
(
x
;
Θ
m
)
T(x;\Theta_m)
T(x;Θm)
- 1.树的深度如何决定
- 2.划分节点如何选取
- 3.叶子节点代表的值 c m c_m cm如何定
2.如何衡量
T
(
x
;
Θ
m
)
T(x;\Theta_m)
T(x;Θm)对残差(负梯度)的拟合效果?
使用传统的损失函数无法达到最优效果,使用总体损失又缺乏闭式解。
划分方式
→
\rightarrow
→损失函数:
1
n
∑
i
=
1
n
(
f
(
x
i
)
−
r
m
i
)
\frac{1}{n}\sum_{i=1}^n(f(x_i)-r_{mi})
n1i=1∑n(f(xi)−rmi),
c
m
j
∗
=
1
N
m
j
∑
x
i
∈
R
m
j
r
m
i
c_{mj}^*=\frac{1}{N_{mj}}\sum_{x_i\in R_{mj}}r_{mi}
cmj∗=Nmj1xi∈Rmj∑rmi
划分方式 → \rightarrow → 负梯度拟合效果 ⇔ \Leftrightarrow ⇔损失函数:总体损失 ∑ x i ∈ R m j [ log ( 1 + e − f m ( x i ) ) + ( 1 − y i ) ⋅ f m ( x i ) ] \sum_{x_i\in R_{mj}}\left[\log(1+e^{-f_m(x_i)})+(1-y_i)\cdot f_m(x_i)\right] xi∈Rmj∑[log(1+e−fm(xi))+(1−yi)⋅fm(xi)], c m j ∗ = arg min ∑ x i ∈ R m j L ( y i , f m − 1 ( x i ) + c m j ) c_{mj}^*=\arg\min\sum_{x_i\in R_{mj}}L(y_i,f_{m-1}(x_i)+c_{mj}) cmj∗=argminxi∈Rmj∑L(yi,fm−1(xi)+cmj)
为了得到闭式解:
使用总体损失的大小来衡量负梯度的拟合效果,是最好的但是该优化无法得到闭式解。通过泰勒二阶展开,得到闭式解:
C m j ∗ = ∑ x i ∈ R m j r m i ∑ x i ∈ R m j ( y i − r m i ) ( 1 − y i + r m i ) C_{mj}^*=\frac{\sum_{x_i\in R_{mj}}r_{mi}}{\sum_{x_i\in R_{mj}}(y_i-r_{mi})(1-y_i+r_{mi})} Cmj∗=∑xi∈Rmj(yi−rmi)(1−yi+rmi)∑xi∈Rmjrmi
推导过程:
二阶泰勒展开:
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 1 2 f " ( x 0 ) ( x − x 0 ) 2 f(x)\approx f(x_0)+f^{'}(x_0)(x-x_0)+\frac{1}{2}f^{"}(x_0)(x-x_0)^2 f(x)≈f(x0)+f′(x0)(x−x0)+21f"(x0)(x−x0)2
对 L ( y i , f m − 1 ( x i ) + C m j ) L(y_i,f_{m-1}(x_i)+C_{mj}) L(yi,fm−1(xi)+Cmj)进行二阶泰勒展开,其中 x i ∈ R m j x_i\in R_{mj} xi∈Rmj
L ( y i , f m − 1 ( x i ) + C m j ) ≈ L ( y i , f m − 1 ( x i ) ) + ∂ L ( y i , f m ( x i ) ) ∂ f m ( x i ) ∣ f m ( x i ) = f m − 1 ( x i ) ⋅ C m j + ∂ 2 L ( y i , f m ( x i ) ) ∂ f m ( x i ) 2 ∣ f m ( x i ) = f m − 1 ( x i ) ⋅ C m j 2 = L ( y , f m − 1 ( x ) ) − + ( y ^ m − 1 , i − y i ) C m j + 1 2 y ^ m − 1 , i ( 1 − y ^ m − 1 , i ) C m j 2 , 其中 x i ∈ R m j \begin{aligned}L(y_i,f_{m-1}(x_i)+C_{mj})&\approx L(y_i,f_{m-1}(x_i))+\frac{\partial L(y_i,f_m(x_i))}{\partial f_m(x_i)}|_{f_m(x_i)=f_{m-1}(x_i)}\cdot C_{mj}+\frac{\partial^2 L(y_i,f_m(x_i))}{\partial f_m(x_i)^2}|_{f_m(x_i)=f_{m-1}(x_i)}\cdot C_{mj}^2\\& = L(y,f_{m-1}(x))-+(\hat y_{m-1,i}-y_i)C_{mj}+\frac{1}{2}\hat y_{m-1,i}(1-\hat y_{m-1,i})C_{mj}^2,其中x_i \in R_{mj}\end{aligned} L(yi,fm−1(xi)+Cmj)≈L(yi,fm−1(xi))+∂fm(xi)∂L(yi,fm(xi))∣fm(xi)=fm−1(xi)⋅Cmj+∂fm(xi)2∂2L(yi,fm(xi))∣fm(xi)=fm−1(xi)⋅Cmj2=L(y,fm−1(x))−+(y^m−1,i−yi)Cmj+21y^m−1,i(1−y^m−1,i)Cmj2,其中xi∈Rmj
因此有:
C m j ∗ = arg min ∑ x i ∈ R m j L ( y i , f m − 1 ( x i ) + C m j ) C_{mj}^*=\arg\min\sum_{x_i\in R_{mj}}L(y_i,f_{m-1}(x_i)+C_{mj}) Cmj∗=argminxi∈Rmj∑L(yi,fm−1(xi)+Cmj)
∑ x i ∈ R m j L ( y i , f m − 1 ( x i ) + C m j ) = ∑ x i ∈ R m j [ L ( y , f m − 1 ( x ) ) + ( y ^ m − 1 , i − y i ) C m j + 1 2 y ^ m − 1 , i ( 1 − y ^ m − 1 , i ) C m j 2 ] , 其中 x i ∈ R m j = ∑ x i ∈ R m j L ( y , f m − 1 ( x ) ) + N m j C m j ∑ x i ∈ R m j ( y ^ m − 1 , i − y i ) + 1 2 N m j C m j 2 ∑ x i ∈ R m j ( 1 − y ^ m − 1 , i ) y ^ m − 1 , i \begin{aligned}\sum_{x_i\in R_{mj}}L(y_i,f_{m-1}(x_i)+C_{mj})&=\sum_{x_i\in R_{mj}}\left[L(y,f_{m-1}(x))+(\hat y_{m-1,i}-y_i)C_{mj}+\frac{1}{2}\hat y_{m-1,i}(1-\hat y_{m-1,i})C_{mj}^2\right],其中x_i \in R_{mj}\\&=\sum_{x_i\in R_{mj}}L(y,f_{m-1}(x))+N_{mj}C_{mj}\sum_{x_i\in R_{mj}}(\hat y_{m-1,i}-y_i)+\frac{1}{2}N_{mj}C_{mj}^2\sum_{x_i\in R_{mj}}(1-\hat y_{m-1,i})\hat y_{m-1,i}\end{aligned} xi∈Rmj∑L(yi,fm−1(xi)+Cmj)=xi∈Rmj∑[L(y,fm−1(x))+(y^m−1,i−yi)Cmj+21y^m−1,i(1−y^m−1,i)Cmj2],其中xi∈Rmj=xi∈Rmj∑L(y,fm−1(x))+NmjCmjxi∈Rmj∑(y^m−1,i−yi)+21NmjCmj2xi∈Rmj∑(1−y^m−1,i)y^m−1,i
式中只有 C m j C_{mj} Cmj为变量,且是一个一元二次方程, ( 1 − y ^ m − 1 , i ) y ^ m − 1 , i > 0 (1-\hat y_{m-1,i})\hat y_{m-1,i}>0 (1−y^m−1,i)y^m−1,i>0,开口向上,有最小值当且仅当:
C m j ∗ = − b 2 a = − N m j ⋅ ∑ x i ∈ R m j ( y ^ m − 1 , i − y i ) N m j ⋅ ∑ x i ∈ R m j ( 1 − y ^ m − 1 , i ) y ^ m − 1 , i = − ∑ x i ∈ R m j ( y ^ m − 1 , i − y i ) ∑ x i ∈ R m j ( 1 − y ^ m − 1 , i ) y ^ m − 1 , i , 因为 r m i = y i − y ^ m − 1 , i = ∑ x i ∈ R m j r m i ∑ x i ∈ R m j ( y i − r m i ) ( 1 − y i + r m i ) \begin{aligned}C_{mj}^*&=-\frac{b}{2a}=-\frac{N_{mj}\cdot\sum_{x_i\in R_{mj}}(\hat y_{m-1,i}-y_i)}{N_{mj}\cdot\sum_{x_i\in R_{mj}}(1-\hat y_{m-1,i})\hat y_{m-1,i}}\\&=-\frac{\sum_{x_i\in R_{mj}}(\hat y_{m-1,i}-y_i)}{\sum_{x_i\in R_{mj}}(1-\hat y_{m-1,i})\hat y_{m-1,i}},因为r_{mi}=y_i-\hat y_{m-1,i}\\&=\frac{\sum_{x_i\in R_{mj}} r_{mi}}{\sum_{x_i\in R_{mj}}(y_i-r_{mi})(1-y_i+r_{mi})}\end{aligned} Cmj∗=−2ab=−Nmj⋅∑xi∈Rmj(1−y^m−1,i)y^m−1,iNmj⋅∑xi∈Rmj(y^m−1,i−yi)=−∑xi∈Rmj(1−y^m−1,i)y^m−1,i∑xi∈Rmj(y^m−1,i−yi),因为rmi=yi−y^m−1,i=∑xi∈Rmj(yi−rmi)(1−yi+rmi)∑xi∈Rmjrmi
4.结论
通过不同的划分方式得到多棵树,然后计算总体损失,最后选择损失最小的那颗树。
- 1.使用总体损失对回归树进行优化,计算过于复杂。
- 2.两种方法得出的划分方式(即树的结构)是一样的。
于是: - 1.使用传统回归树构建好回归树的结构(就是用MSE计算损失)。
- 2.再使用总体损失中的方式计算树的叶子节点中的 c m j c_{mj} cmj。






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








