函数曲线长度的计算方法

最新推荐文章于 2023-01-18 11:09:55 发布

麦克斯韦的妖精

最新推荐文章于 2023-01-18 11:09:55 发布

阅读量2w

点赞数 5

分类专栏：随笔文章标签：函数曲线长度定积分数学

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/john_bian/article/details/103067564

版权

随笔专栏收录该内容

14 篇文章

订阅专栏

有些情况下，我们需要知道曲线上两个点之间在曲线上的测地距离。例如，在下图的二次函数曲线中，我们想知道从点（2，4）沿着曲线到点（8,64）要走的路程。

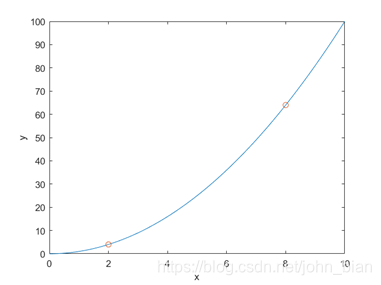
对此，我们可以将对应的函数区间划分为多个小的区间，每个小区间上两个端点之间的函数曲线长度可以用两个端点之间欧氏距离来代替，我们要求的图中两个点之间的曲线长度，就可以近似为划分的小区间端点之间欧氏距离之和。而当我们划分的小区间有无穷多个的时候，二者相等。所以，这个问题可以用定积分来进行求解。

如下图所示，图中蓝色曲线是函数曲线，红色线段是用来近似函数曲线的线段。

则红色线段的长度 $\hat{L}$ 可以近似为

$\hat{L}=\sqrt{(dx)^2+(dy)^2}=\sqrt{(dx)^2+(dx\cdot f'(x))^2}=\sqrt{1+(f'(x))^2}\cdot dx$

所以曲线的长度可以表示为

$L=\int_{a}^{b}\sqrt{1+(f'(x))^2}dx$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。