1 HMM 前向后向算法推导
1.1 HMM基础知识点
对于HMM模型,其主要是处理序列问题,并且该问题包括一个表象的观测序列和一个可能无法直接观察到的隐藏序列(或者叫状态序列),且这两个序列都是包括
T
T
T个时刻的序列。观测序列的数学表达如式(1),状态序列的数学表达如式(2):
O
=
{
o
1
,
o
2
,
.
.
.
,
o
T
}
O=\lbrace o_1,o_2,...,o_T \rbrace
O={o1,o2,...,oT}
Q = { q 1 , q 2 , . . . , q T } Q=\lbrace q_1,q_2,...,q_T \rbrace Q={q1,q2,...,qT}
对于观测序列的每一个
o
t
o_t
ot可以有
N
N
N个不同的观测值,对于状态序列的每一个
q
t
q_t
qt可以有
M
M
M个不同的状态值,具体的数学表达如下:
o
t
=
{
v
1
,
v
2
,
.
.
.
,
v
N
}
o_t=\lbrace v_1,v_2,...,v_N\rbrace
ot={v1,v2,...,vN}
q t = { σ 1 , σ 2 , . . . , σ M } q_t=\lbrace \sigma_1,\sigma_2,...,\sigma_M\rbrace qt={σ1,σ2,...,σM}
HMM中有两个重要的假设:
- 齐次马尔科夫链假设。也就是说任意时刻的隐藏状态都只和前一时刻的隐藏状态有关,如式(5)。因此产生了一个概念,就是隐状态转移概率, a i j a_{ij} aij,表示隐藏状态从 t t t时刻的状态 i i i转换为 t + 1 t+1 t+1时刻的状态 j j j的概率。每一个隐状态转移到另一个状态的概率集合可以通过状态转移矩阵来表示,如(5)(6)。
P ( q t + 1 ∣ q t , q t − 1 , q t − 2 , . . . , q 1 ) = P ( q t + 1 ∣ q t ) P(q_{t+1}|q_t,q_{t-1},q_{t-2},...,q_{1})=P(q_t+1|q_t) P(qt+1∣qt,qt−1,qt−2,...,q1)=P(qt+1∣qt)
A = [ a i j ] M × M ; i ∈ { 1 , 2 , . . . , M } , j ∈ { 1 , 2 , . . . , M } A=[a_{ij}]_{M\times M} ;i\in\{1,2,...,M\},j\in\{1,2,...,M\} A=[aij]M×M;i∈{1,2,...,M},j∈{1,2,...,M}
- 观测独立性假设。也就是说任意时刻的观测状态只与当前时刻的隐藏状态有关,如式(7)。因此产生了一个概念,就是发射概率 b j ( k ) b_j(k) bj(k),表示在时刻 t t t时隐藏状态 q t q_t qt是 i j i_j ij时,观测结果 o t o_t ot是 v k v_k vk的概率。每一个有状态到每一个不同的观测结果的发射概率的集合可以通过发射矩阵来表示,如(8)。
P ( o t ∣ q t , q t − 1 , . . . , q 1 ) = P ( o t ∣ q t ) P(o_t|q_t,q_{t-1},...,q_1)=P(o_t|q_t) P(ot∣qt,qt−1,...,q1)=P(ot∣qt)
B = [ b j ( k ) ] M × N ; j ∈ { 1 , 2 , . . . , M } , k ∈ { 1 , 2 , . . . , N } B=[b_j(k)]_{M\times N};j\in\{1,2,...,M\},k\in\{1,2,...,N\} B=[bj(k)]M×N;j∈{1,2,...,M},k∈{1,2,...,N}
除了上面的隐状态转移矩阵和发射矩阵,还需要一个在
t
=
1
t=1
t=1时每一个隐藏状态的初始分布
Π
\Pi
Π,如(9)所示。
Π
=
[
π
(
i
)
]
N
;
π
(
i
)
=
P
(
q
1
=
i
)
;
i
∈
{
1
,
2
,
.
.
.
,
M
}
\Pi=[\pi(i)]_N;\pi(i)=P(q_1=i);i\in\{1,2,...,M\}
Π=[π(i)]N;π(i)=P(q1=i);i∈{1,2,...,M}
因此,一个HMM模型可以通过一个三元组
λ
(
A
,
B
,
Π
)
\lambda(A,B,\Pi)
λ(A,B,Π)来表示。
1.2 前向后向算法
前向和后向算法都是为了解决HMM中的第一个问题,即在观测序列 O O O和模型参数 λ \lambda λ都已知,状态序列 Q Q Q未知的条件下求产生这样的观测序列的概率是多少,也就是求 P ( O ∣ λ ) = ∑ Q P ( O , Q ∣ λ ) P(O|\lambda)=\sum_QP(O,Q|\lambda) P(O∣λ)=∑QP(O,Q∣λ)。由于通过暴力搜索来计算每一种隐状态序列产生观测序列概率的复杂度很高, Θ ( T N T ) \Theta(TN^T) Θ(TNT),所以需要通过前向后向算法来简化计算的复杂度, Θ ( T N 2 ) \Theta(TN^2) Θ(TN2)。
1.2.1 前向算法
前向算法的推导可以通过动态规划的思想逐步求解出来,首先我们定义前向概率,即观测序列是
o
1
,
o
2
,
.
.
.
,
o
t
o_1,o_2,...,o_t
o1,o2,...,ot,且
t
t
t时刻的隐状态是
σ
i
\sigma_i
σi时的概率,数学表达如式(10):
α
t
(
i
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
i
∣
λ
)
;
i
∈
{
1
,
2
,
.
.
.
,
M
}
\alpha_t(i)=P(o_1,o_2,...,o_t,q_t=\sigma_i|\lambda);i\in\{1,2,...,M\}
αt(i)=P(o1,o2,...,ot,qt=σi∣λ);i∈{1,2,...,M}
前向算法推导过程如下所示:
α
t
+
1
(
i
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
o
t
+
1
,
q
t
+
1
=
σ
j
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
o
t
+
1
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
o
t
+
1
∣
q
t
+
1
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
+
1
=
σ
j
∣
λ
)
P
(
o
t
+
1
∣
q
t
+
1
,
λ
)
=
∑
i
M
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
i
,
q
t
+
1
=
σ
j
∣
λ
)
P
(
o
t
+
1
∣
q
t
+
1
,
λ
)
=
∑
i
M
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
P
(
q
t
=
σ
i
∣
λ
)
P
(
o
t
+
1
∣
q
t
+
1
,
λ
)
=
∑
i
M
P
(
o
1
,
o
2
,
.
.
.
,
o
t
∣
q
t
=
σ
i
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
P
(
q
t
=
σ
i
∣
λ
)
P
(
o
t
+
1
∣
q
t
+
1
,
λ
)
=
∑
i
M
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
i
∣
λ
)
P
(
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
P
(
o
t
+
1
∣
q
t
+
1
,
λ
)
=
[
∑
i
M
α
t
(
i
)
a
i
j
]
b
j
(
o
t
+
1
)
=
[
∑
i
M
α
t
(
i
)
×
状态转移概率
]
×
发射概率
\begin{aligned} \alpha_{t+1}(i) & =P(o_1,o_2,...,o_t,o_{t+1},q_{t+1}=\sigma_j|\lambda) \\ & = P(o_1,o_2,...,o_t,o_{t+1}|q_{t+1}=\sigma_j,\lambda)P(q_{t+1}=\sigma_j|\lambda)\\ & = P(o_1,o_2,...,o_t|q_{t+1}=\sigma_j,\lambda)P(o_{t+1}|q_{t+1},\lambda)P(q_{t+1}=\sigma_j|\lambda)\\ & = P(o_1,o_2,...,o_t,q_{t+1}=\sigma_j|\lambda)P(o_{t+1}|q_{t+1},\lambda)\\ & =\sum_{i}^MP(o_1,o_2,...,o_t,q_t=\sigma_i,q_{t+1}=\sigma_j|\lambda)P(o_{t+1}|q_{t+1},\lambda) \\ & =\sum_{i}^MP(o_1,o_2,...,o_t,q_{t+1}=\sigma_j|q_t=\sigma_i,\lambda)P(q_t=\sigma_i|\lambda)P(o_{t+1}|q_{t+1},\lambda) \\ & =\sum_{i}^MP(o_1,o_2,...,o_t|q_t=\sigma_i,\lambda)P(q_{t+1}=\sigma_j|q_t=\sigma_i,\lambda)P(q_t=\sigma_i|\lambda)P(o_{t+1}|q_{t+1},\lambda) \\ & =\sum_{i}^MP(o_1,o_2,...,o_t,q_t=\sigma_i|\lambda)P(q_{t+1}=\sigma_j|q_t=\sigma_i,\lambda)P(o_{t+1}|q_{t+1},\lambda) \\ & =\left[\sum_i^M\alpha_t(i)a_{ij}\right]b_j(o_{t+1}) \\ & =\left[\sum_i^M\alpha_t(i)\times状态转移概率\right]\times发射概率 \end{aligned}
αt+1(i)=P(o1,o2,...,ot,ot+1,qt+1=σj∣λ)=P(o1,o2,...,ot,ot+1∣qt+1=σj,λ)P(qt+1=σj∣λ)=P(o1,o2,...,ot∣qt+1=σj,λ)P(ot+1∣qt+1,λ)P(qt+1=σj∣λ)=P(o1,o2,...,ot,qt+1=σj∣λ)P(ot+1∣qt+1,λ)=i∑MP(o1,o2,...,ot,qt=σi,qt+1=σj∣λ)P(ot+1∣qt+1,λ)=i∑MP(o1,o2,...,ot,qt+1=σj∣qt=σi,λ)P(qt=σi∣λ)P(ot+1∣qt+1,λ)=i∑MP(o1,o2,...,ot∣qt=σi,λ)P(qt+1=σj∣qt=σi,λ)P(qt=σi∣λ)P(ot+1∣qt+1,λ)=i∑MP(o1,o2,...,ot,qt=σi∣λ)P(qt+1=σj∣qt=σi,λ)P(ot+1∣qt+1,λ)=[i∑Mαt(i)aij]bj(ot+1)=[i∑Mαt(i)×状态转移概率]×发射概率
因此,问题一的最终结果是
P
(
O
∣
λ
)
=
∑
i
M
α
T
(
i
)
P(O|\lambda)=\sum_i^M\alpha_T(i)
P(O∣λ)=∑iMαT(i),其中
α
T
(
i
)
\alpha_T(i)
αT(i)可以通过以上的公式推导逐步的计算出来。
1.2.2 后向算法
后向算法的推导和前向算法的思想一样,都是通过动态规划的思想逐步推导出最终结果。和前向概率一样,我们需要先定义一个后向概率如式(12)。
β
t
+
1
(
j
)
=
P
(
o
t
+
2
,
o
t
+
3
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
λ
)
\beta_{t+1}(j)=P(o_{t+2},o_{t+3},...,o_T|q_{t+1}=\sigma_j,\lambda)
βt+1(j)=P(ot+2,ot+3,...,oT∣qt+1=σj,λ)
后向算法推导过程如下所示:
β
t
(
i
)
=
P
(
o
t
+
1
,
o
t
+
2
,
.
.
.
,
o
T
∣
q
t
=
σ
i
,
λ
)
=
∑
j
M
P
(
o
t
+
1
,
o
t
+
2
,
.
.
.
,
o
T
,
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
=
∑
j
M
P
(
o
t
+
1
,
o
t
+
2
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
q
t
=
σ
i
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
=
∑
j
M
P
(
o
t
+
1
,
o
t
+
2
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
=
∑
j
M
P
(
o
t
+
2
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
P
(
o
t
+
1
∣
q
t
+
1
=
σ
j
,
λ
)
=
∑
j
M
β
t
+
1
(
j
)
a
i
j
b
j
(
o
t
+
1
)
=
∑
j
M
β
t
+
1
(
j
)
×
状态转移概率
×
发射概率
\begin{aligned} \beta_t(i) &= P(o_{t+1},o_{t+2},...,o_T|q_{t}=\sigma_i,\lambda) \\ & =\sum_{j}^MP(o_{t+1},o_{t+2},...,o_T,q_{t+1}=\sigma_j|q_{t}=\sigma_i,\lambda) \\ & =\sum_j^MP(o_{t+1},o_{t+2},...,o_T|q_{t+1}=\sigma_j,q_{t}=\sigma_i,\lambda)P(q_{t+1}=\sigma_j|q_{t}=\sigma_i,\lambda) \\ & =\sum_j^MP(o_{t+1},o_{t+2},...,o_T|q_{t+1}=\sigma_j,\lambda)P(q_{t+1}=\sigma_j|q_{t}=\sigma_i,\lambda) \\ & =\sum_j^MP(o_{t+2},...,o_T|q_{t+1}=\sigma_j,\lambda)P(q_{t+1}=\sigma_j|q_{t}=\sigma_i,\lambda)P(o_{t+1}|q_{t+1}=\sigma_j,\lambda) \\ & =\sum_j^M\beta_{t+1}(j)a_{ij}b_j(o_{t+1}) \\ & =\sum_j^M\beta_{t+1}(j)\times状态转移概率\times发射概率 \end{aligned}
βt(i)=P(ot+1,ot+2,...,oT∣qt=σi,λ)=j∑MP(ot+1,ot+2,...,oT,qt+1=σj∣qt=σi,λ)=j∑MP(ot+1,ot+2,...,oT∣qt+1=σj,qt=σi,λ)P(qt+1=σj∣qt=σi,λ)=j∑MP(ot+1,ot+2,...,oT∣qt+1=σj,λ)P(qt+1=σj∣qt=σi,λ)=j∑MP(ot+2,...,oT∣qt+1=σj,λ)P(qt+1=σj∣qt=σi,λ)P(ot+1∣qt+1=σj,λ)=j∑Mβt+1(j)aijbj(ot+1)=j∑Mβt+1(j)×状态转移概率×发射概率
因此,问题一的最终结果是
P
(
O
∣
λ
)
=
∑
i
π
(
i
)
b
i
(
o
1
)
β
1
(
i
)
P(O|\lambda)=\sum_i\pi(i)b_i(o_1)\beta_1(i)
P(O∣λ)=∑iπ(i)bi(o1)β1(i),其中
β
1
(
i
)
\beta_1(i)
β1(i)可以通过以上的公式推导逐步的计算出来。
1.2.3 衍生公式推导
根据前向和后向算法我们可以推导出其他的公式。如式(14)所示,是在模型参数
λ
\lambda
λ和观测序列
O
O
O都已知的情况下,
t
t
t时刻的隐状态是
σ
i
\sigma_i
σi的概率。
γ
t
(
i
)
=
P
(
q
t
=
σ
i
∣
O
,
λ
)
=
P
(
O
,
q
t
=
σ
i
∣
λ
)
P
(
O
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
i
∣
λ
)
∑
j
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
j
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
T
∣
q
t
=
σ
i
,
λ
)
P
(
q
t
=
σ
i
∣
λ
)
∑
j
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
∣
q
t
=
σ
j
,
λ
)
P
(
q
t
=
σ
j
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
i
∣
λ
)
P
(
o
t
+
1
,
o
t
+
2
,
.
.
.
,
o
T
∣
q
t
=
σ
i
,
λ
)
∑
j
M
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
j
∣
λ
)
P
(
o
t
+
1
,
o
t
+
2
,
.
.
.
,
o
T
∣
q
t
=
σ
j
,
λ
)
=
α
t
(
i
)
β
t
(
i
)
∑
j
M
α
t
(
j
)
β
t
(
j
)
\begin{aligned} \gamma_t(i) & =P(q_t=\sigma_i|O,\lambda) \\ & =\frac{P(O,q_t=\sigma_i|\lambda)}{P(O|\lambda)} \\ & = \frac{P(o_1,o_2,...,o_T,q_t=\sigma_i|\lambda)}{\sum_j^MP(o_1,o_2,...,o_T,q_t=\sigma_j|\lambda)} \\ & =\frac{P(o_1,o_2,...,o_T|q_t=\sigma_i,\lambda)P(q_t=\sigma_i|\lambda)}{\sum_j^MP(o_1,o_2,...,o_T|q_t=\sigma_j,\lambda)P(q_t=\sigma_j|\lambda)} \\ & =\frac{P(o_1,o_2,...,o_t,q_t=\sigma_i|\lambda)P(o_{t+1},o_{t+2},...,o_T|q_t=\sigma_i,\lambda)}{\sum_j^MP(o_1,o_2,...,o_t,q_t=\sigma_j|\lambda)P(o_{t+1},o_{t+2},...,o_T|q_t=\sigma_j,\lambda)} \\ & =\frac{\alpha_t(i)\beta_t(i)}{\sum_j^M\alpha_t(j)\beta_t(j)} \end{aligned}
γt(i)=P(qt=σi∣O,λ)=P(O∣λ)P(O,qt=σi∣λ)=∑jMP(o1,o2,...,oT,qt=σj∣λ)P(o1,o2,...,oT,qt=σi∣λ)=∑jMP(o1,o2,...,oT∣qt=σj,λ)P(qt=σj∣λ)P(o1,o2,...,oT∣qt=σi,λ)P(qt=σi∣λ)=∑jMP(o1,o2,...,ot,qt=σj∣λ)P(ot+1,ot+2,...,oT∣qt=σj,λ)P(o1,o2,...,ot,qt=σi∣λ)P(ot+1,ot+2,...,oT∣qt=σi,λ)=∑jMαt(j)βt(j)αt(i)βt(i)
如式(15)所示,在模型参数
λ
\lambda
λ和观测序列
O
O
O都已知的情况下,
t
t
t时刻的隐状态是
σ
i
\sigma_i
σi,
t
+
1
t+1
t+1时刻的隐状态是
σ
j
\sigma_j
σj的概率。
ξ
t
(
i
,
j
)
=
P
(
q
t
=
σ
i
,
q
t
+
1
=
σ
j
∣
O
,
λ
)
=
P
(
q
t
=
σ
i
,
q
t
+
1
=
σ
j
,
O
∣
λ
)
P
(
O
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
i
,
q
t
+
1
=
σ
j
∣
λ
)
∑
s
M
∑
r
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
s
,
q
t
+
1
=
σ
r
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
i
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
λ
)
∑
s
M
∑
r
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
s
,
q
t
+
1
=
σ
r
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
i
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
o
t
+
1
,
o
t
+
2
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
q
t
+
1
=
σ
j
∣
λ
)
∑
s
M
∑
r
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
s
,
q
t
+
1
=
σ
r
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
i
,
q
t
+
1
=
σ
j
∣
λ
)
P
(
o
t
+
1
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
o
t
+
2
,
o
t
+
3
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
λ
)
∑
s
M
∑
r
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
s
,
q
t
+
1
=
σ
r
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
,
λ
)
P
(
q
t
=
σ
i
∣
λ
)
P
(
o
t
+
1
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
o
t
+
2
,
o
t
+
3
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
λ
)
∑
s
M
∑
r
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
s
,
q
t
+
1
=
σ
r
∣
λ
)
=
P
(
o
1
,
o
2
,
.
.
.
,
o
t
,
q
t
=
σ
i
∣
λ
)
P
(
q
t
+
1
=
σ
j
∣
q
t
=
σ
i
)
P
(
o
t
+
1
∣
q
t
+
1
=
σ
j
,
λ
)
P
(
o
t
+
2
,
o
t
+
3
,
.
.
.
,
o
T
∣
q
t
+
1
=
σ
j
,
λ
)
∑
s
M
∑
r
M
P
(
o
1
,
o
2
,
.
.
.
,
o
T
,
q
t
=
σ
s
,
q
t
+
1
=
σ
r
∣
λ
)
=
α
t
(
i
)
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
∑
s
M
∑
r
M
α
t
(
s
)
a
s
r
b
r
(
o
t
+
1
)
β
t
+
1
(
r
)
\begin{aligned} \xi_t(i,j) & =P(q_t=\sigma_i,q_{t+1}=\sigma_j|O,\lambda) \\ & =\frac{P(q_t=\sigma_i,q_{t+1}=\sigma_j,O|\lambda)}{P(O|\lambda)} \\[2ex] & =\frac{P(o_1,o_2,...,o_T,q_t=\sigma_i,q_{t+1}=\sigma_j|\lambda)}{\sum_s^M\sum_r^MP(o_1,o_2,...,o_T,q_t=\sigma_s,q_{t+1}=\sigma_r|\lambda)} \\[4ex] & =\frac{P(o_1,o_2,...,o_T,q_t=\sigma_i|q_{t+1}=\sigma_j,\lambda)P(q_{t+1}=\sigma_j|\lambda)}{\sum_s^M\sum_r^MP(o_1,o_2,...,o_T,q_t=\sigma_s,q_{t+1}=\sigma_r|\lambda)} \\[4ex] & =\frac{P(o_1,o_2,...,o_t,q_t=\sigma_i|q_{t+1}=\sigma_j,\lambda)P(o_{t+1},o_{t+2},...,o_T|q_{t+1}=\sigma_j,\lambda)P(q_{t+1}=\sigma_j|\lambda)}{\sum_s^M\sum_r^MP(o_1,o_2,...,o_T,q_t=\sigma_s,q_{t+1}=\sigma_r|\lambda)} \\[4ex] & =\frac{P(o_1,o_2,...,o_t,q_t=\sigma_i,q_{t+1}=\sigma_j|\lambda)P(o_{t+1}|q_{t+1}=\sigma_j,\lambda)P(o_{t+2},o_{t+3},...,o_T|q_{t+1}=\sigma_j,\lambda)}{\sum_s^M\sum_r^MP(o_1,o_2,...,o_T,q_t=\sigma_s,q_{t+1}=\sigma_r|\lambda)} \\[4ex] & =\frac{P(o_1,o_2,...,o_t,q_{t+1}=\sigma_j|q_t=\sigma_i,\lambda)P(q_t=\sigma_i|\lambda)P(o_{t+1}|q_{t+1}=\sigma_j,\lambda)P(o_{t+2},o_{t+3},...,o_T|q_{t+1}=\sigma_j,\lambda)}{\sum_s^M\sum_r^MP(o_1,o_2,...,o_T,q_t=\sigma_s,q_{t+1}=\sigma_r|\lambda)} \\[4ex] & =\frac{P(o_1,o_2,...,o_t,q_t=\sigma_i|\lambda)P(q_{t+1}=\sigma_j|q_t=\sigma_i)P(o_{t+1}|q_{t+1}=\sigma_j,\lambda)P(o_{t+2},o_{t+3},...,o_T|q_{t+1}=\sigma_j,\lambda)}{\sum_s^M\sum_r^MP(o_1,o_2,...,o_T,q_t=\sigma_s,q_{t+1}=\sigma_r|\lambda)} \\[4ex] & =\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_s^M\sum_r^M\alpha_t(s)a_{sr}b_r(o_{t+1})\beta_{t+1}(r)} \end{aligned}
ξt(i,j)=P(qt=σi,qt+1=σj∣O,λ)=P(O∣λ)P(qt=σi,qt+1=σj,O∣λ)=∑sM∑rMP(o1,o2,...,oT,qt=σs,qt+1=σr∣λ)P(o1,o2,...,oT,qt=σi,qt+1=σj∣λ)=∑sM∑rMP(o1,o2,...,oT,qt=σs,qt+1=σr∣λ)P(o1,o2,...,oT,qt=σi∣qt+1=σj,λ)P(qt+1=σj∣λ)=∑sM∑rMP(o1,o2,...,oT,qt=σs,qt+1=σr∣λ)P(o1,o2,...,ot,qt=σi∣qt+1=σj,λ)P(ot+1,ot+2,...,oT∣qt+1=σj,λ)P(qt+1=σj∣λ)=∑sM∑rMP(o1,o2,...,oT,qt=σs,qt+1=σr∣λ)P(o1,o2,...,ot,qt=σi,qt+1=σj∣λ)P(ot+1∣qt+1=σj,λ)P(ot+2,ot+3,...,oT∣qt+1=σj,λ)=∑sM∑rMP(o1,o2,...,oT,qt=σs,qt+1=σr∣λ)P(o1,o2,...,ot,qt+1=σj∣qt=σi,λ)P(qt=σi∣λ)P(ot+1∣qt+1=σj,λ)P(ot+2,ot+3,...,oT∣qt+1=σj,λ)=∑sM∑rMP(o1,o2,...,oT,qt=σs,qt+1=σr∣λ)P(o1,o2,...,ot,qt=σi∣λ)P(qt+1=σj∣qt=σi)P(ot+1∣qt+1=σj,λ)P(ot+2,ot+3,...,oT∣qt+1=σj,λ)=∑sM∑rMαt(s)asrbr(ot+1)βt+1(r)αt(i)aijbj(ot+1)βt+1(j)
2 HMM Baum-Welch算法
Baum-Welch算法是用来解决HMM的第二个问题的,即在已知观测序列 O O O,但不知道隐状态序列 Q Q Q和模型参数 λ \lambda λ时,如何去估计参数 λ \lambda λ。
2.1 EM算法介绍和推导
由于Baum-Welch算法的推导过程其实是通过EM算法的思想来进行的,所以在这之前我们需要先对EM算法(Expectation-Maximization algorithm)进行简单的推导与介绍。
EM算法最初是为了解决数据缺失情况下参数的估计问题,算法通过迭代的方式不断更新参数直到最终收敛。其中,迭代的过程可以分为E步和M步,这也就是为什么该算法叫做EM 算法的原因。
2.1.1 Jensen不等式
Jensen不等式的定义如下:
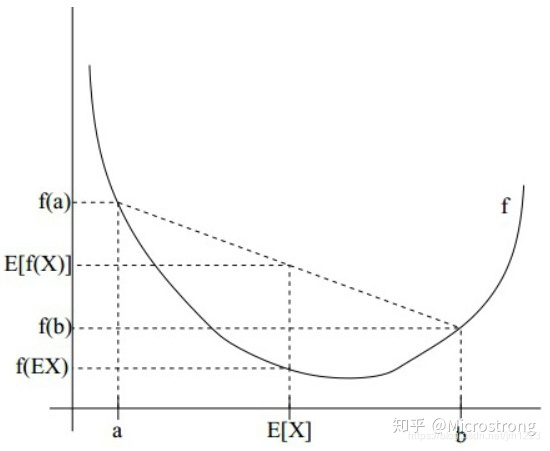
- 若函数 f ( x ) f(x) f(x)是凸函数, x x x是随机变量,那么 E ( f ( x ) ) ≥ f ( E ( x ) ) E(f(x))\ge f(E(x)) E(f(x))≥f(E(x))。当且仅当 x x x是常量时,不等式取等号成立。
- 若函数
f
(
x
)
f(x)
f(x)是凹函数,
x
x
x是随机变量,那么
E
(
f
(
x
)
)
≤
f
(
E
(
x
)
)
E(f(x))\le f(E(x))
E(f(x))≤f(E(x))。当且仅当
x
x
x是常量时,不等式取等号成立。
如下图所示,直观的对Jensen不等式进行理解。图片源于网络。
2.1.2 EM算法推导
假设样本集合
X
=
{
x
1
,
x
2
,
.
.
.
,
x
N
}
X=\{x_1,x_2,...,x_N\}
X={x1,x2,...,xN}包含
N
N
N个样本,模型需要估计的参数为
λ
\lambda
λ,模型的对数似然如式(16):
L
(
λ
)
=
∑
i
=
1
N
log
P
(
x
i
;
λ
)
L(\lambda)=\sum_{i=1}^N\log{P(x_i;\lambda)}
L(λ)=i=1∑NlogP(xi;λ)
而极大似然估计则是寻找一组能够使式(16)最大的模型参数作为最终的参数估计,即
λ
^
=
a
r
g
m
a
x
(
L
(
λ
)
)
\hat\lambda=argmax(L(\lambda))
λ^=argmax(L(λ))。
若我们得到的样本数据包含为观察到的隐藏数据
Z
=
{
z
1
,
z
2
,
.
.
.
,
z
N
}
Z=\{z_1,z_2,...,z_N\}
Z={z1,z2,...,zN},即每个样本对应的隐藏数据。此时我们最大化的对数似然将变为式(17)。
L
(
λ
)
=
∑
i
=
1
N
log
∑
z
i
P
(
x
i
,
z
i
;
λ
)
L(\lambda)=\sum_{i=1}^N\log\sum_{z_i}P(x_i,z_i;\lambda)
L(λ)=i=1∑Nlogzi∑P(xi,zi;λ)
接下来,假设隐藏数据服从某一分布
Q
(
z
i
)
Q(z_i)
Q(zi),对式(17)进行变换,如式(18)。
L
(
λ
)
=
∑
i
=
1
N
log
∑
z
i
P
(
x
i
,
z
i
;
λ
)
=
∑
i
=
1
N
log
∑
z
i
Q
(
z
i
)
P
(
x
i
,
z
i
;
λ
)
Q
(
z
i
)
≥
∑
i
=
1
N
∑
z
i
Q
(
z
i
)
log
P
(
x
i
,
z
i
;
λ
)
Q
(
z
i
)
\begin{aligned} L(\lambda) &=\sum_{i=1}^N\log\sum_{z_i}P(x_i,z_i;\lambda) \\ &=\sum_{i=1}^N\log\sum_{z_i}Q(z_i)\frac{P(x_i,z_i;\lambda)}{Q(z_i)} \\ &\ge \sum_{i=1}^N\sum_{z_i} Q(z_i)\log\frac{P(x_i,z_i;\lambda)}{Q(z_i)} \\ \end{aligned}
L(λ)=i=1∑Nlogzi∑P(xi,zi;λ)=i=1∑Nlogzi∑Q(zi)Q(zi)P(xi,zi;λ)≥i=1∑Nzi∑Q(zi)logQ(zi)P(xi,zi;λ)
式(1-3)中第二步到第三步是利用Jensen不等式完成的,由于
log
(
x
)
\log(x)
log(x)函数是一个凹函数,因此
E
(
f
(
x
)
)
≤
f
(
E
(
x
)
)
E(f(x))\le f(E(x))
E(f(x))≤f(E(x)),在这里是关于
Q
(
z
i
)
Q(z_i)
Q(zi)的期望。我们通过Jensen不等式确定了
L
(
λ
)
L(\lambda)
L(λ)的下界,在之前说过只有当函数内的随机变量取到常量时,Jensen不等式才会取到等号,也就是说
P
(
x
i
,
z
i
;
λ
)
Q
(
z
i
)
=
c
\frac{P(x_i,z_i;\lambda)}{Q(z_i)}=c
Q(zi)P(xi,zi;λ)=c,由于
∑
i
=
1
N
Q
(
z
i
)
=
1
\sum_{i=1}^NQ(z_i)=1
∑i=1NQ(zi)=1:
P
(
x
i
,
z
i
;
λ
)
Q
(
z
i
)
=
c
P
(
x
i
,
z
i
;
λ
)
=
c
Q
(
z
i
)
∑
z
i
P
(
x
i
,
z
i
;
λ
)
=
c
∑
z
i
Q
(
z
i
)
∑
z
i
N
P
(
x
i
,
z
i
;
λ
)
=
c
\frac{P(x_i,z_i;\lambda)}{Q(z_i)}=c\\ P(x_i,z_i;\lambda)=cQ(z_i) \\ \sum_{z_i}P(x_i,z_i;\lambda)=c\sum_{z_i}Q(z_i) \\ \sum_{z_i}^NP(x_i,z_i;\lambda)=c
Q(zi)P(xi,zi;λ)=cP(xi,zi;λ)=cQ(zi)zi∑P(xi,zi;λ)=czi∑Q(zi)zi∑NP(xi,zi;λ)=c
根据上式的推导,我们发现在Jensen不等式取等号时,
∑
z
i
P
(
x
i
,
z
i
;
λ
)
\sum_{z_i}P(x_i,z_i;\lambda)
∑ziP(xi,zi;λ)也取得常量,因此将常量用
∑
i
=
1
N
P
(
x
i
,
z
i
;
λ
)
\sum_{i=1}^NP(x_i,z_i;\lambda)
∑i=1NP(xi,zi;λ)替换后得(20):
P
(
x
i
,
z
i
;
λ
)
Q
(
z
i
)
=
∑
z
i
P
(
x
i
,
z
i
;
λ
)
\frac{P(x_i,z_i;\lambda)}{Q(z_i)}=\sum_{z_i}P(x_i,z_i;\lambda)
Q(zi)P(xi,zi;λ)=zi∑P(xi,zi;λ)
Q ( z i ) = P ( x i , z i ; λ ) ∑ z i P ( x i , z i ; λ ) = P ( x i , z i ; λ ) P ( x i ; λ ) = P ( z i ∣ x i ; λ ) Q(z_i)=\frac{P(x_i,z_i;\lambda)}{\sum_{z_i}P(x_i,z_i;\lambda)}=\frac{P(x_i,z_i;\lambda)}{P(x_i;\lambda)}=P(z_i|x_i;\lambda) Q(zi)=∑ziP(xi,zi;λ)P(xi,zi;λ)=P(xi;λ)P(xi,zi;λ)=P(zi∣xi;λ)
式(22)的推导展示了在Jensen不等式取得等号时
Q
(
z
i
)
Q(z_i)
Q(zi)实际上是后验概率,我们此时便可以确定
Q
(
z
i
)
Q(z_i)
Q(zi)的选择了,计算后验概率的这一步就是E步,在算法中利用上一次迭代得到的参数计算后验概率来对
Q
(
z
i
)
Q(z_i)
Q(zi)进行更新,下一步M步,我们固定计算好的
Q
(
z
i
)
=
P
(
z
i
∣
x
i
;
λ
^
)
Q(z_i)=P(z_i|x_i;\hat\lambda)
Q(zi)=P(zi∣xi;λ^)来最大化
∑
i
=
1
N
∑
z
i
Q
(
z
i
)
log
P
(
x
i
,
z
i
;
λ
)
Q
(
z
i
)
\sum_{i=1}^N\sum_{z_i} Q(z_i)\log\frac{P(x_i,z_i;\lambda)}{Q(z_i)}
∑i=1N∑ziQ(zi)logQ(zi)P(xi,zi;λ),即:
a
r
g
m
a
x
∑
i
=
1
N
∑
z
i
Q
(
z
i
)
log
P
(
x
i
,
z
i
;
λ
)
Q
(
z
i
)
=
a
r
g
m
a
x
∑
i
=
1
N
∑
z
i
P
(
z
i
∣
x
i
;
λ
^
)
log
P
(
x
i
,
z
i
;
λ
)
P
(
z
i
∣
x
i
;
λ
^
)
=
a
r
g
m
a
x
∑
i
=
1
N
∑
z
i
P
(
z
i
∣
x
i
;
λ
^
)
log
P
(
x
i
,
z
i
;
λ
)
−
∑
i
=
1
N
∑
z
i
P
(
z
i
∣
x
i
;
λ
^
)
log
P
(
z
i
∣
x
i
;
λ
^
)
=
a
r
g
m
a
x
∑
i
=
1
N
∑
z
i
P
(
z
i
∣
x
i
;
λ
^
)
log
P
(
x
i
,
z
i
;
λ
)
\begin{aligned} &argmax\sum_{i=1}^N\sum_{z_i} Q(z_i)\log\frac{P(x_i,z_i;\lambda)}{Q(z_i)} \\ &=argmax\sum_{i=1}^N\sum_{z_i} P(z_i|x_i;\hat\lambda)\log\frac{P(x_i,z_i;\lambda)}{P(z_i|x_i;\hat\lambda)} \\ &=argmax\sum_{i=1}^N\sum_{z_i} P(z_i|x_i;\hat\lambda)\log{P(x_i,z_i;\lambda)}-\sum_{i=1}^N\sum_{z_i}P(z_i|x_i;\hat\lambda)\log{P(z_i|x_i;\hat\lambda)} \\ &=argmax\sum_{i=1}^N\sum_{z_i} P(z_i|x_i;\hat\lambda)\log{P(x_i,z_i;\lambda)} \end{aligned}
argmaxi=1∑Nzi∑Q(zi)logQ(zi)P(xi,zi;λ)=argmaxi=1∑Nzi∑P(zi∣xi;λ^)logP(zi∣xi;λ^)P(xi,zi;λ)=argmaxi=1∑Nzi∑P(zi∣xi;λ^)logP(xi,zi;λ)−i=1∑Nzi∑P(zi∣xi;λ^)logP(zi∣xi;λ^)=argmaxi=1∑Nzi∑P(zi∣xi;λ^)logP(xi,zi;λ)
上式中第二步的第二项中由于是固定值所以不影响最终的结果,所以将其省略。因此,EM算法的M步就是寻找能够最大化上式
∑
i
=
1
N
∑
z
i
P
(
z
i
∣
x
i
;
λ
^
)
log
P
(
x
i
,
z
i
;
λ
)
\sum_{i=1}^N\sum_{z_i} P(z_i|x_i;\hat\lambda)\log{P(x_i,z_i;\lambda)}
∑i=1N∑ziP(zi∣xi;λ^)logP(xi,zi;λ)的模型参数
λ
\lambda
λ。
2.2 Baum-Welch算法推导
2.2.1 E步
由2.1节介绍,我们知道EM算法最后需要优化的是:
∑
i
=
1
N
∑
z
i
P
(
z
i
∣
x
i
;
λ
^
)
log
P
(
x
i
,
z
i
;
λ
)
\sum_{i=1}^N\sum_{z_i} P(z_i|x_i;\hat\lambda)\log{P(x_i,z_i;\lambda)}
i=1∑Nzi∑P(zi∣xi;λ^)logP(xi,zi;λ)
结合HMM算法中的观测序列和状态序列的定义,式(23)又可以写成式(24),其中K表示样本集合中序列样本的总数:
∑
k
=
1
K
∑
Q
P
(
Q
∣
O
k
,
λ
^
)
log
P
(
O
k
,
Q
;
λ
)
\sum_{k=1}^{K}\sum_{Q} P(Q|O_k,\hat\lambda)\log{P(O_k,Q;\lambda)}
k=1∑KQ∑P(Q∣Ok,λ^)logP(Ok,Q;λ)
假设我们的训练样本集是
{
O
1
,
O
2
,
.
.
.
,
O
K
}
\{O_1,O_2,...,O_K\}
{O1,O2,...,OK},对于其中的某一个
O
k
=
{
o
1
(
k
)
,
o
2
(
k
)
,
.
.
.
,
o
T
(
k
)
}
O_k=\{o_1^{(k)},o_2^{(k)},...,o_T^{(k)}\}
Ok={o1(k),o2(k),...,oT(k)},样本集对应的隐状态集是
{
Q
1
,
Q
2
,
.
.
.
,
Q
K
}
\{Q_1,Q_2,...,Q_K\}
{Q1,Q2,...,QK},对于其中的某一个
Q
k
=
{
q
1
(
k
)
,
q
2
(
k
)
,
.
.
.
,
q
T
(
k
)
}
Q_k=\{q_1^{(k)},q_2^{(k)},...,q_T^{(k)}\}
Qk={q1(k),q2(k),...,qT(k)}。对式(24)进一步分解为(25):
λ
^
:
=
a
r
g
m
a
x
λ
∑
k
=
1
K
∑
Q
P
(
O
k
,
Q
∣
λ
^
)
P
(
O
k
∣
λ
^
)
log
P
(
O
k
,
Q
∣
λ
)
\hat\lambda:=argmax_\lambda\sum_{k=1}^K\sum_Q\frac{P(O_k,Q|\hat\lambda)}{P(O_k|\hat\lambda)}\log{P(O_k,Q|\lambda)}
λ^:=argmaxλk=1∑KQ∑P(Ok∣λ^)P(Ok,Q∣λ^)logP(Ok,Q∣λ)
因为式(25)中由于
P
(
O
k
∣
λ
^
)
P(O_k|\hat\lambda)
P(Ok∣λ^)的值是固定的,因此可以忽略,式(25)则化简为式(26):
λ
^
:
=
a
r
g
m
a
x
λ
∑
k
=
1
K
∑
Q
P
(
O
k
,
Q
∣
λ
^
)
log
P
(
O
k
,
Q
∣
λ
)
\hat\lambda:=argmax_\lambda\sum_{k=1}^K\sum_QP(O_k,Q|\hat\lambda)\log{P(O_k,Q|\lambda)}
λ^:=argmaxλk=1∑KQ∑P(Ok,Q∣λ^)logP(Ok,Q∣λ)
式(26)就是我们最终需要优化的表达式,下面我们需要写出在模型参数为
λ
\lambda
λ时
O
O
O和
Q
Q
Q的联合概率分布的详细表达式,如式(27),其中式(26)中在
λ
^
\hat\lambda
λ^时
O
O
O和
Q
Q
Q的联合概率分布与式(27)一致,只是因为迭代次数的原因参数值不同而已。式(27)中
i
t
i^{t}
it表示序列
t
t
t时刻的隐状态为
i
i
i。
P
(
O
,
Q
∣
λ
)
=
π
(
i
(
1
)
)
b
i
(
1
)
(
o
1
)
a
i
(
1
)
i
(
2
)
b
i
(
2
)
(
o
2
)
.
.
.
a
i
(
T
−
1
)
i
(
T
)
b
i
(
T
)
(
o
T
)
P(O,Q|\lambda)=\pi(i^{(1)})b_{i^{(1)}}(o_1)a_{i^{(1)}i^{(2)}}b_{i^{(2)}}(o_2)...a_{i^{(T-1)}i^{(T)}}b_{i^{(T)}}(o_T)
P(O,Q∣λ)=π(i(1))bi(1)(o1)ai(1)i(2)bi(2)(o2)...ai(T−1)i(T)bi(T)(oT)
我们将式(27)进行重写整理,写成式(28)的样子,其中我们暂时忽略了样本集合中样本求和项:
λ
^
=
a
r
g
m
a
x
λ
∑
Q
P
(
O
,
Q
∣
λ
^
)
log
π
(
i
(
1
)
)
+
∑
Q
(
∑
t
=
1
T
−
1
log
a
i
(
t
)
i
(
t
+
1
)
)
P
(
O
,
Q
∣
λ
^
)
+
∑
Q
(
∑
t
=
1
T
b
i
(
t
)
(
o
t
)
)
P
(
O
,
Q
∣
λ
^
)
\begin{aligned} \hat\lambda =&argmax_\lambda\sum_QP(O,Q|\hat\lambda)\log\pi(i^{(1)})\\ &+\sum_Q\bigg(\sum_{t=1}^{T-1}\log{a_{i^{(t)}i^{(t+1)}}}\bigg)P(O,Q|\hat\lambda)+\sum_Q\bigg(\sum_{t=1}^{T}b_{i^{(t)}}(o_t)\bigg)P(O,Q|\hat\lambda) \end{aligned}
λ^=argmaxλQ∑P(O,Q∣λ^)logπ(i(1))+Q∑(t=1∑T−1logai(t)i(t+1))P(O,Q∣λ^)+Q∑(t=1∑Tbi(t)(ot))P(O,Q∣λ^)
2.2.2 M步
接下来的M步就是对式(28)中的三项分别去极大化,这里使用拉格朗日乘子法来解决有约束条件的情况下求取极值的问题,首先我们对第一项进行求解,我们将第一项写为式(29)所示,其中
∑
Q
P
(
O
,
Q
∣
λ
^
)
\sum_QP(O,Q|\hat\lambda)
∑QP(O,Q∣λ^)被改写为
∑
i
=
1
M
P
(
O
,
i
(
2
)
=
i
∣
λ
^
)
\sum_{i=1}^MP(O,i^{(2)}=i|\hat\lambda)
∑i=1MP(O,i(2)=i∣λ^)是因为在初始状态确定的条件下,我们只要遍历第二个时刻所有的隐状态就好,对于第三个时刻往后的概率计算因为HMM的齐次马尔可夫假设的原因,在不同的初始隐状态下的概率式是一样的,所以对原始第一项的极大化可以化简为式(29):
∑
Q
P
(
O
,
Q
∣
λ
^
)
log
π
(
i
(
1
)
)
=
∑
i
=
1
M
P
(
O
,
i
(
2
)
=
i
∣
λ
^
)
log
π
(
i
)
\sum_QP(O,Q|\hat\lambda)\log\pi(i^{(1)})=\sum_{i=1}^MP(O,i^{(2)}=i|\hat\lambda)\log\pi(i)
Q∑P(O,Q∣λ^)logπ(i(1))=i=1∑MP(O,i(2)=i∣λ^)logπ(i)
考虑到约束条件
∑
i
=
1
M
log
π
(
i
)
=
1
\sum_{i=1}^M\log\pi(i)=1
∑i=1Mlogπ(i)=1,利用拉格朗日乘子法,我们可以写出拉格朗日函数:
∑
i
=
1
M
P
(
O
,
i
(
2
)
=
i
∣
λ
^
)
log
π
(
i
)
+
γ
(
∑
i
=
1
M
π
(
i
)
−
1
)
\sum_{i=1}^MP(O,i^{(2)}=i|\hat\lambda)\log\pi(i)+\gamma\big(\sum_{i=1}^M\pi(i)-1\big)
i=1∑MP(O,i(2)=i∣λ^)logπ(i)+γ(i=1∑Mπ(i)−1)
对其求偏导并令结果为0:
∂
∂
π
(
i
)
[
∑
i
=
1
M
P
(
O
,
i
(
2
)
=
i
∣
λ
^
)
log
π
(
i
)
+
γ
(
∑
i
=
1
M
π
(
i
)
−
1
)
]
=
0
\frac{\partial}{\partial\pi(i)}\bigg[\sum_{i=1}^MP(O,i^{(2)}=i|\hat\lambda)\log\pi(i)+\gamma\big(\sum_{i=1}^M\pi(i)-1\big)\bigg]=0
∂π(i)∂[i=1∑MP(O,i(2)=i∣λ^)logπ(i)+γ(i=1∑Mπ(i)−1)]=0
求偏导并整理可得:
P
(
O
,
i
(
2
)
=
i
∣
λ
^
)
+
γ
π
(
i
)
=
0
P(O,i^{(2)}=i|\hat\lambda)+\gamma\pi(i)=0
P(O,i(2)=i∣λ^)+γπ(i)=0
对
i
i
i求和可得:
γ
=
−
P
(
O
∣
λ
^
)
\gamma=-P(O|\hat\lambda)
γ=−P(O∣λ^)
将式(35)带入到式(34)中可得:
π
(
i
)
=
P
(
O
,
i
(
2
)
=
i
∣
λ
^
)
P
(
O
∣
λ
^
)
\pi(i)=\frac{P(O,i^{(2)}=i|\hat\lambda)}{P(O|\hat\lambda)}
π(i)=P(O∣λ^)P(O,i(2)=i∣λ^)
式(28)中的第二项可以写为:
∑
Q
(
∑
t
=
1
T
−
1
log
a
i
(
t
)
i
(
t
+
1
)
)
P
(
O
,
Q
∣
λ
^
)
=
∑
i
=
1
M
∑
j
=
1
M
∑
t
=
1
T
−
1
log
a
i
j
P
(
O
,
i
(
t
)
=
i
,
i
(
t
+
1
)
=
j
∣
λ
^
)
\sum_Q\bigg(\sum_{t=1}^{T-1}\log{a_{i^{(t)}i^{(t+1)}}}\bigg)P(O,Q|\hat\lambda)=\sum_{i=1}^{M}\sum_{j=1}^{M}\sum_{t=1}^{T-1}\log{a_{ij}}P(O,i^{(t)}=i,i^{(t+1)}=j|\hat{\lambda})
Q∑(t=1∑T−1logai(t)i(t+1))P(O,Q∣λ^)=i=1∑Mj=1∑Mt=1∑T−1logaijP(O,i(t)=i,i(t+1)=j∣λ^)
考虑到约束条件
∑
j
=
1
M
a
i
j
=
1
\sum_{j=1}^{M}a_{ij}=1
∑j=1Maij=1,我们利用拉格朗日乘子法可得:
∑
i
=
1
M
∑
j
=
1
M
∑
t
=
1
T
−
1
log
a
i
j
P
(
O
,
i
(
t
)
=
i
,
i
(
t
+
1
)
=
j
∣
λ
^
)
+
γ
(
∑
j
=
1
M
a
i
j
−
1
)
\sum_{i=1}^{M}\sum_{j=1}^{M}\sum_{t=1}^{T-1}\log{a_{ij}}P(O,i^{(t)}=i,i^{(t+1)}=j|\hat{\lambda})+\gamma\big(\sum_{j=1}^{M}a_{ij}-1\big)
i=1∑Mj=1∑Mt=1∑T−1logaijP(O,i(t)=i,i(t+1)=j∣λ^)+γ(j=1∑Maij−1)
对上式中的
a
i
j
a_{ij}
aij求偏导:
P
(
O
,
i
(
t
)
=
i
,
i
(
t
+
1
)
=
j
∣
λ
^
)
+
a
i
j
γ
=
0
P(O,i^{(t)}=i,i^{(t+1)}=j|\hat{\lambda})+a_{ij}\gamma=0
P(O,i(t)=i,i(t+1)=j∣λ^)+aijγ=0
对
j
j
j求和可得:
γ
=
−
P
(
O
,
i
(
t
)
=
i
∣
λ
^
)
\gamma=-P(O,i^{(t)}=i|\hat{\lambda})
γ=−P(O,i(t)=i∣λ^)
将式(47)带入式(46)可得:
a
i
j
=
∑
t
=
1
T
−
1
P
(
O
,
i
(
t
)
=
i
,
i
(
t
+
1
)
=
j
∣
λ
^
)
∑
t
=
1
T
−
1
P
(
O
,
i
(
t
)
=
i
∣
λ
^
)
a_{ij}=\frac{\sum_{t=1}^{T-1}P(O,i^{(t)}=i,i^{(t+1)}=j|\hat{\lambda})}{\sum_{t=1}^{T-1}P(O,i^{(t)}=i|\hat{\lambda})}
aij=∑t=1T−1P(O,i(t)=i∣λ^)∑t=1T−1P(O,i(t)=i,i(t+1)=j∣λ^)
式(28)中的第三项可以写为:
∑
Q
(
∑
t
=
1
T
b
i
(
t
)
(
o
t
)
)
P
(
O
,
Q
∣
λ
^
)
=
∑
j
=
1
M
∑
t
=
1
T
log
b
j
(
o
t
)
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
\sum_Q\bigg(\sum_{t=1}^{T}b_{i^{(t)}}(o_t)\bigg)P(O,Q|\hat\lambda)=\sum_{j=1}^{M}\sum_{t=1}^T\log{b_j(o_t)}P(O,i^{(t)}=j|\hat\lambda)
Q∑(t=1∑Tbi(t)(ot))P(O,Q∣λ^)=j=1∑Mt=1∑Tlogbj(ot)P(O,i(t)=j∣λ^)
考虑到约束条件
∑
n
=
1
N
b
j
(
n
)
=
1
\sum_{n=1}^{N}b_j(n)=1
∑n=1Nbj(n)=1,只有在
o
t
=
v
n
o_t=v_n
ot=vn时
b
j
(
o
t
)
b_j({o_t})
bj(ot)对
b
j
(
n
)
b_j(n)
bj(n)的偏导才不为0,我们以示性函数
I
(
o
t
=
v
n
)
I(o_t=v_n)
I(ot=vn)表示。
∑
j
=
1
M
∑
t
=
1
T
log
b
j
(
o
t
)
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
+
λ
(
∑
n
=
1
M
b
j
(
n
)
−
1
)
\sum_{j=1}^{M}\sum_{t=1}^T\log{b_j(o_t)}P(O,i^{(t)}=j|\hat\lambda)+\lambda\big(\sum_{n=1}^{M}b_j(n)-1\big)
j=1∑Mt=1∑Tlogbj(ot)P(O,i(t)=j∣λ^)+λ(n=1∑Mbj(n)−1)
对上式中的
b
j
(
n
)
b_j(n)
bj(n)求偏导得:
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
I
(
o
t
=
v
n
)
+
λ
b
j
(
n
)
=
0
P(O,i^{(t)}=j|\hat\lambda)I(o_t=v_n)+\lambda{b_j(n)}=0
P(O,i(t)=j∣λ^)I(ot=vn)+λbj(n)=0
对
n
n
n求和可得:
λ
=
−
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
\lambda=-P(O,i^{(t)}=j|\hat\lambda)
λ=−P(O,i(t)=j∣λ^)
将上式带入式(64)中得:
b
j
(
n
)
=
∑
t
=
1
T
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
I
(
o
t
=
v
n
)
∑
t
=
1
T
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
b_j(n)=\frac{\sum_{t=1}^{T}P(O,i^{(t)}=j|\hat\lambda)I(o_t=v_n)}{\sum_{t=1}^{T}P(O,i^{(t)}=j|\hat\lambda)}
bj(n)=∑t=1TP(O,i(t)=j∣λ^)∑t=1TP(O,i(t)=j∣λ^)I(ot=vn)
2.3 公式的重写
从上一节中的推导中我们可以得到以下三个关键的结论性公式:
π
(
i
)
=
P
(
O
,
i
(
2
)
=
i
∣
λ
^
)
P
(
O
∣
λ
^
)
a
i
j
=
∑
t
=
1
T
−
1
P
(
O
,
i
(
t
)
=
i
,
i
(
t
+
1
)
=
j
∣
λ
^
)
∑
t
=
1
T
−
1
P
(
O
,
i
(
t
)
=
i
∣
λ
^
)
b
j
(
n
)
=
∑
t
=
1
T
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
I
(
o
t
=
v
n
)
∑
t
=
1
T
P
(
O
,
i
(
t
)
=
j
∣
λ
^
)
\pi(i)=\frac{P(O,i^{(2)}=i|\hat\lambda)}{P(O|\hat\lambda)} \\ a_{ij}=\frac{\sum_{t=1}^{T-1}P(O,i^{(t)}=i,i^{(t+1)}=j|\hat{\lambda})}{\sum_{t=1}^{T-1}P(O,i^{(t)}=i|\hat{\lambda})} \\ b_j(n)=\frac{\sum_{t=1}^{T}P(O,i^{(t)}=j|\hat\lambda)I(o_t=v_n)}{\sum_{t=1}^{T}P(O,i^{(t)}=j|\hat\lambda)}
π(i)=P(O∣λ^)P(O,i(2)=i∣λ^)aij=∑t=1T−1P(O,i(t)=i∣λ^)∑t=1T−1P(O,i(t)=i,i(t+1)=j∣λ^)bj(n)=∑t=1TP(O,i(t)=j∣λ^)∑t=1TP(O,i(t)=j∣λ^)I(ot=vn)
我们再次回顾一下第1章中通过前向和后向计算得到的衍生公式:
γ
t
(
i
)
=
P
(
q
t
=
σ
i
∣
O
,
λ
)
=
α
t
(
i
)
β
t
(
i
)
∑
j
M
α
t
(
j
)
β
t
(
j
)
ξ
t
(
i
,
j
)
=
P
(
q
t
=
σ
i
,
q
t
+
1
=
σ
j
∣
O
,
λ
)
=
α
t
(
i
)
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
∑
s
M
∑
r
M
α
t
(
s
)
a
s
r
b
r
(
o
t
+
1
)
β
t
+
1
(
r
)
\begin{aligned} \gamma_t(i) & =P(q_t=\sigma_i|O,\lambda)=\frac{\alpha_t(i)\beta_t(i)}{\sum_j^M\alpha_t(j)\beta_t(j)} \\ \xi_t(i,j) & =P(q_t=\sigma_i,q_{t+1}=\sigma_j|O,\lambda)=\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_s^M\sum_r^M\alpha_t(s)a_{sr}b_r(o_{t+1})\beta_{t+1}(r)} \end{aligned}
γt(i)ξt(i,j)=P(qt=σi∣O,λ)=∑jMαt(j)βt(j)αt(i)βt(i)=P(qt=σi,qt+1=σj∣O,λ)=∑sM∑rMαt(s)asrbr(ot+1)βt+1(r)αt(i)aijbj(ot+1)βt+1(j)
因此我们结合推导出来的衍生公式可以将(57)公式集合转换为更加简洁的形式,其中
a
i
j
a_{ij}
aij和
b
j
(
n
)
b_j(n)
bj(n)的推导中上下分子分母同除
P
(
O
∣
λ
^
)
P(O|\hat{\lambda})
P(O∣λ^):
π
(
i
)
=
γ
2
(
i
)
a
i
j
=
∑
t
=
1
T
−
1
ξ
t
(
i
,
j
)
∑
t
=
1
T
−
1
γ
t
(
i
)
b
j
(
n
)
=
∑
t
=
1
,
o
t
=
v
n
T
γ
t
(
j
)
∑
t
=
1
T
γ
t
(
j
)
\pi(i)=\gamma_2(i) \\ a_{ij}=\frac{\sum_{t=1}^{T-1}\xi_t(i,j)}{\sum_{t=1}^{T-1}\gamma_t(i)} \\ b_j(n)=\frac{\sum_{t=1,o_t=v_n}^{T}\gamma_t(j)}{\sum_{t=1}^{T}\gamma_t(j)}
π(i)=γ2(i)aij=∑t=1T−1γt(i)∑t=1T−1ξt(i,j)bj(n)=∑t=1Tγt(j)∑t=1,ot=vnTγt(j)





















 782
782











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








