从偏微分角度理解神经网络的反向传播

神经网络结构

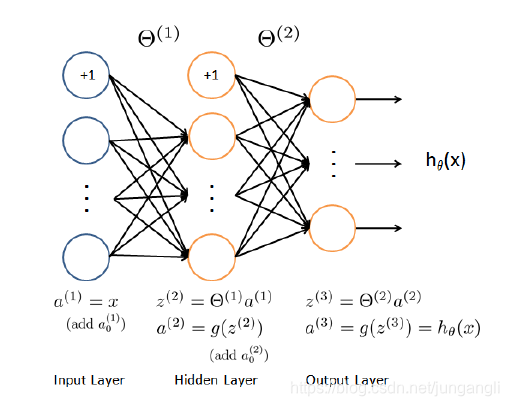
这里我们以3层神经网络为例，来分析反向传播的过程，结构图如下：

3层神经网络结构图

这里的每一个神经元的计算都可以理解为一次逻辑回归的计算过程，其中:
$h_{\theta }(x)=g({\theta }^T\ast x)$
$g(z)=\frac{1}{(1+e^{-z})}$
$g^{\prime }(z)=g(z)\ast (1-g(z))$
所以：
$$h_{\theta }(x)=\frac{1}{(1+e^{-{\theta }^T\ast x})}$$
神经网络的代价函数如下：
$$J(\theta )=1/m\ast \sum _{i=1}^m\sum _{k=1}^K[-y_k^{(i)}log((h_{\theta }(x^{(i)}){)}_k)-(1-y_k^{(i)})log(1-(h_{\theta }(x^{(i)}){)}_k]$$

这里是不带正则化的代价函数$Cost(i)$，它与逻辑回归的代价函数很相似。
这里的k表示第k个输出类别，因为神经网络输出层有$K$个神经元 。

理解反向传播(Back Propagation)

我们这里以1个样本(i)的3层神经网络来分析, 1个输入层,1个隐藏层，1个输出层。
其实反向传播就是计算代价函数对每一层的${\theta }_{ij}$参数的偏微分，和之前的逻辑回归算法类似，用这些偏微分进行梯度下降求代价函数的最小值。
那么代价函数可以简化为：
$$J(\theta )=-ylog(a^{(3)})-(1-y)log(1-a^{(3)})$$
$$J(\theta )=-ylog(g(z^{(3)}))-(1-y)log(1-g(z^{(3)}))$$

其中$y$和$a^{(3)}$都是向量，维度为K，表示K个输出神经元

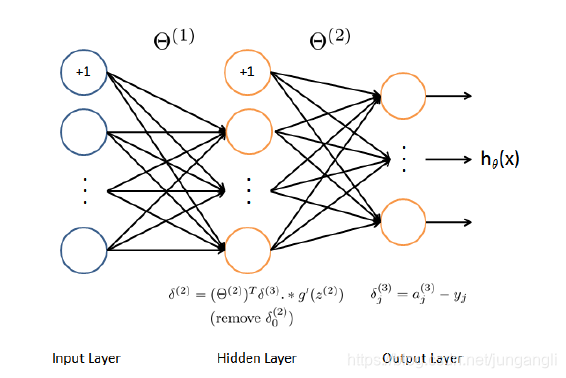
反向传播推导过程

从后往前推导，首先计算代价函数对第2层$\theta$的偏微分，可以表示为：
$$\frac{\partial J(\theta )}{\partial {\theta }_{ij}^{(2)}}=\frac{\partial J(\theta )}{\partial z_j^{(3)}}\ast \frac{\partial z_j^{(3)}}{\partial {\theta }_{ij}^{(2)}}$$
$\because \frac{\partial J(\theta )}{\partial z_j^{(3)}}=\frac{\partial J(\theta )}{\partial a_j^{(3)}}\ast \frac{\partial a_j^{(3)}}{\partial z_j^{(3)}}=g(z_j^{(3)})-y_j=a_j^{(3)}-y_j$

$\because \frac{\partial z_j^{(3)}}{\partial {\theta }_{ij}^{(2)}}=(a_j^{(2)}{)}^T$

所以，代价函数对第2层$\theta$的偏微分：
$$\frac{\partial J(\theta )}{\partial {\theta }_{ij}^{(2)}}=(a_j^{(3)}-y_j)\ast (a_j^{(2)}{)}^T$$

这里我们引入一个${\delta }^{(l)}$项，它表示代价函数对每一层上的$z^{(l)}$的偏导数，所以前面我们推导的：
${\delta }_j^{(3)}=\frac{\partial J(\theta )}{\partial z_j^{(3)}}=a_j^{(3)}-y_j$

$l$表示层数；
${\delta }_j^{(3)}$表示代价函数$J(\theta )$对$z_j^{(3)}$的偏导数；
以此类推，${\delta }_j^{(2)}$就表示代价函数$J(\theta )$对$z_j^{(2)}$的偏导数。

接下来我们计算代价函数对第1层$\theta$的偏微分，可以表示为：
$$\frac{\partial J(\theta )}{\partial {\theta }_{ij}^{(1)}}=\frac{\partial J(\theta )}{\partial z_j^{(2)}}\ast \frac{\partial z_j^{(2)}}{\partial {\theta }_{ij}^{(1)}}$$

$\because \frac{\partial J(\theta )}{\partial z_j^{(2)}}=\frac{\partial J(\theta )}{\partial a_j^{(2)}}\ast \frac{\partial a_j^{(2)}}{\partial z_j^{(2)}}=\frac{\partial J(\theta )}{\partial a_j^{(2)}}\ast g^{\prime }(z_j^{(2)})=\frac{\partial J(\theta )}{\partial z_j^{(3)}}\ast \frac{\partial z_j^{(3)}}{\partial a_j^{(2)}}\ast g^{\prime }(z_j^{(2)})$

$\because {\delta }_j^{(3)}=\frac{\partial J(\theta )}{\partial z_j^{(3)}}$

$\because z_j^{(3)}={\Theta }_j^{(2)}\ast a_j^{(2)}$

$\therefore \frac{\partial z_j^{(3)}}{\partial a_j^{(2)}}=({\Theta }_j^{(2)}{)}^T$

$\therefore {\delta }_j^{(2)}=\frac{\partial J(\theta )}{\partial z_j^{(2)}}=({\Theta }_j^{(2)}{)}^T\ast {\delta }_j^{(3)}\ast g^{\prime }(z_j^{(2)})$

$\because \frac{\partial z_j^{(2)}}{\partial {\theta }_{ij}^{(1)}}=(a_j^{(1)}{)}^T$

所以代价函数对第1层$\theta$的偏微分：
$$\frac{\partial J(\theta )}{\partial {\theta }_{ij}^{(1)}}=({\Theta }_j^{(2)}{)}^T\ast {\delta }_j^{(3)}\ast g^{\prime }(z_j^{(2)})\ast (a_j^{(1)}{)}^T$$

最后累加每个样本在每一层的偏微分：
$${\Delta }_{(ij)}^{(l)}={\Delta }_{(ij)}^{(l)}+a_j^{(l)}\ast {\delta }_i^{(l+1)}$$