
总第239篇/张俊红
前面我们讲了T检验、F检验、Q检验等。这一篇来讲讲似然比检验。在讲似然比检验之前,我们先讲两个与似然比相关的概念:似然函数与极大似然估计。
似然函数
说到似然函数,就不得不说一下似然性了,似然性是与概率相对应的一个概念。概率用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而似然性则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计。
我们知道正态分布的概率密度函数的中主要有两个参数:均值和标准差。如果我们知道了数据服从正态分布,也知道该分布对应的均值和标准差,这个时候我们就知道每个值发生的可能性,这就是概率;如果我们不知道分布对应的均值和标准差,但是可以观测到已经发生的一些值,那么通过已经观测到的结果值对分布对应的均值和标准差进行估计的过程就是似然性。
已经观测到的值x与要估计的参数θ之间会构造出来一个函数,这个函数就是似然函数:L(θ|x)。
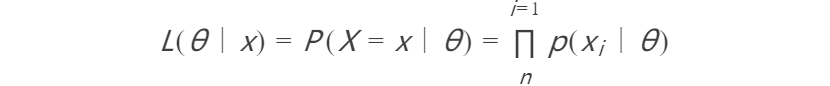
似然函数L(θ|x)(在数值上)等于给定参数θ后变量X整体观测结果的概率,等于每一个x取值的概率乘积。
如果已知了变量x的分布,那么每个x发生的概率就是其概率密度函数得出。
极大似然估计
知道什么是似然函数以后,我们再来看看什么是极大似然估计。用一句话来描述就是:极大似然估计是求取使观测到的结果概率P(X = x|θ)最大化时对应的参数θ的取值。
其实就是求似然函数L(θ|x)最大时对应的θ值,我们知道,要求最值,一般都是对函数求导即可,这里对函数L(θ|x)求导,即可得到θ值。
似然比检验
了解完似然函数和极大似然估计以后,我们再来看我们今天的主题,似然比检验。
似然比检验和其他检验思想比较类似,似然比检验的核心是根据似然比这个统计量来进行判断,其他检验是根据其他统计量来进行判断,比如t检验是根据t统计量来进行判断。
似然比检验的原假设H0是:θ=θ0,备择假设H1:θ=θ1,其中θ0是θ1的子集。
似然比的公式如下:

似然比表示θ取不同值对应的似然函数的比值。如果λ很大,说明参数θ=θ1时对应的似然性要比θ=θ0时对应的似然性大。此时,更倾向于拒绝H0假设;反之,若此值较小,说明参数θ=θ0时对应的似然性要比θ=θ1时对应的似然性大,更倾向于接受H0假设。
那λ到底大于多少算大,小于多少算小呢?这个时候就需要有个临界值λ0,如果λ>λ0,那么就拒绝H0假设。
接下来的问题就是求取λ0,要临界值λ0,必须知道当H0成立时λ的分布,当n足够大时,λ是服从卡方分布的,知道分布,然后再根据显著性水平α就可以计算出临界值了。
以上就是关于似然比检验相关的内容。









 本文深入探讨了似然比检验的原理,包括似然函数、极大似然估计及似然比检验的应用。似然函数用于估计未知参数,极大似然估计则寻找使观测结果概率最大的参数值。似然比检验通过比较不同参数假设下的似然性,判断原假设是否成立。
本文深入探讨了似然比检验的原理,包括似然函数、极大似然估计及似然比检验的应用。似然函数用于估计未知参数,极大似然估计则寻找使观测结果概率最大的参数值。似然比检验通过比较不同参数假设下的似然性,判断原假设是否成立。

















 4725
4725

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










