选址问题梳理汇总

最近论文涉及到选址问题，于是疯狂看各种文献，特别是网上各种博客、论坛中关于选址问题的解释。在这里结合我的研究一并讨论于此。部分内容属于网上转载。

---

设施选址问题（Facility Location Problem）自20世纪60年代初期以来，在运筹学中一直占据着中心位置。它来自于工厂、仓库、超市、学校、医院、图书馆、火车站、代理服务器、传感器等位置的确定问题。

　　设施选址问题是NP-难解问题，除非P=NP，设施选址问题不存在多项式时间算法。

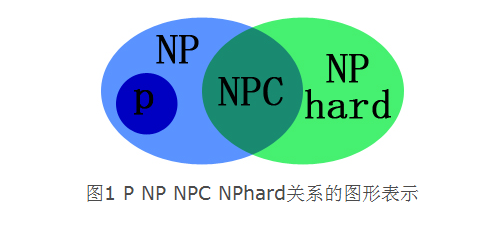
　　P问题：

　　一个问题可以在多项式（O(n^k)）的时间复杂度内解决。

　　NP问题：

　　一个问题的解可以在多项式的时间内被验证。

　　NP-hard问题：

　　任意NP问题都可以在多项式时间内归约为该问题，但该问题本身不一定是NP问题。归约的意思是为了解决问题A，先将问题A归约为另一个问题B，解决问题B同时也间接解决了问题A。

　　NPC问题：

　　既是NP问题，也是NP-hard问题。

　　已知一个 极小化问题，如果算法在多项式时间内能给出可行解，并且所对应的目标值不超过最优值的? (≥ ?)倍，那么称该算法为 ?-近似算法，称?为 近似比。

设施选址问题的近似算法主要分三类：

　　1. LP rounding 

　　线性规划舍入法：首先给出原问题的线性整数规划模型，然后求解相应的线性规划松弛问题得到分数最优解，根据可行要求对分数最优解进行改造，构造原问题的整数可行解，属于非组合算法。

　　2. Primal-Dual

　　原始对偶法：设计组合算法给出对偶问题的可行解，根据该对偶可行解构造原始问题的整数可行解。

　　3. Local Search

　　局部搜索法：给定初始可行解，定义适当的邻域，通过引入恰当的调整策略，在邻域中得到改进的可行解，依次迭代，直到调整策略不能改进为止。

1. 选址的意义

　　

　　

2. 选址问题的程序和步骤

1. 选址约束条件分析
2. 搜索整理资料
3. 地址筛选
4. 定量分析
5. 结果评价
6. 复查和确定选址

　　

选址约束条件分析

　　（1）需求条件

　　顾客现在分布，未来分布预测，货物作业量的增长率及物流区域分析。货物作业量也可以是其他的流量或流动的对象。

　　（2）运输条件

　　北京市的四道口蔬菜、果品配送中心就建在铁路货运站旁边，并且近靠公路。

　　即采取什么样的运输方式，陆运还是空运，等等。

　　（3）配送服务的条件

　　向顾客报告到会时间、发送频率、根据供货时间计算的从顾客到物流重心的距离和服务范围等。

　　（4）用地条件

　　（5）法规

收集整理资料

　　为正确构造优化模型必须：
　　（1）掌握业务量
　　　　①工厂到物流中心之间的运输量。即从上一级到本级的流量，R3-R2之间。
　　　　②向顾客配送的货物数量。从本级到下一级的流量，或反之，R2-R1之间。
　　　　③物流中心保管的货物数量
　　（2）掌握费用（衡量指标）
　　　　①工厂至配送中心之间的运输量
　　　　②物流中心到顾客之间的配送费
　　　　③与设施、土地有关的费用及人工费、业务费等
　　① ②两项费用，随着业务量和运送距离的变化而变动，所以必须对每一吨公里的费用进行分析（成本分析）； ③项包括可变费用和固定费用&#