深度学习中的一些概念------epochs，batch，iterations，Mini-batch gradient descent, 前向传播，反向传播

1，epochs，batch，iterations

1，epochs

1个epoch等于使用全部训练数据训练一次，也可以说1个epoch是整个输入数据的单次向前和向后传递。

epoch的值就是同样的一个全部训练数据集被重复用几次来训练，亦即应当完整遍历训练数据集多少次。

2，batch

把全部训练数据分为若干个批(batch），按批来更新参数(拿到一批样本点的error之后才去update参数)。既不是像Batch gradient descent(批梯度下降)那样,遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，更新梯度。也不是像stochastic gradient descent(随机梯度下降)那样,每看一个数据就算一下损失函数，然后求梯度更新参数。

batch_size就是1个batch包含的样本的数目. batchsize最大是样本总数N，此时就是Full batch learning,亦是Batch gradient descent；最小是1，即每次只训练一个样本，这就是在线学习（Online Learning）,亦是stochastic gradient descent。

3，iterations

1个iteration等于使用batch_size个样本训练一次；每一次迭代都是一次权重更新，每一次权重更新需要batch_size个数据进行Forward运算得到损失函数，再BP算法更新参数。

总结:

https://blog.csdn.net/qq_37274615/article/details/81147013

one epoch = numbers of iterations = 训练样本的数量/batch_size

实际上，梯度下降的几种方式的根本区别就在于上面公式中的 Batch Size不同。

*注：上表中 Mini-Batch 的 Batch 个数为 N / B + 1 是针对未整除的情况。整除则是 N / B。

实例:

mnist 数据集有 60000 张图片作为训练数据，10000 张图片作为测试数据。假设现在选择  Batch Size = 100 对模型进行训练。迭代30000次。https://blog.csdn.net/xiaohuihui1994/article/details/80624593

1. 每个 Epoch 要训练的图片数量：60000(训练集上的所有图像)
2. 训练集具有的 Batch 个数： 60000/100=600
3. 每个 Epoch 需要完成的 Batch 个数： 600
4. 每个 Epoch 具有的 Iteration 个数： 600（完成一个Batch训练，相当于参数迭代一次）
5. 每个 Epoch 中发生模型权重更新的次数：600
6. 训练 10 个Epoch后，模型权重更新的次数： 600*10=6000
7. 不同Epoch的训练，其实用的是同一个训练集的数据。第1个Epoch和第10个Epoch虽然用的都是训练集的60000图片，但是对模型的权重更新值却是完全不同的。因为不同Epoch的模型处于代价函数空间上的不同位置，模型的训练代越靠后，越接近谷底，其代价越小。
8. 总共完成30000次迭代，相当于完成了 30000/600=50 个Epoch

2,前向传播和反向传播

1，前向传播Forward propagation

前向传播就是网络如何根据输入X得到输出Y,并根据输出Y和损失函数得到loss.

2，反向传播Back propagation

反向传播就是网络通过最小化损失值loss来不断调整参数的过程.

3, Mini-batch gradient descent

1,小批量梯度下降步骤

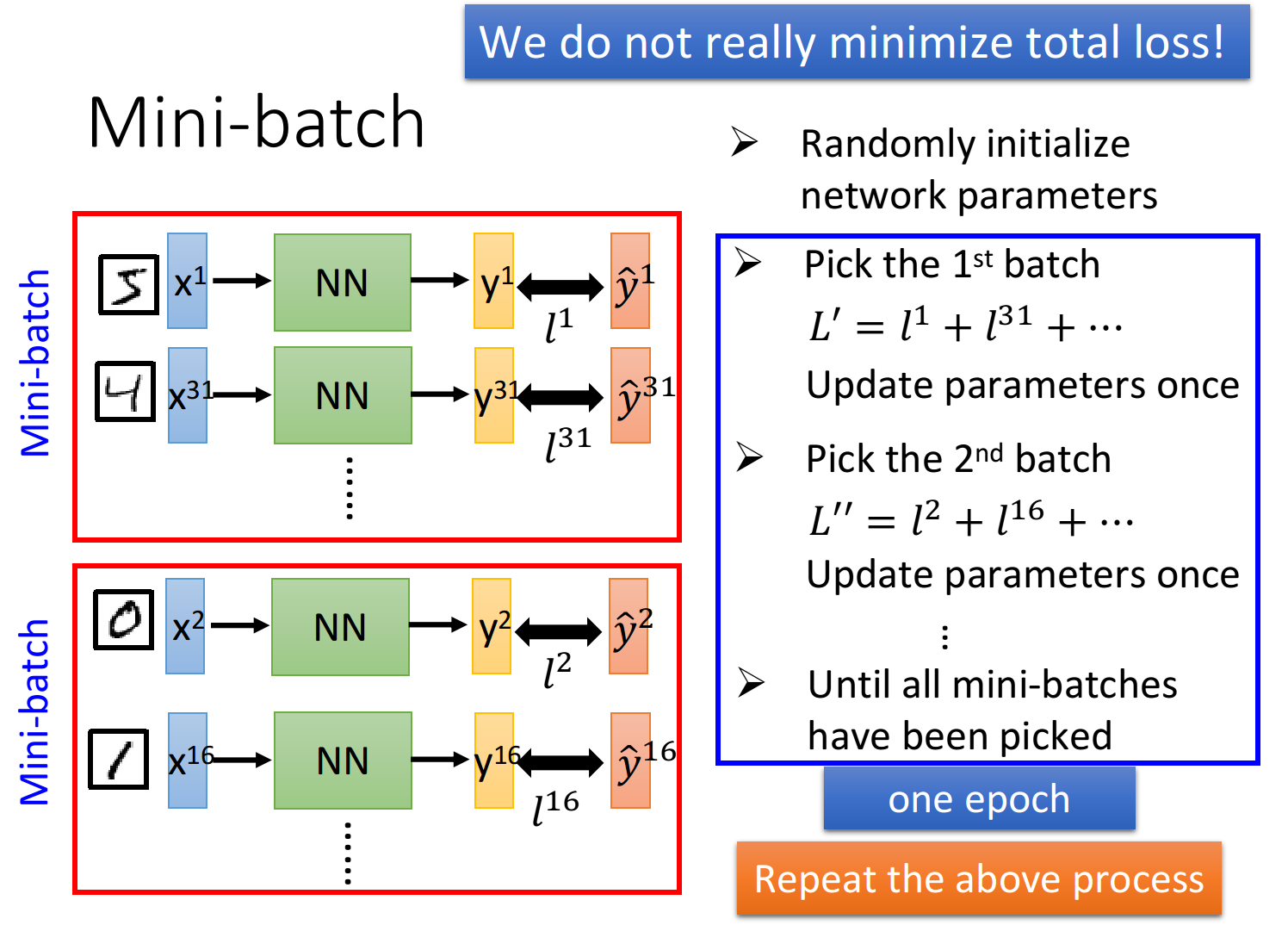
2, Batch size and Training Speed

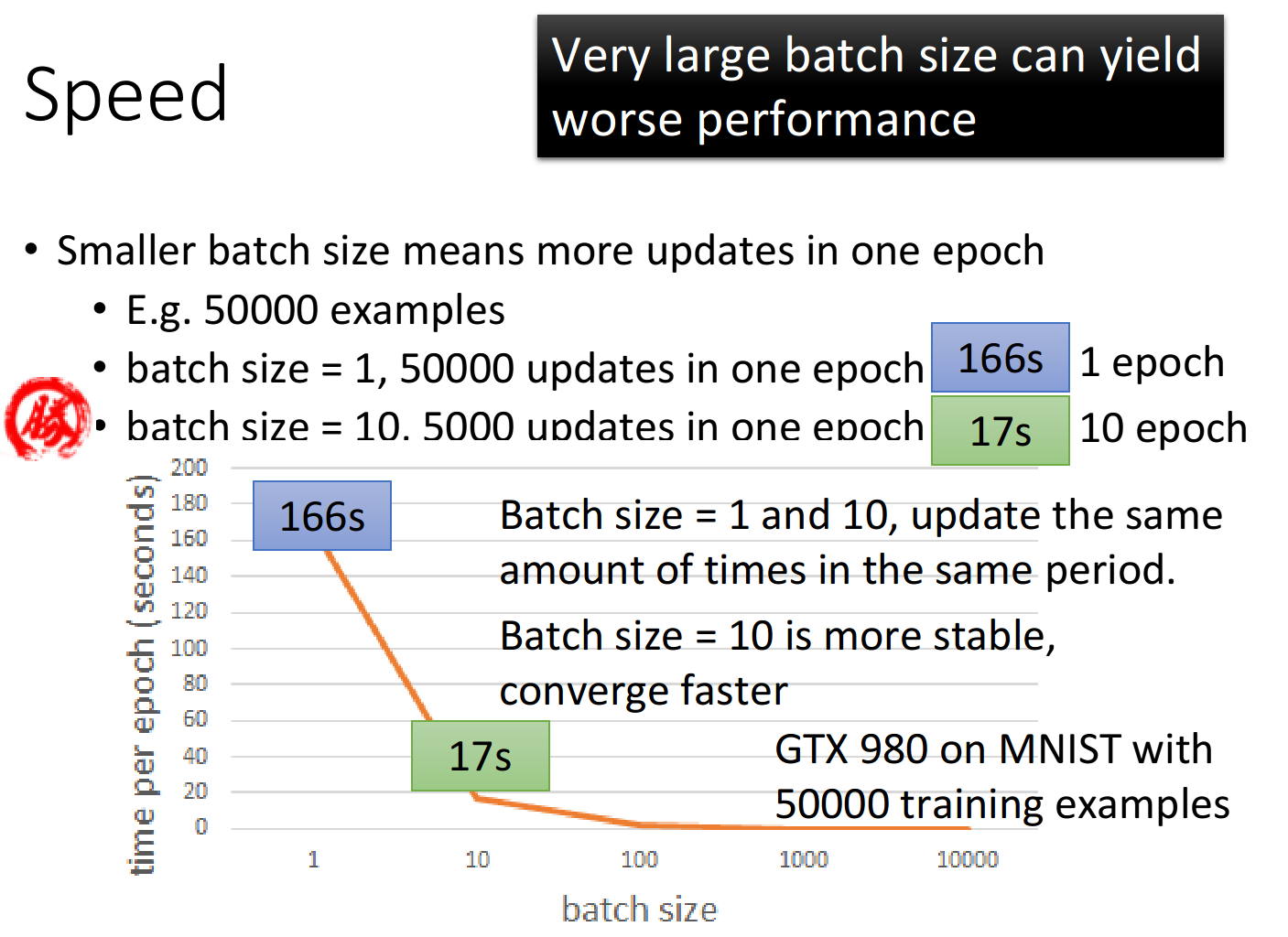
batch size会受到GPU平行加速的限制，太大可能导致在train的时候卡住

上面例子batch size设为10的一个epoch所需时间那么少的现象产生的原因是我们用了GPU，用了平行运算，所以batch size=10的时候，这10个example其实是同时运算的，所以你在一个batch里算10个example的时间跟算1个example的时间几乎可以是一样的.

如果你用的batch size很大，甚至是Full batch，那你走过的路径会是比较平滑连续的，可能这一条平滑的曲线在走向最低点的过程中就会在坑洞或是缓坡上卡住了；但是，如果你的batch size没有那么大，意味着你走的路线没有那么的平滑，有些步伐走的是随机性的，路径是会有一些曲折和波动的.

如下图，左边是full batch(拿全部的Training data做一个batch)的梯度下降效果，可以看到每一次迭代成本函数都呈现下降趋势，这是好的现象，说明我们w和b的设定一直再减少误差， 这样一直迭代下去我们就可以找到最优解；右边是mini batch的梯度下降效果，可以看到它是上下波动的，成本函数的值有时高有时低，但总体还是呈现下降的趋势， 这个也是正常的，因为我们每一次梯度下降都是在min batch上跑的而不是在整个数据集上， 数据的差异可能会导致这样的波动(可能某段数据效果特别好，某段数据效果不好)，但没关系，因为它整体是呈下降趋势的

 

再看下面的图：蓝色部分是full batch而紫色部分是mini batch，就像上面所说的mini batch不是每次迭代损失函数都会减少，所以看上去好像走了很多弯路，不过整体还是朝着最优解迭代的，而且由于mini batch一个epoch就走了5000步(5000次梯度下降)，而full batch一个epoch只有一步，所以虽然mini batch走了弯路但还是会快很多.

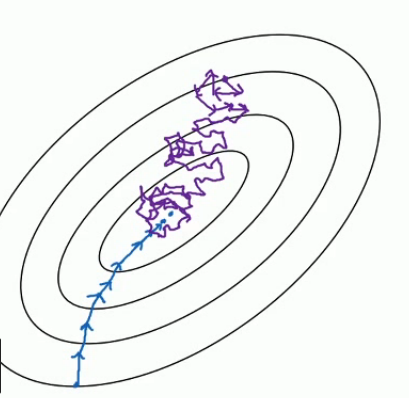
因此batch size既不能太大，因为它会受到硬件GPU平行加速的限制，导致update次数过于缓慢，并且由于缺少随机性而很容易在梯度下降的过程中卡在saddle point或是local minima的地方(极端情况是Full batch)；而且batch size也不能太小，因为它会导致速度优势不明显的情况下，梯度下降曲线过于不稳定，算法可能永远也不会收敛(极端情况是Stochastic gradient descent).

4,常用梯度下降法（BGD，SGD，MBGD）

https://www.cnblogs.com/pinard/p/5970503.html

1,批量梯度下降法（Batch Gradient Descent）

在更新参数时使用所有的样本来进行更新, 我们有m个样本，那么求梯度的时候就用了所有m个样本的梯度数据。

2,随机梯度下降法（Stochastic Gradient Descent）

求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本来求梯度。随机梯度下降法，和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个只用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

3,小批量梯度下降法（Mini-batch Gradient Descent）

小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于m个样本，我们采用x个样子来迭代，1<x<m。一般可以取x=10，当然根据样本的数据，可以调整这个x的值, x就是batch_size。