本文通过0-1背包问题的不同解法,深入理解计算机常用算法动态规划、贪心、回溯、分支限界法的思想。
问题描述
0-1背包问题:给定n种物品和一背包。物品i的重量是wi,其价值是vi,背包的容量为C。问:应该如何选择装入背包的物品,使得装入背包中物品的总价值最大?
简单n=3的例子:设w=[16,15,15],v=[45,25,25],c=30
1.动态规划解0-1背包问题
分析
(1)0-1背包问题是求在以下条件下
1)∑wi*xi<=C, i from 1 to n
2)xi∈{0,1},1<=i<=n
总价值最大,
即∑vi*xi最大, i from 1 to n
(2)最优子结构性质
若(x1,x2…xn)是0-1背包的最优解,则(x1,x2…xn-1)是下面相应子问题的最优解。
1)∑wi*xi<=C-wn*xn, i from 1 to n-1
2)xi∈{0,1},1<=i<=n-1
总价值最大,
即∑vi*xi最大, i from 1 to n-1
可用反证法证明,证明略。
(3)递归关系
设m[i][j]为选择前i个物品,容量为j能装入物品价值的最大值。
可得如下递归关系
1)当 0<=j<wi 时,m[i][j]=m[i-1][j];
2)当 j>=wi时,m[i][j]=max{m[i-1][j],m[i-1][j-wi]+vi};
递推关系是这么形成的:
通过选择第i件物品放或不放来形成递推关系,
1)如果不放第i件物品,问题就转化为“前i-1件物品放入容量为c的背包中”,价值为m[i -1][j];
2)如果放第i件物品,那么问题就转化为“前i -1件物品放入剩下的容量为v-Ci的背包中“,价值为m[i-1][j-wi]+vi
而m[n][c]为选择前n个物品,容量为c背包能装入物品价值的最大值。
代码如下
#include <stdio.h>
int m[100][100];
int dp_knapsack(int w[], int v[], int c, int m[][100],int n)//m[i][j]表示背包可选物品为1,2,..i,容量为j时的最优解
{
//初始化
int i, j;
for (j = 1; j <= c; j++)
{
m[1][j] = 0;
}
for (j = w[0]; j <= c; j++)
{
m[1][j] = v[0];
}
//循环直到求出m[n][c]
for (i = 2; i <= n; i++)
{
for (j = 1; j <= c; j++)
{
if (j < w[i - 1])
{
m[i][j] = m[i - 1][j];
}else
{
if (m[i - 1][j]>=(m[i - 1][j - w[i - 1]] + v[i - 1]))
{
m[i][j] = m[i - 1][j];
}else
{
m[i][j] = m[i - 1][j - w[i - 1]] + v[i - 1];
}
}
}
}
return 0;
}
int main()
{
int weight[3] = { 16, 15, 15 };
int value[3] = { 45, 25, 25 };
int c =30;
dp_knapsack(weight, value, c,m,3);
printf("%d", m[3][30]);
}2.贪心法求0-1背包问题
贪心法的思路是先求每个物品单位重量的价值,按单位重量的价值从大到小排序。然后按这个顺序往背包里面放物品。
注意,贪心法不能解这个n=3,weight[3] = { 16, 15, 15 };value[3] = { 45, 25, 25 }的0-1背包问题。因为依照贪心选择策略,首先将1物品装入,得到的最大值为45。而实际上选择2,3物品能得到最大价值为50。
3.回溯法求0-1背包问题
分析
回溯法是一个带有系统性和跳跃性的搜索算法。它在问题的解空间树中,按深度优先策略,从根节点出发搜索空间树。
如以上背包问题,当n=3时,解空间为:
{(0,0,0),(0,1,0),(0,0,1),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)}
如图为0-1背包的解空间树:
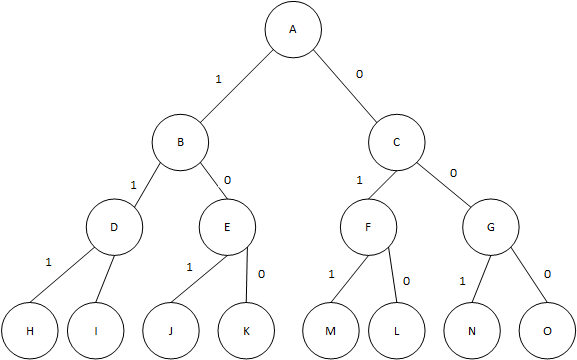
按深度优先搜索,A-B-K为一个可行路径,此时maxValue=45,
继续搜索,A-C-F-M为一个可行路径,此时maxValue=50;
遍历所有路径,得到maxValue=50;
#include <stdio.h>
#include <stdlib.h>
int bestValue=0,curWeight=0,curValue=0;
int backtrack_knapsack(int w[], int v[], int c, int n,int i)
{
if (i > n)
{
if (curValue > bestValue)
{
bestValue = curValue;
}
return 0;
}
if (curWeight + w[i - 1]<=c)//搜索左子树
{
curWeight += w[i - 1];
curValue += v[i - 1];
backtrack_knapsack(w, v, c, n, i + 1);
curWeight -= w[i - 1];
curValue -=v[i - 1];
}
backtrack_knapsack(w, v, c, n, i + 1);//搜索右子树
return 0;
}
int main()
{
int weight[3] = { 16, 15, 15 };
int value[3] = { 45, 25, 25 };
int c =30;
backtrack_knapsack(weight, value, c, 3, 1);
printf("%d\n", bestValue);
}4.分支限界法求0-1背包问题
4.1分支限界法介绍
分支限界法类似于回溯法,是在解空间树上搜索问题解的算法。
分支限界法的搜索策略是,在扩展结点处,先生成其所有的儿子结点(分支),然后再从当前活结点表中选出下一个扩展结点。为了有效的选择下一扩展结点,加速搜索过程,在每一活结点出,计算一个函数值(限界),并根据函数值,从当前结点表中选择一个最有利的结点作为扩展结点。
分支限界常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。
分析
4.2采用队列式分支限界法解0-1背包问题
队列式分支限界法将活结点表组织成一个队列,并按队列的先进先出原则选取下一个结点为当前扩展结点。
分析
如0-1背包解空间树图
每次选取队列的最前面的结点为活结点。
1)算法从根结点A开始,初始时活结点队列为空,A入队列。
2)A为活结点,A的儿子结点B、C为可行结点。将B、C加入队列,舍弃A。此时队列元素为C-B;
3)B为活结点,B的儿子结点D、E,而D为不可行结点。将E入队列,舍弃B。此时队列元素为E-C;
4)循环以上步骤
按照以上方式扩展到叶节点。
K为一个可行的叶节点,表示一个可行解,价值为45。
L为一个可行的叶节点,表示一个可行解,价值为50…
最后活结点队列为空,算法终止。
以下代码-1的作用主要有两个,(a)用来标记树的每一层。(b)保证队列不为空,当为空时循环结束。
代码如下:
#include<iostream>
#include<queue>
using namespace std;
typedef struct treenode{
int weight;
int value;
int level;
int flag;
}treenode;
queue<struct treenode> que;
int enQueue(int w,int v,int level,int flag,int n,int* bestvalue)
{
treenode node;
node.weight = w;
node.value = v;
node.level = level;
node.flag = flag;
if (level == n)
{
if (node.value > *bestvalue)
{
*bestvalue = node.value;
}
return 0;
}else
{
que.push(node);
}
}
//w为重量数组,v为价值数组,n为物品个数,c为背包容量,bestValue为全局最大价值
int bbfifoknap(int w[],int v[],int n,int c,int* bestValue)
{
//初始化结点
int i=1;
treenode tag, livenode;
livenode.weight = 0;
livenode.value = 0;
livenode.level = 1;
livenode.flag = 0;//初始为0
tag.weight = -1;
tag.value = 0;
tag.level = 0;
tag.flag = 0;//初始为0
que.push(tag);
while (1)
{
if (livenode.weight + w[i - 1] <= c)
{
enQueue(livenode.weight + w[i - 1], livenode.value + v[i - 1], i, 1,n,bestValue);
}
enQueue(livenode.weight,livenode.value, i, 0,n,bestValue);
livenode = que.front();
que.pop();
if (livenode.weight == -1)
{
if (que.empty() == 1)
{
break;
}
livenode = que.front();
que.pop();
que.push(tag);
i++;
}
}
return 0;
}
int main()
{
int w[] = { 16, 15, 15 };
int v[] = { 45, 25, 25 };
int n = 3;
int c = 30;
int bestValue=0;
bbfifoknap(w, v,n,c,&bestValue);
cout << bestValue<<endl;
return 0;
}4.3采用优先队列式分支限界法解0-1背包问题
优先队列分支限界法将活结点表组织成优先队列,并按优先队列中规定的
结点优先级选取最高的下一个结点成为当前扩展结点。
分析
如0-1背包解空间树图
选取结点的价值为规定的优先级。
每次选取优先级最高的结点为活结点。
1)算法从根结点A开始,初始时活结点队列为空,设A为活结点。
2)A为活结点,A的儿子结点B、C为可行结点。将B、C加入优先级队列。此时优先级队列元素为C-B;
3)B为活结点,B的儿子结点D、E,而D为不可行结点。将E入优先级队列,舍弃B。此时队列元素为C-E;
4)E为活结点,舍弃B。E的儿子结点J、K,J为不可行结点。由于到了树的最后一层,K不用入队列,K为一个可行的叶节点,表示一个可行解,价值为45。
5)C为活结点,舍弃C。F,G为儿子结点,为可行结点,入优先级队列。此时队列元素为F,G。
6)循环以上步骤,直到优先队列为空。
#include<iostream>
#include<queue>
using namespace std;
struct treenode{
int weight;
int value;
int level;
int flag;
friend bool operator< (treenode a, treenode b)
{
return a.value < b.value;
}
};
priority_queue<treenode> prique;
void enPriQueue(int weight,int value,int level,int flag,int n,int* bestValue)
{
treenode node;
node.weight = weight;
node.value = value;
node.level = level;
node.flag = flag;
if (level == n)
{
if (value > *bestValue)
{
*bestValue = value;
}
return;
}else
{
prique.push(node);
}
return;
}
//
int prioritybbnap(int w[],int v[],int c,int n,int* bestValue)
{
treenode liveNode;
liveNode.weight = 0;
liveNode.value = 0;
liveNode.level = 0;
liveNode.flag = 0;
prique.push(liveNode);
do
{
if (liveNode.weight + w[liveNode.level] <= c)
{
enPriQueue(liveNode.weight + w[liveNode.level], liveNode.value + v[liveNode.level],
liveNode.level + 1, 1,n,bestValue);
}
enPriQueue(liveNode.weight, liveNode.value, liveNode.level + 1, 0, n, bestValue);
liveNode = prique.top();
prique.pop();
} while (!prique.empty());
return 0;
}
int main()
{
int w[] = { 16, 15, 15 };
int v[] = { 45, 25, 25 };
int c = 30;
int n = 3;
int bestValue=0;
prioritybbnap(w, v, c,n,&bestValue);
cout << bestValue << endl;
return 0;
}





















 787
787

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








