gDLPCA
参考论文:Graph-dual Laplacian principal component analysis
作者:Jinrong He · Yingzhou Bi · Bin Liu · Zhigao Zeng
思想
近年来,研究表明,高维数据不仅存在于数据空间的低维流形上,特征也存在于特征空间的流形上。然而PCA,gLPCA都忽略了特征空间中包含局部几何结构。
PCA
PCA详见本人另一篇文章【机器学习】【降维】PCA主成分分析
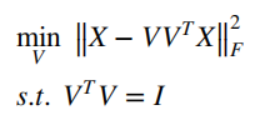
其中
X
X
X是中心化后的数据矩阵,
V
V
V是投影矩阵。
PCA的局限性:
- PCA只能识别线性子空间,不能发现非线性数据流行数据。
- 主成分的解释可能会很困难,虽然主成分分析确定的维度是作为原始特征空间的线性组合构成的不相关变量,但它们仍然没有物理意义。(为提高从PCA中提取主成分的可解释性,提出诸多变体,如:引入非负矩阵分解NMF,或采用稀疏非零载荷的SPCA)
- 对异常值敏感
gLPCA
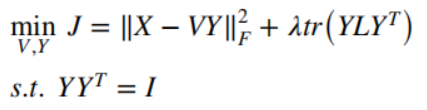
其中
λ
\lambda
λ为正则化参数,
L
=
D
−
W
L=D-W
L=D−W。
上式固定Y,对V求导:
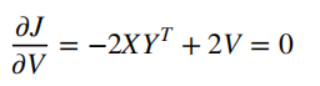
从而:
V
∗
=
X
∗
Y
T
V^*=X*Y^T
V∗=X∗YT,带回目标函数得到:
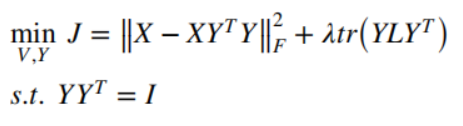
可做以下变换:

所以将目标函数转化为以下最小化公式:
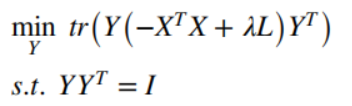
令
G
a
=
−
X
T
X
+
λ
L
G_a=-X^TX+\lambda L
Ga=−XTX+λL,于是最优的
Y
Y
Y就是
G
a
G_a
Ga的前r个最小特征值对应的特征向量组成的矩阵。
注:这里的X已经中心化
gLPCA的局限性:
- 仍然对异常值敏感
- 只考虑到数据流形,忽略特征流行
gDLPCA
X ∈ R d ∗ n X∈R^{d*n} X∈Rd∗n, d d d表示特征数, n n n表示样本数, x i x_i xi表示一列(第 i i i个样本), x j x^j xj表示一行(第 j j j个特征)
- 首先,同样与gLPCA,构造样本图
G
d
=
(
X
T
,
W
d
)
G^{d}=(X^T,W^d)
Gd=(XT,Wd):
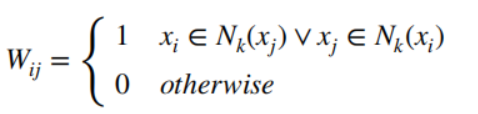
其中 N k ( x i ) N_k(x_i) Nk(xi)表示 x i x_i xi的k近邻的集合。对应的样本图拉普拉斯矩阵为 L d = D d − W d , D d = ∑ j ≠ i W i j d L^d=D^d-W^d,D^d=\sum_{j≠i}W_{ij}^d Ld=Dd−Wd,Dd=∑j=iWijd - 其次,对于{
(
x
1
)
T
,
(
x
2
)
T
,
.
.
.
,
(
x
d
)
T
{(x^1)^T,(x^2)^T,...,(x^d)^T}
(x1)T,(x2)T,...,(xd)T}构造特征图
G
f
=
(
X
T
,
W
f
)
G^{f}=(X^T,W^f)
Gf=(XT,Wf):
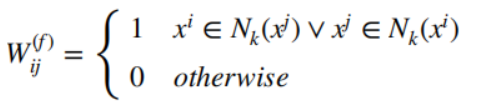
其中 N k ( x j ) N_k(x^j) Nk(xj)表示 x j x^j xj的k近邻的集合。对应的特征图拉普拉斯矩阵为 L f = D f − W f , D f = ∑ j ≠ i W i j f L^f=D^f-W^f,D^f=\sum_{j≠i}W_{ij}^f Lf=Df−Wf,Df=∑j=iWijf - gDLPCA
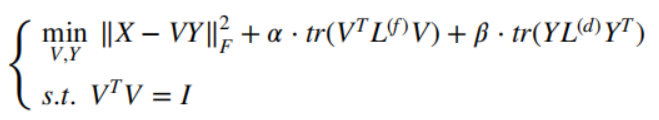
其中, α , β > 0 \alpha ,\beta>0 α,β>0都是正则化参数。当 α = 0 \alpha=0 α=0时,就是gLPCA,当 α = 0 , β = 0 \alpha=0 ,\beta=0 α=0,β=0时,就是PCA。
注意:由于上面目标函数的最优解 ( V , Y ) (V,Y) (V,Y)是不唯一的,因为上式中的迹函数的正交不变性,也就是说, ( V , Y ) (V,Y) (V,Y)是最优解,只有 ( V Q , Q T Y ) (VQ,Q^TY) (VQ,QTY)对于任意正交矩阵 Q Q Q也是最优解时,才成立,说明如下:
目标函数的第一项可以表示为:
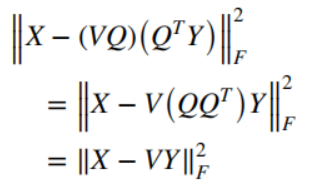
目标函数的第二项可以表示为:

显然
(
V
Q
,
Q
T
Y
)
(VQ,Q^TY)
(VQ,QTY)是最优解。
优化求解
目标函数的第一项,可被转化为:
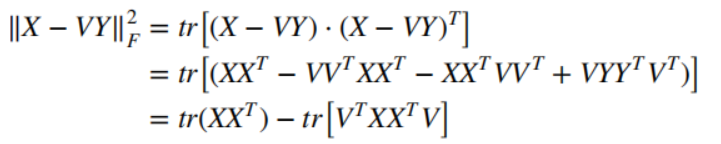
带回目标函数得到:
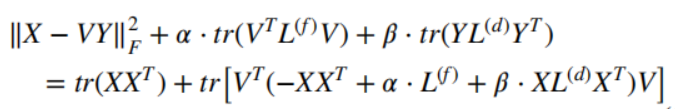
等价于:
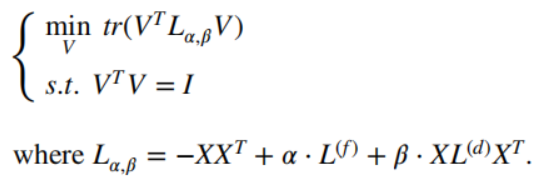
所以,可以通过求
L
α
,
β
L_{\alpha,\beta}
Lα,β的前r个最小特征值,和对应的特征向量,就可以得到最优的
V
V
V。
为了计算稳定性,协方差矩阵
X
X
T
XX^T
XXT的最大特征值(赋值给
w
n
w_n
wn)用于规范化
X
X
T
XX^T
XXT,特征图拉普拉斯矩阵
L
f
L^f
Lf的最大特征值(赋值给
α
n
\alpha_n
αn)用于规范
L
f
L^f
Lf,数据散度矩阵
X
L
d
X
T
XL^dX^T
XLdXT的最大特征值(赋值给
β
n
\beta_n
βn)用于规范化
X
L
d
X
T
XL^dX^T
XLdXT。
假设:
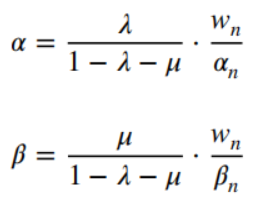
于是得到:
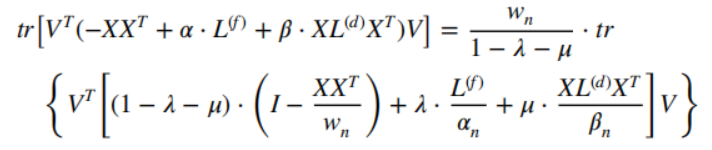
令
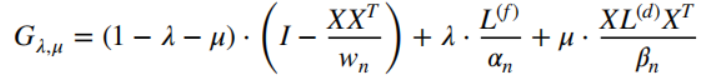
gDLPCA算法























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








