数媒笔记整理2

最近收拾资料，发现之前的数媒笔记只整理了一篇，这几天陆续补上吧。

1. 题目：2D transformation, polygon clipping, viewport

1.1. Goal

You are to write a program that receive a series of commands, and display result on screen. The commands will tell you how build your 2D world, and how to display it on screen. Your program must read the commands from a file called hw2.in.

1.2. Commands

• square: create a square in your 2D world. 即画一个正方形
• triangle: create a triangle in your 2D world. 即画一个三角形
• translate X Y: do a translation by (X, Y), multiply the current matrix by a translation matrix
• scale X Y: do a scaling by (X, Y), multiply the current matrix by a scaling matrix
• rotate X Y: do a rotation by R degree, multiply the current matrix by a rotation matrix
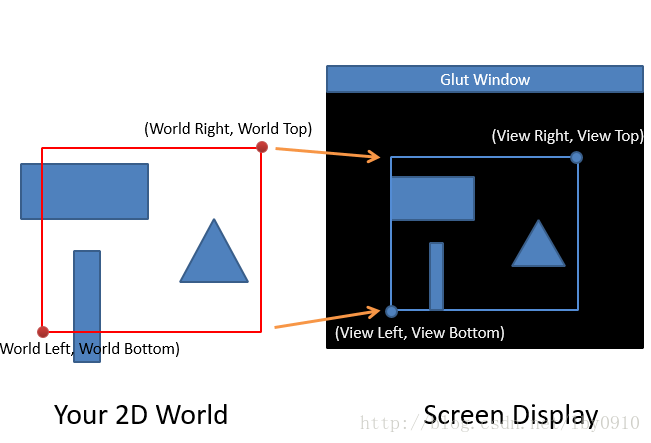
• view WL WR WB WT VL VR VB VT: WL WR WB WT (world left, world right, world bottom, world top), these 4 values specify a rectangle clip area of your 2D world. VL VR VB VT (view left, view right, view bottom, view top), these 4 values specify a viewport area in screen space.
  

1.3. Examples

# create a square and its transformation
reset
scale 2.0 2.0
rotate 45.0
translate 10.0 10.0
square
# display the world in viewports
view 0.0 20.0 0.0 20.0 100 400 100 400
end

2. 分析：

实验环境在：VS下搭配OpenGlut开发，画点和画线部分既可以用已经封装好的库函数，也可以用自己实现的画线函数。这里主要就是线性代数中的矩阵变换，根据题目要求，对矩阵实现相应的左右乘法运算。

3.源码

void Translate(float a,  float b)  {
    int i,  j,  k;
    float translation_matrix[3][3];
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            temp_matrix[i][j] = current_transform_matrix[i][j];
            current_transform_matrix[i][j] = 0;
            translation_matrix[i][j] = 0;
        }
    }
    translation_matrix[0][2] = a;
    translation_matrix[1][2] = b;
    translation_matrix[0][0] = 1;
    translation_matrix[1][1] = 1;
    translation_matrix[2][2] = 1;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            for (k = 0 ; k < 3 ; k++)  {
                current_transform_matrix[i][j] += translation_matrix[i][k] * temp_matrix[k][j];
            }
        }
    }
    cout << "After Translate, Current Transform matrix:" << endl;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            cout << current_transform_matrix[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}


void Rotate(float a)  {
    float rotation_matrix[3][3];
    int i,  j,  k;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            rotation_matrix[i][j] = 0;
            temp_matrix[i][j] = current_transform_matrix[i][j];
            current_transform_matrix[i][j] = 0;
        }
    }
    rotation_matrix[0][0] = cos((a / 180.0 * 3.14159265 ));
    rotation_matrix[0][1] = -sin((a / 180.0 * 3.14159265 ));
    rotation_matrix[1][0] = sin((a / 180.0 * 3.14159265 ));
    rotation_matrix[1][1] = cos((a / 180.0 * 3.14159265 ));
    rotation_matrix[2][2] = 1;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            for (k = 0 ; k < 3 ; k++)  {
                current_transform_matrix[i][j] += rotation_matrix[i][k] * temp_matrix[k][j];
            }
        }
    }
    cout << "After Rotate, Current Transform matrix:" << endl;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            cout << current_transform_matrix[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}


void Scale(float a,  float b)  {
    float scaling_matrix[3][3];
    int i,  j,  k;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            scaling_matrix[i][j] = 0;
            temp_matrix[i][j] = current_transform_matrix[i][j];
            current_transform_matrix[i][j] = 0;
        }
    }
    scaling_matrix[0][0] = a;
    scaling_matrix[1][1] = b;
    scaling_matrix[2][2] = 1;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            for (k = 0 ; k < 3 ; k++)  {
                current_transform_matrix[i][j] += scaling_matrix[i][k] * temp_matrix[k][j];
            }               
        }
    }
    cout << "After Scale, Current Transform matrix:" << endl;
    for (i = 0 ; i < 3 ; i++)  {
        for (j = 0 ; j < 3 ; j++)  {
            cout << current_transform_matrix[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}

4. 效果

全部源码整理之后会挂在笔者的github仓库里面：https://github.com/liby3/ComputerGraphicProject
欢迎有兴趣的童鞋一起学习。