经典的分配问题12态

提示：图片种每盒至少一球下面的范围有错误，懒得改了= =

1、【N个全不同的球放入K个全不同的盒子 ——无限制】

每个球都有k种选择方案，所以根据乘法原理，方案数就是k^n。

2、【N个全不同的球放入K个全不同的盒子——每盒至多1球（n<=k）】

盒子：□□□□□□□□□□□□□□□□□□

球：●●●●●●

从盒子集合里面有序地取出k个盒子（一共有P(k,n)种方案），将球依次放入。

所以一共是P(k,n)种方案。

3、【N个全不同的球放入K个全不同的盒子——每盒至少1球（n>=k）】

盒子：□□□□□□□

球：●●●●●●●●●●●●●●●●●●

先简化为第二类stirling：

#n个元素划分k个集合，每个集合至少一数#

即

#将n个不同的小球全部放入k个相同的盒子，要求每个盒子都不为空。#

该问题的解S(n,k)=S(n-1,k-1)+k*S(n-1,k);(S(n,n)=1,S(n,1)=1)

然后考虑盒子有顺序，即乘上k的全排列的方案数k!

所以最终问题的解为k!S(n,k)。

4、【N个全同的球放入K个全不同的盒子 ——无限制】

该问题可以转化为：

有k类元素，每类可以取无限个，总共取n个数，有多少种方案

{●|●|●●●|●●|●●●●|●|●|}

可以看出，就是在一串球里面放k-1个栅栏所得的方案数，可以放栅栏的总位置为n-1个，得出为C(n-1,k-1)。

{●|   |●●●|●●|●●●●|●|  |}

因为无限制，即有可能为空（图见上），所以n很可能会小于k，所以这时候C(n-1,k-1)就不合法了。

接下来想到一个办法，设每两个栅栏之间早就有一个球了，于是示意图变成了：

{●[●]|[●]|●●●[●]|●●[●]|●●●●[●]|●[●]|[●]|}
注：[●]为想象中多加进去的球

这样一来和加球之前方案数一定一样。

所以总方案数=C(n-1+k,k-1)=C(n+k-1,k-1)=C(n+k-1,n)。

5、【N个全同的球放入K个全不同的盒子 ——每盒至多一球(n<=k)】
盒子：□□□□□□□□□□□□□□□□□□□□□
球：●●●●●●●●●●●
从k个盒子里无序取出n个盒子然后依次放入n个球，方案数为C(k,n)。

6、【N个全同的球放入K个全不同的盒子 ——每盒至少一球(n>=k)】
该问题与4号问题有异曲同工之妙，因为无限制的隐含条件即为每盒至少0个球，现在变成了每盒至少1个球。

参照4号问题里面首先列举的放k-1个栅栏，共有n-1个放栅栏的位置，所以总方案数=C(n-1,k-1)。

7、【N个全不同的球放入K个全同的盒子 ——无限制】

在3号问题里面已经介绍了第二类stirling数S(n,k)，即n个元素划分k个集合，每个集合至少一数。

假设把球全部放入一个盒子里，方案为S(n,1)，然后把球全部放入两个盒子里，方案为S(n,2)……把球全部放入k个盒子里，方案为S(n,k)

该问题方案总数即为∑S(n,i)。

8、【N个全不同的球放入K个全同的盒子 ——每盒至多一球(n<=k)】
仅有1种方案。

9、【N个全不同的球放入K个全同的盒子 ——每盒至少一球(n>=k)】
解即为第二类stirling数S(n,k)。

10、【N个全同的球放入K个全同的盒子 ——无限制】
解为p(n,k)=p(n-1,k-1)+p(n-k,k)。
球：{●|●●●|●●●●●|●●●|●●●●●|●●●●}
因为盒子全部相同没有顺序，可以将其按照内容多少排序得到
球：{●|●●●|●●●|●●●●|●●●●●|●●●●●}
p(n-1,k-1)即考虑将现在的第n个球单独放进一个盒子里面。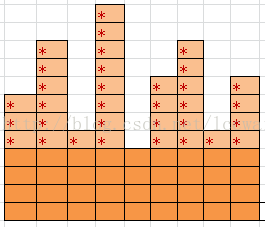

该柱状图高度表示该位置目前放了多少个小球，可以看出，因为方块相同，所以不论怎么变换组合，都不与下面四行有关