经典光流算法Lucas-Kanade（有图助理解）

前言

光流法是计算机视觉领域非常常用的算法，深度学习时代的CV工程师可能会用到光流法，但鲜有对其实现原理做深度地探索的。今天正好趁着复现一个项目把LK光流法的算法进行一个探索和整理。

先看一个LK光流法实现的效果：代码可戳《python光流实验》

---

1. 问题建模

光流法是通过比较连续两帧的差异来估计运动物体移动的。
咱们先选定一个点$p$，在理论上，时间$t_0$时刻，经历过$\Delta t$后，点$p$会移动到另一个位置$p^{\prime }$，并且$p^{\prime }$本身和周围都有着与$p$相似的亮度值。朴素的LK光流法是直接用灰度值代替RGB作为亮度。
根据上面的描述，对于点$p$而言，假设$p$的坐标值是$(x,y)$，有
$$I(x,y,t)=I(x+\Delta x,y+\Delta y,t+\Delta t)$$ $(公式1)$
其中，$I(x,y,t)$代表点$p$在时间$t$时刻的亮度值（灰度值）。经过了时间$\Delta t$以后，点$p$分别向两个轴移动了$\Delta x$、$\Delta y$的距离。
根据泰勒公式：（咱们在这里把$x$、$y$看做是$t$的函数，把公式(1)看做单变量$t$的等式，只需对t进行展开）
$$I(x,y,t)=I(x,y,t)+\frac{\partial I}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial I}{\partial y}\frac{\partial y}{\partial t}+\frac{\partial I}{\partial t}+o(\Delta t)$$$(公式2)$
最后那一项是佩亚诺余项，更高阶，咱们可以假定为0。所以，根据公式2，我们可以得到：
$$\frac{\partial I}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial I}{\partial y}\frac{\partial y}{\partial t}+\frac{\partial I}{\partial t}=0$$$(公式3)$
设$$\frac{\partial x}{\partial t}=u,\frac{\partial y}{\partial t}=v$$
$$\frac{\partial I}{\partial x}=I_x,\frac{\partial I}{\partial y}=I_y,\frac{\partial I}{\partial t}=I_t$$
则公式(3)可以简写成：
$$I_{x}u+I_{y}v+I_t=0$$$(公式4)$
公式4，便是咱们的核心公式了。其中$u$、$v$代表两个方向(x方向和y方向)的移动速度，$I_x$、$I_y$、$I_t$代表了亮度在三个轴上的偏导（也就是梯度）。把$u$、$v$计算出来，咱们的光流也就算出来了。
拿到当前帧，假设我们要计算点$p$的光流。其中$I_x$、$I_y$都可以通过当前帧计算出来，而$I_t$可以通过两帧的差分计算出来。所以，对于公式(4)而言，未知数只有$u$和$v$。

2.Lucas-Kanade

LK算法就是用来求解公式(4)的。LK有一个window的概念，即我先划定一块区域比如(5x5)的像素区域，我们可以认为这块区域每个点的移动速度$u$、$v$是一致的。
首先，$I_x$、$I_y$是怎么得到的呢？对于光流法，咱们有个理想的假定就是：运动物体只会做平移。所以，亮度梯度咱们只需考虑当前帧的梯度即可。对于$I_t$我们在两帧做一个差分就可以得到。

咱们看当前帧，也就是右边那个。$I_x(3,3)=0$是因为在$x$轴的数值左右都是3，没有梯度变化。$I_y(3,3)=1$是因为在$y$轴数值变化幅度为1。上图显示的情况，咱们只能算出y轴速度$v$，没有办法算出水平（x轴）速度$u$。这是因为该移动目标本身在x轴方向上就没有亮度变化。这也是一种典型的问题，叫孔径问题(Aperture Problem)。
孔径问题是讲，如果我们通过一个小孔来看全局，很多情况下的移动信息我们是看不出来的，这个用一张图就可以很好理解：

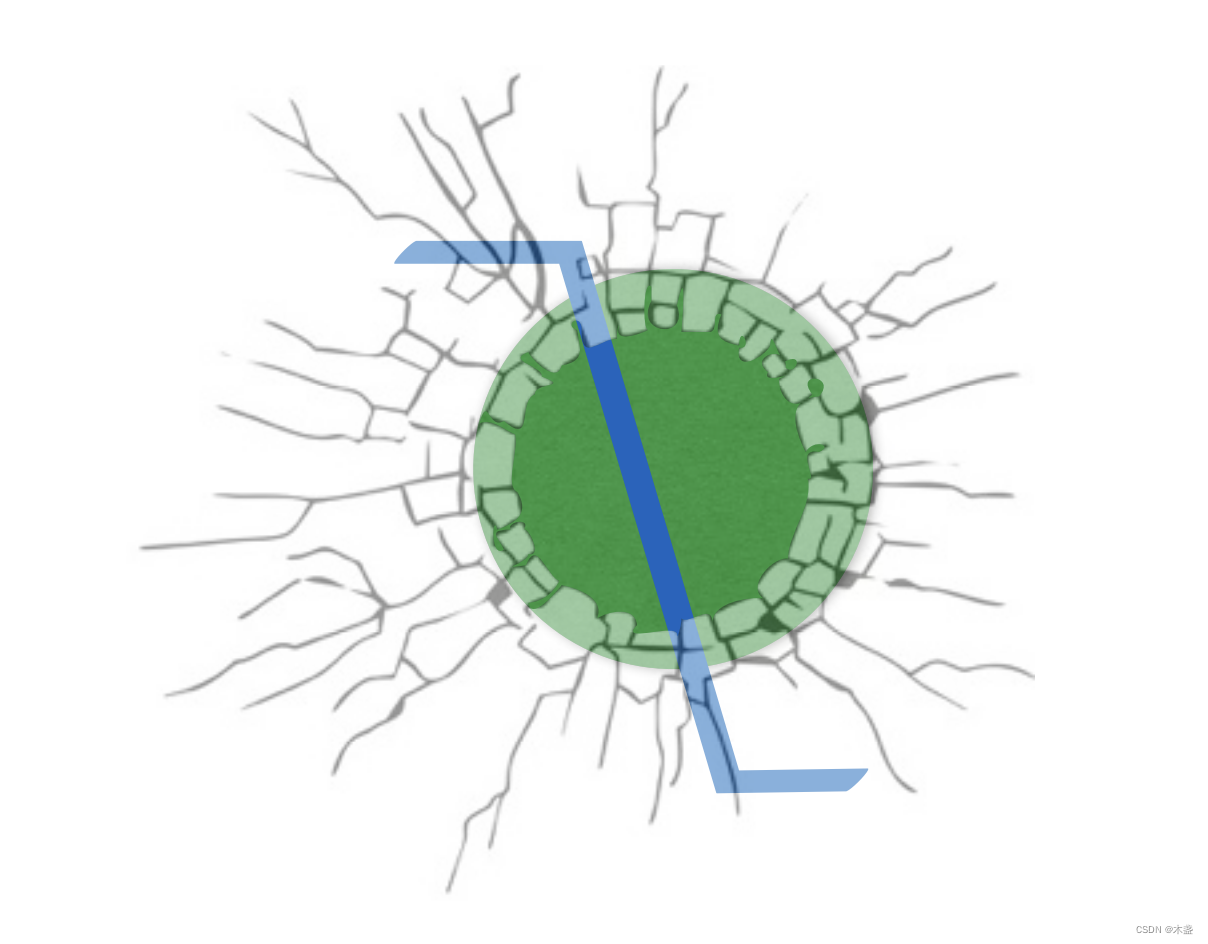
假设墙上破了一个洞，咱们通过这个洞来看一个图形的移动情况。假设，我们看到的是上图这种情况，绿色部分就是我们的视野，我们无法判断这个图形是否是沿着切线方向移动或者是静止。听懂掌声。
那么基于小区域的LK光流法也可能遇到Aperture Problem，所以我们在追光流的时候，选点通常会选目标的角点(corner)。角点的情况如下图：

如果角点在视野内的话，咱们就可以判断这个图形的运动方向。听懂继续掌声。
接着公式(4)，咱们如果通过window方式求解$u$、$v$，那还是很好办的。假设咱们取的是5x5的window，那么window内的每个点，我们都认为有一样的移动方向，咱们可以构建出25个等式。求解二元一次方程，通常两个等式就可以求解。但那是理想情况，实际情况是没有一组$(u,v)$能同时满足这25个等式，咱们要做的是最小化这个差异。

写成矩阵形式：

只需找到一组$(u,v)$，即上图中的$x$，满足
$$\hat{x}=\underset{x}{\mathrm{argmin}}||\mathbf{A}x-b|{|}^2$$$公式(5)$
这里就可以用最小二乘法来进行优化了，分别求偏导得出导数为0的点的值就是最优值。可推导出，

这便是Lucas-Kanade光流算法的公式了。

参考：http://www.cs.cmu.edu/~16385/s15/lectures/Lecture21.pdf