线性代数的本质（九）——特征向量与特征值

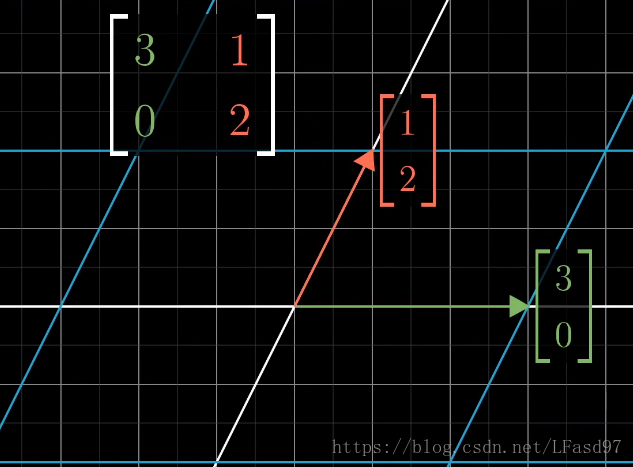
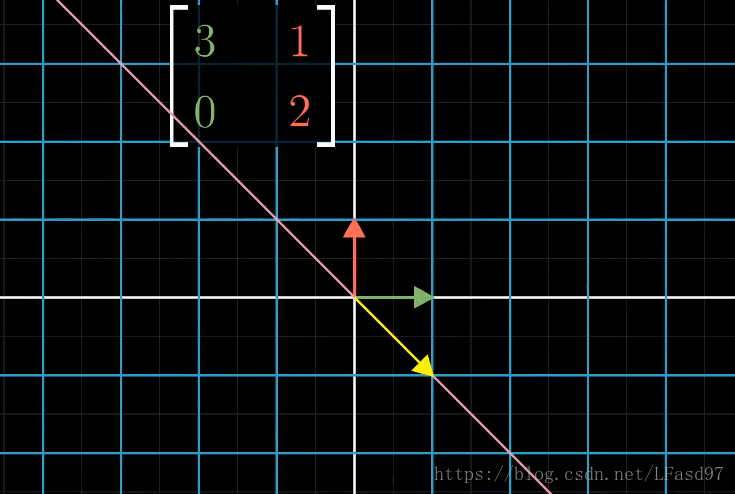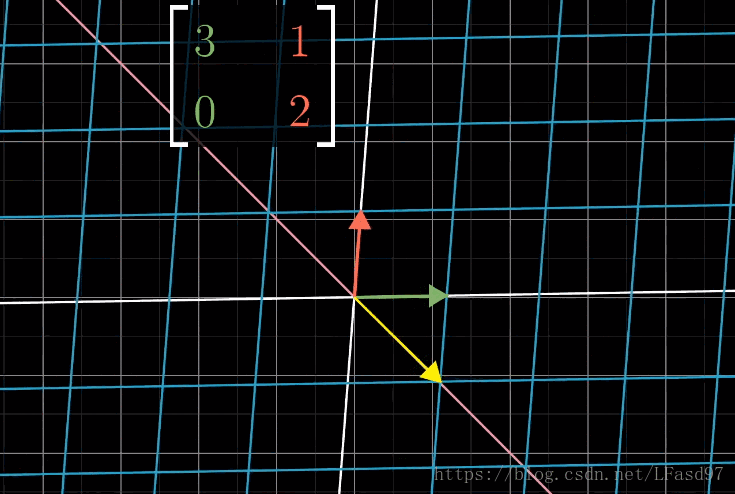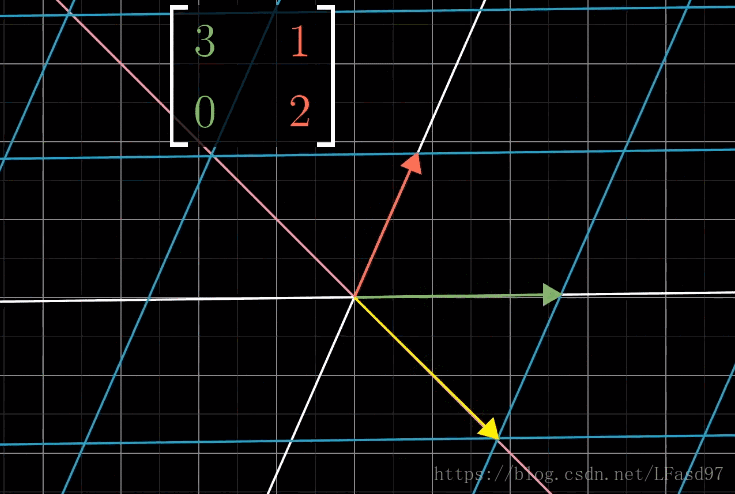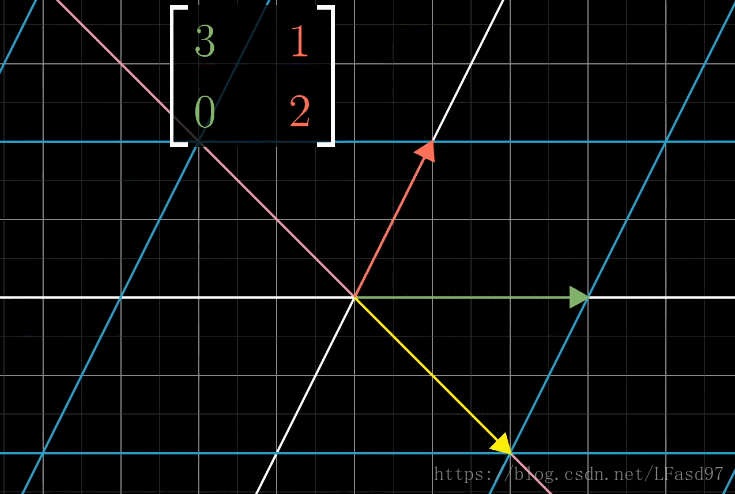
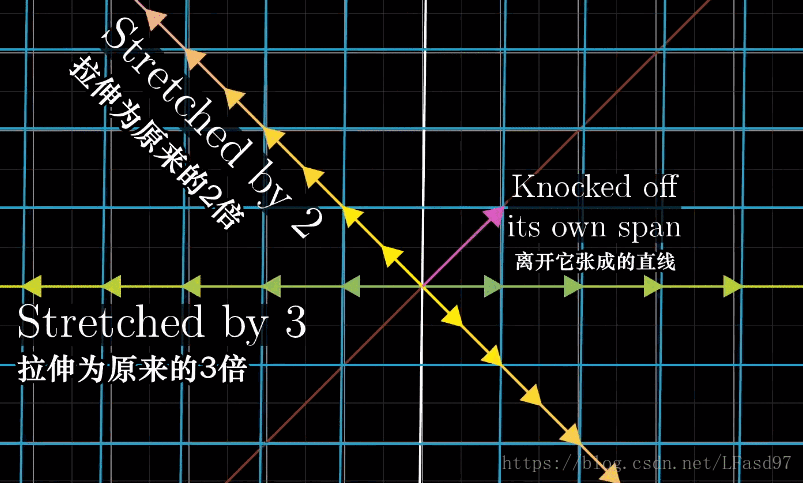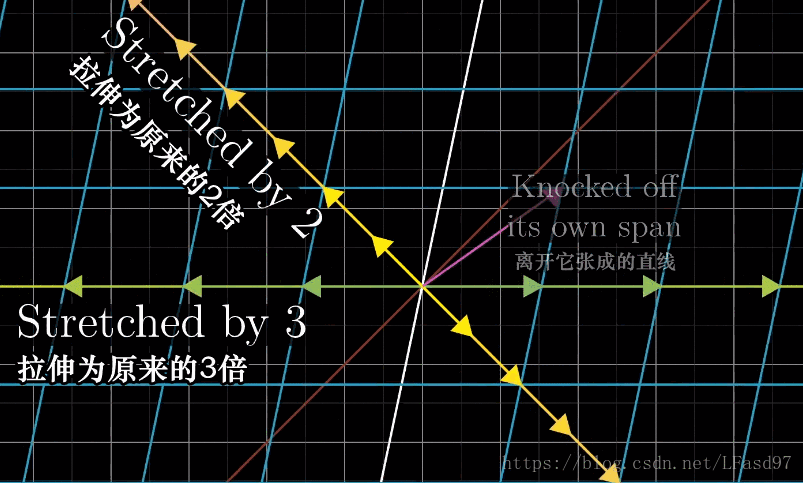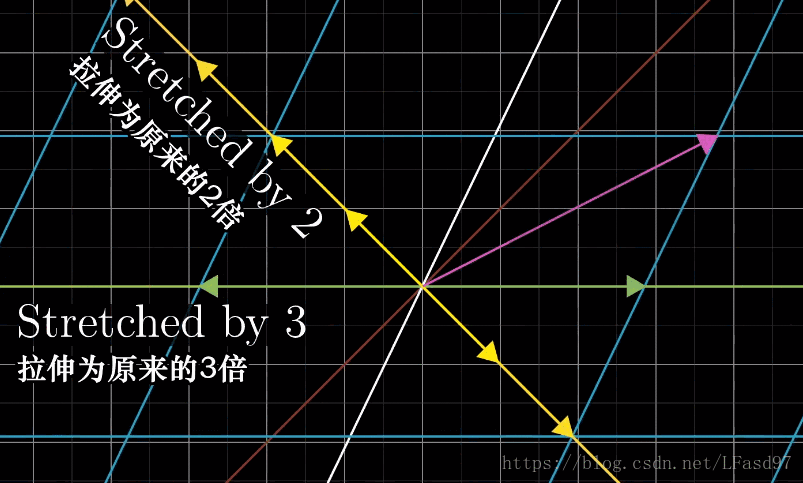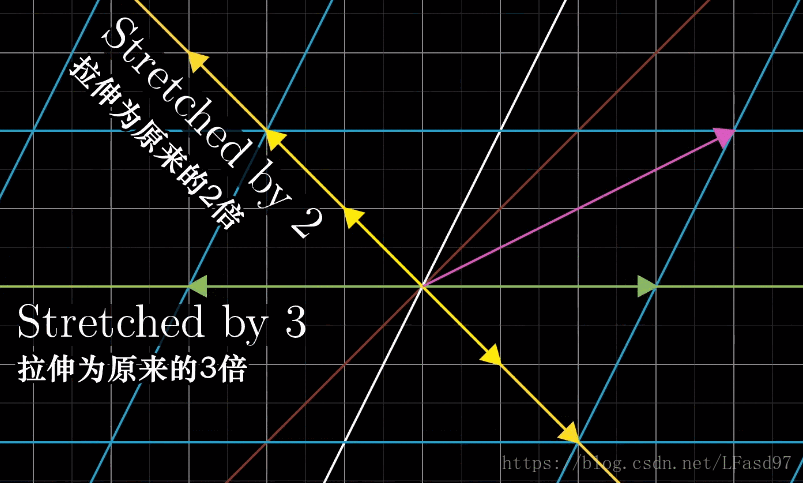
首先让我们来考虑下面这个变换

我们关注这个变换对一个特定向量的作用

可以看出，这个变换使向量脱离了它本身张成的空间（一条直线），除了这个向量以外，这个二维向量空间中的绝大部分向量在变换后也会脱离它原来张成的空间。不过对于这个变换来说，仍然有一些特殊的向量会留在向量本身张成的空间中，这个变换只是对这些特殊的向量进行了缩放而已。

这个 $\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$ 矩阵一共有两类能够保持在原来张成空间的向量。

看到这里，你们应该能猜到了，这些特殊的向量就是这个变换的特征向量，每一个特征向量都有一个被缩放的比例，就是特征值。

再了解了上面的概念后，我们再来看看矩阵特征向量和特征值的公式，$A$ 表示一个变换，$\lambda$ 表示一个系数

$A\vec{v}=\lambda \vec{v}$

这个公式说了左边矩阵向量乘积等于右边向量数乘，就是上面动画中表现出来的。我们来看看具体的计算过程

$A\vec{v}=\lambda \vec{v}$

把右边也换成矩阵向量乘法，在右边添加一个单位矩阵 $I$

$$\begin{gathered} A\vec{v}=\lambda I\vec{v} \\ A\vec{v}-\lambda I\vec{v}=0 \\ (A-\lambda I)\vec{v}=0 \end{gathered}$$

最后我们可以得出，$A-\lambda I$ 代表的变换将空间压缩到了更小的维度，即 $\det (A-\lambda I)=0$，因为只有在 $A-\lambda I$ 将空间压缩到更低维数的情况下，才会存在一个非零向量在变换后变成零向量。所以，现在我们只要能够求出满足 $\det (A-\lambda I)=0$ 的特征值 $\lambda$ ，然后根据 $(A-\lambda I)\vec{v}=0$ 算出具体的特征向量 $\vec{v}$，以 $A=\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$ 为例。

$$\begin{gathered} \det (\left[\begin{array}{cc}3-\lambda & 1\\ 0& 2-\lambda \end{array}\right])=0 \\ (3-\lambda )(2-\lambda )=0 \end{gathered}$$

解得 ${\lambda }_1=2$ ${\lambda }_2=3$

接下来我们把求解出来的 ${\lambda }_1$ 和 ${\lambda }_2$ 分别代入 $(A-\lambda I)\vec{v}=0$ 中，接下来我们可以根据零空间得出 $\vec{v}$ 的解了。

如果一个矩阵的特征向量就是基向量会是怎样的。满足这样的的矩阵只有对角矩阵，即矩阵除了对角元素以外其他元素都为0，$\left[\begin{array}{ccc}x& 0& 0\\ 0& y& 0\\ 0& 0& z\end{array}\right]$，我们解读对角矩阵的方法可以是——每一个基向量都是特征向量，矩阵的对角元素是对应基向量的特征值。我们计算对角矩阵的乘积是非常好算的，${\left[\begin{array}{cc}3& 0\\ 0& 2\end{array}\right]}^{100}=\left[\begin{array}{cc}{3}^{100}& 0\\ 0& 2^{100}\end{array}\right]$，而计算 ${\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]}^{100}$ 却不是那么简单了。

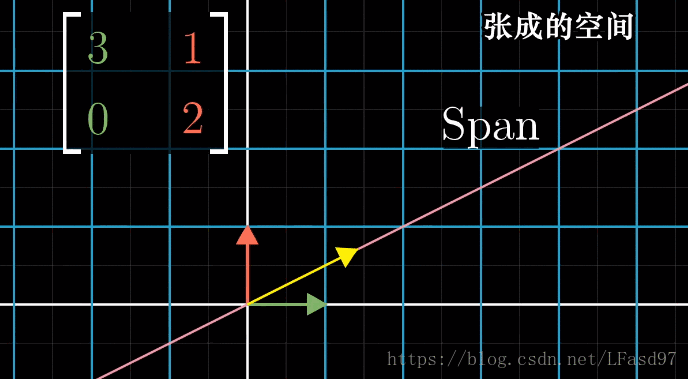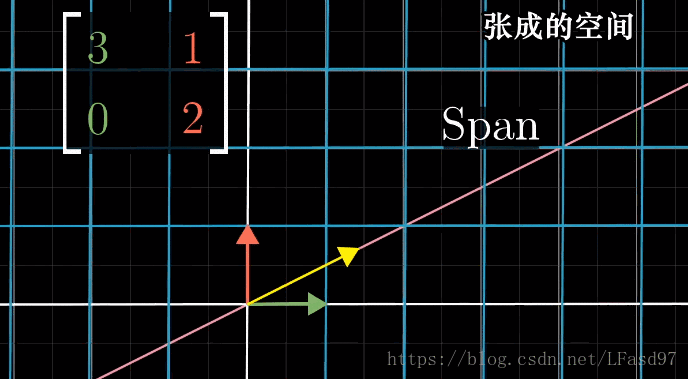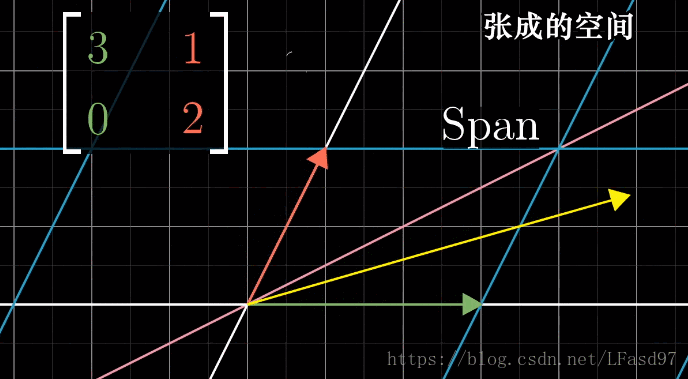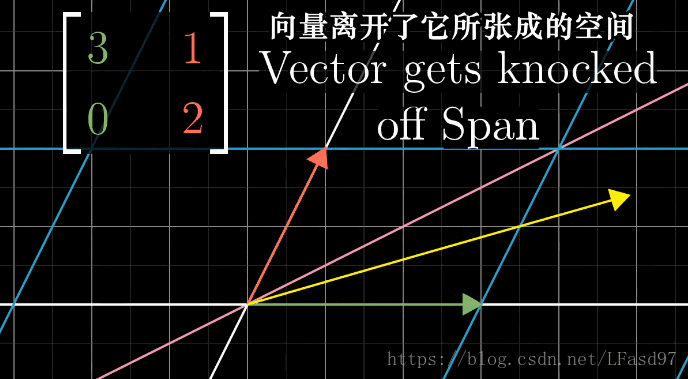
像对角矩阵这种基向量就是矩阵特征向量的特殊矩阵并不多见，那我们如何计算那些基向量不全是特征向量的矩阵呢。我们知道线性无关的向量可以作为基向量，例如在二维空间中 $\left[\begin{array}{c}1\\ 1\end{array}\right]$ 和 $\left[\begin{array}{c}1\\ -1\end{array}\right]$ 这两个向量可以张成整个二维空间，现在回想一下上一节的基变换，如果一个矩阵的特征向量可以张成全空间，那我们可以使用基变换变换我们的坐标系使得这些特征向量就是基向量，这样就满足了基向量就是特征向量的条件。例如上面 $\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$ 的特征向量 $\left[\begin{array}{c}1\\ 0\end{array}\right]$ 和 $\left[\begin{array}{c}-1\\ 1\end{array}\right]$ 可以张成全空间，所以新的坐标系为 $\left[\begin{array}{cc}1& -1\\ 0& 1\end{array}\right]$，接下来我们用新坐标系来描述原始坐标系的矩阵 $\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$，这里就要用到上一节讲到的相似矩阵了 ${\left[\begin{array}{cc}1& -1\\ 0& 1\end{array}\right]}^{-1}\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]\left[\begin{array}{cc}1& -1\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}3& 0\\ 0& 2\end{array}\right]$

然后我们在心坐标系中计算矩阵 ${\left[\begin{array}{cc}3& 0\\ 0& 2\end{array}\right]}^{100}$ 然后转换成原始坐标系，其结果等于直接在原始坐标系计算 ${\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]}^{100}$，$\left[\begin{array}{cc}1& -1\\ 0& 1\end{array}\right]{\left[\begin{array}{cc}3& 0\\ 0& 2\end{array}\right]}^{100}{\left[\begin{array}{cc}1& -1\\ 0& 1\end{array}\right]}^{-1}={\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]}^{100}$ 最后就通过简单的方式完成了计算，当然这种方法只能用在矩阵的特征向量能够张成全空间这个大前提下。