可视化信息理论(Visual Information Theory) （中）

点击阅读原文

Codes

编码
我们有可视化概率的方法，现在引入信息理论。
现在假设有一个虚构的朋友Bob，他很喜欢动物并且只说四个单词”dog”,”cat”,”fish”,”bird”。
他搬家到澳大利亚，所以他决定通过二进制来与我交流。所以所有的来自bob的信息就是：

为了交流，我们之间建立起了协议，把单词于二进制数对应起来了：



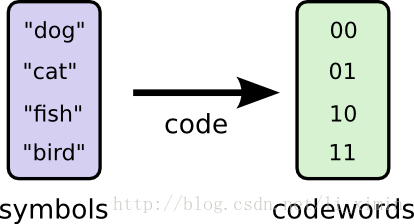
发送信息时，Bob把每个单词替换成对应的二进制数，然后把这些二进制数组合在一起编码成二进制串：

Variable-Length Codes

很不幸的是，通信服务太贵了，我们决定找到一种方法，降低这个信息发送费用。
发现我的朋友Bob，不会总以相同的频率说这4个动物（单词），他最喜欢狗，说狗的频率会很高，而狗又喜欢追猫，所以说猫的频率次之，再其次就是其它两种动物，那么我们可以假设动物被提及的概率分布：

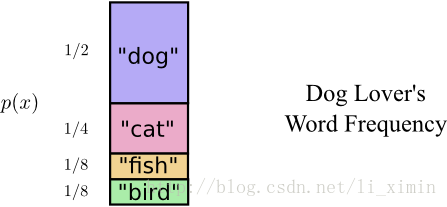
我们会意识到，老的编码方法总是以2个位数字在传送信息，忽略了单词提取的频率（概率）。
有一种很好的方法来可视化这个情况，在下面的图片中，我们用竖线来表示每个单词出现的概率, $p(x)$，而水平线用来代表对应编码的长度， $L(x)$。注意发送一个单词我们平均都要用2个bits（即下图着色矩形的面积）：



可以发现，用一种可变长的编码方式可以减少编码的平均长度（把使用最频繁的单词编成更短的编码）。当我们把一些单词编码变短时，就意味着需要把其他单词的编码变长。为了降低信息的长度，理想状态下是把所有的字符编码都变短，但我们特别需要把最通用的一些变短。所以我们用下面这个编码方法，让字符编码更短：



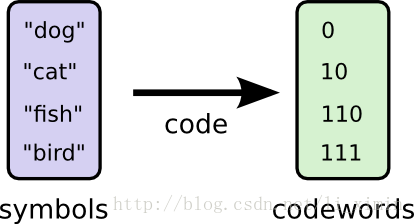
让我们再次把它可视化。注意到使用最频繁的关键字编码更多了而其它的变长了。这个结果按净计算，会用更少的编码。即原文编码的期望值更小了，现在是1.75 bits:



（为什么不用1来编码一个关键字呢？不幸的是，这样的编码会让信息产生歧义，我们稍后讲解）
这样的编码方式是最好的方法了，没有其它方法的编码期望会比1.75更少。
这是一个很简单的基本界限，说话的信息，发生的事件，都需要平均至少1.75bits来交流，无论我们的编码方式如何特别，都不可能让信息编码的平均长度比1.75更少，这种界限我们称为分布的熵(the entropy of the distribution)。



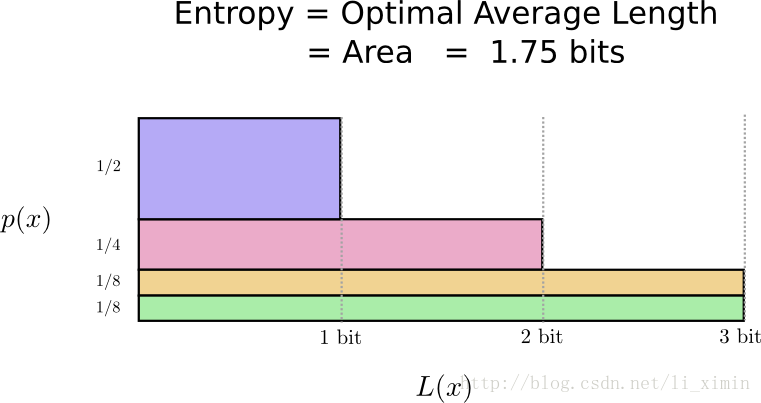
想要理解这样的概念，我们需要了解的关键是让一些编码更短，而让另外一些编码更长。一旦我们理解了这些，我们就会知道最好的编码方式是怎样的。

The Space of Codewords

如果有一个bit，那么就有2种编码，如果有2个bit，则有4个编码方式，如果有n个bit，则有$2^n$种编码：

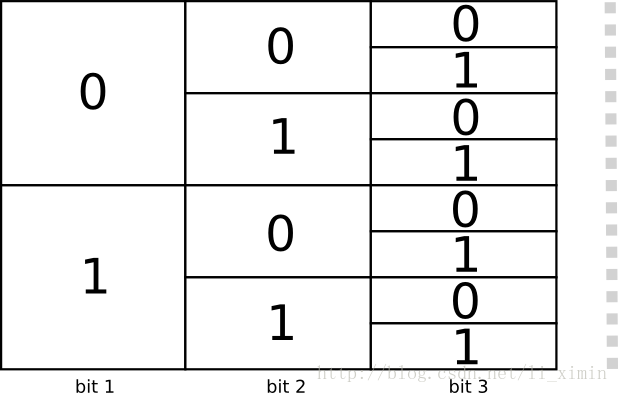
如果是可变长的编码方式呢（即有一些原文的编码会比其他的编码长）？每个原文的编码长度都不一样的情况下，我们如何来确定用多少字节来编码这些原文呢？
我们回到Bob的问题，把他的原文编码后连接成编码串：



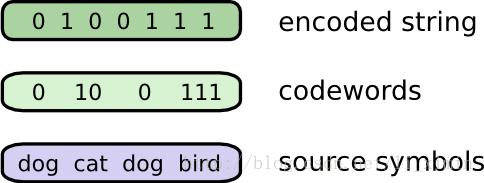
我们如何把一个编码串分割成一个一个对应的密文呢？当这些密文的长度都一致的时候是很简单，把他们挨着挨着平均分割就好了。但是每一个原文的密文长度都一样时，我们需要如何做呢？
对于密文串，我们肯定要保证它是唯一的，可解的，不是模棱两可。如果对每一个密文都有特定的起始或者结束标识符，这也是一种方法，但会加大信息的冗余。如果只传送0和1，有没有方法保证密文的唯一性呢？
在编码时，对于可变长度的密文很有可能解码成不同的信息，比如0和01都代表了不同的信息，当遇到密文串0100111 时，就会解码成不同的信息了。由此可以看出我们需要的编码规则是如果看到了一个密文，那么再往后出现的编码不能与之前的密文组成其它的密文，也就是说一个密文的内容不能是其它更长密文的前缀。这条性质称为前缀性质( prefix property)，满足这条性质的编码则称为前缀编码(prefix codes)。
对于这种性质，一种有效的编码方式是每一个密文都会让更长的密文做出牺牲，如果短密文已经确定，那么比它长的所有密文都不得以这个短密文开头。比如我们使用0成为了一个密文。任何以0开头的密文都不能再使用，如01,001,010100等等，因为使用后密文就缺失了唯一性。



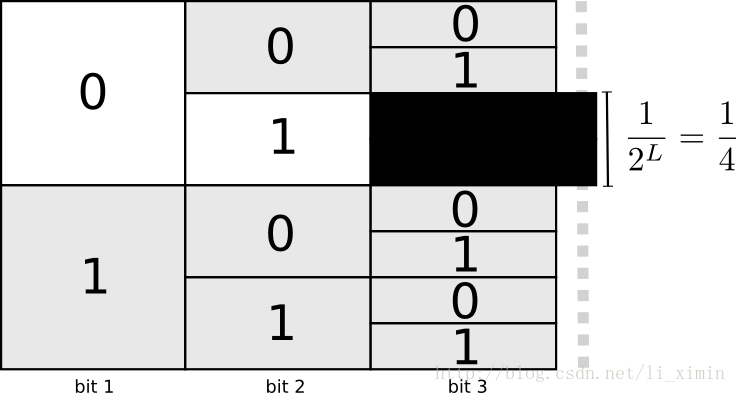
如上图，如果有密文以01开始，那么后面1/4的密文就不能够再使用。这就是要使用2bit密文的代价，为了编码更多的密文，有一些密文就得增长。对于不同长度的密文，总会有这种情况产生，一个短的密文就会牺牲更多可能表示密文的空间，就会让其它密文变得更长。我们需要正确的权衡产生的影响。

Optimal Encodings

可以理解为简短编码的长度是有一个限定的度量在里面，每减短一个bit的密文就会牺牲一些编码的可能性从而让其它密文的长度增长。
如果要用一个0长度的密文来编码，那么代价就是100%密文空间，即如果要用一个0长度的密文，就不能用其它密文来进行编码了。如果要用长度为1bit来做密文，那么代价牺牲了50%的密文空间，即如果选用0或者1来做密文，那么以0或1开始的密文空间都应该作废，所有会牺牲掉50%的密文空间，依次类推。总体上，牺牲的密文空间是随着密文长度成指数趋势下降的：

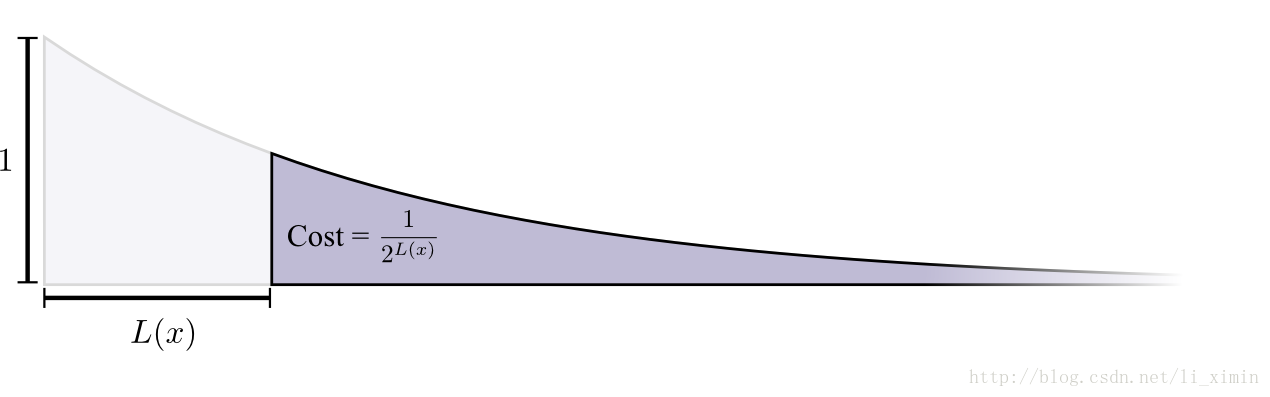
如果代价是以指数衰减，那么这个高度和面积也是成指数衰减。
我们想要减少密文的长度，目的是减少信息的期望长度，密文的期望长度是密文出现的概率乘以密文的长度。假设我们有一个4bit的密文，出现概率是50%，那么我们的期望就是4*50%=2bit。我们做图来表示：



以上两者数据（代价和期望长度）都跟信息的长度有关，信息的长度决定了整体信息的平均长度。我们可以把这两者画在一张图下：



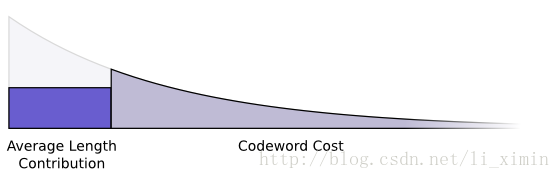
更短的密文减少整体信息的平均长度，但是代价比较大，较长的密文增加了信息的长度，但是代价更小。

什么样的方法才能最好的找到两者之间的平衡？对于一些信息，我们到底应该用多长的密文来表示呢?
就像应该在平时用得更多的工具上投入更多一样，我们需要在使用更频繁的密文上下功夫。这里就有一种方法：更加密文使用的频繁程度来调整密文的代价。比如一个密文有50%的概率要使用，那么我们可以花50%的密文空间来让这个密文简短一些。如果这个密文只有1%的概率用到，那么只花1%的代价来表示这个密文。这个方法是比较简单的，并且这个就是最佳的方法（ 证明过程请阅读原文）