可视化信息论(2015年10月14日)

这里是原文
我热爱用一种新的方式去思考世界。我尤其热爱当有一些模糊的想法形式化成某些具体的概念。信息论就是一个非常好的例子。
信息论给了我们一个具体的语言来描述很多事情，我是多么的善变？知道问题A的答案对于知道问题B的答案有什么帮助？一些想法和另一些想法有多么的相似？当我还是小孩的时候，我就有一些关于这些问题的粗略想法，但是信息论把这些问题抽象成具体的，强大的概念。不管是从数据压缩，量子物理还是机器学习，以及其他很多和这三者有关的领域，信息论的概念都有着大量多样的应用。
不幸的是信息论总被认为挺难的，我其实不是很理解，可能是有些书写的太糟糕了，事实上，它完全可以用可视化的方法简单的说清楚。

可视化概率分布

在我们深入到信息论之前，让我们先想一下如何可视化一个简单的概率分布。这在之后会有用，我们也能在这里方便的解释它。这些可视化概率的技巧不仅在理解概率本身而且在其它应用上都会非常有用。
我住在California。有时候会下雨，但大部分时候是出太阳的。我们假设它有75%的时间是下雨的，这可以这样可视化的表达：

大部分的时间我是穿T恤的，但有时候我也会穿外套。假如我们有38%的时间在穿外套，图片的表述也很简单。

那么我们怎么同时可视化这两件事情呢？如果这两个事件不相交的话，也就是说它们是独立的话，这是一件简单的事情。比如我今天穿不穿T恤确实不影响下周的天气。这样我们可以一个维度画一个变量得到以下的图：

注意到水平和垂直方向上都是直线，这就是两个独立事件图形表示的特点。我今天是否穿外套的概率不会随着未来一周天气的变化而变化。也就是下周下雨且我在今天穿外套的概率就等于我在今天穿外套的概率乘以下周下雨的概率。它们不相交。
当两个事件相交，对于某些对变量来说就会增加额外的概率，而某些对变量来说就会减少概率。比如，我穿外套且下雨这个事件就会增加额外的概率，因为这两个变量是相关的，它们使得各自都变得更加有可能发生。我在下雨天穿外套的概率比在一个不知道下不下雨的天气里面穿外套的概率要大。
可视化的表示就是有些方块变得膨胀了，而另外一些方块因为两件具体的事情同时发生的概率比较低，变得收缩了。

这看起来还不错的，但是这其实对于理解问题的关键帮助还是不大。下面，我们只考虑一个变量，比如说天气。我们知道下雨或出太阳的概率大概有多大。对于这两个具体的事件我们再去考察条件概率。如果是晴天我有多大可能穿T恤？我在下雨天穿外套的概率又有多大？

有25%的概率会下雨，如果下雨，我有75%的概率会穿外套。所以我穿外套而且天气在下雨的概率是25%乘以75%，大概是19%。

$$p(rain, coat)=p(rain)\times p(coat \ |\ rain)$$
这是概率论中一个基本等式的应用。
$$p(x, y)=p(x)\times p(y \ |\ x)$$
我们分解了这个分布，将它分解成两个分布的乘积。首先我们看某个变量，比如天气，分布的一个特定的值。然后再看另一个变量，我的衣着，也就是给定第一个变量条件下的分布。
其实选择哪个变量来开始是随意的。我们可以从我的衣着开始，然后以这个为条件来考虑天气。这看起来可能不是很直观，因为我们知道只有天气影响衣着有因果关系，反之没有。但这样同样是对的。
让我们看一个例子，随便选一天，有38%的概率我会穿外套。如果我知道我穿了外套，有多大可能是雨天呢？我在下雨天穿外套的可能性比较大，但是加州下雨的可能性又不是很大，所以说50%的可能是下雨的也是说的通的。这样的话，我穿外套且下雨的概率就是38%乘以50%大概是19%。
$$p(rain, coat) = p(coat)\times p(rain\ | \ coat)$$
这给了我们另外一个可视化同一个分布的图。

我们注意到，标签上和上一副图有不同的意义。现在T恤和外套是边缘概率。另一方面，有两组下雨和出太阳的标签，各自是对应在我穿外套和我穿T恤条件下的情况。(你可能听说过贝叶斯分布，你可以放在一起看看这两种不同看待概率的不同角度。)

题外话：辛普森悖论

这些可视化概率分布的方法真的有用吗？我认为有用的。在没有用来解释信息论之前，看上去用处还不太大，这里我们先用这种方法来解释一下辛普森悖论，看看这种方法的作用。辛普森悖论是一个非常unintutitive的统计情景。在直觉上，真的是很难理解。Michel Nielsen给出了一个挺漂亮的解释，Reinventing Explanation，我打算用我的方法来试试做自己的解释。
要测试两种治疗肾结石的方案。一半的人用方案A，而另一半用方案B。用方案B的人好像存活率高于方案A。

然而，有小肾结石的病人用方案A的存活率高于用方案B。而且有大肾结石的病人用方案A的存活率也要高。怎么会这样呢？
问题的关键是这个研究没有足够的随机化。用方案A的病人倾向于有大肾结石，而用方案B的病人倾向于有小肾结石。从结果上看有小肾结石的病人本身更加容易存活。

为了更好的理解它，结合之前的两个图，我们得到一个三维的图。

从图中我们可以看出不管是对于小肾结石的病人还是大肾结石的病人，方案A都要优于方案B。方案B之所以看起来优秀，因为它应用的病人更加容易存活。

编码

好了现在有了可视化信息论的方法，我们可以看看信息论了。从我们的一个想象的朋友Bob开始。Bob十分喜欢动物，它经常说动物的事情。事实上，它一直只说4个词，“dog”，“cat”，“fish”和“bird”。
在我的虚构下，几个礼拜前，Bob搬到了澳大利亚。而且，这个sb决定只用二进制进行通信。所有从Bob那边传过来的信息都是这个样子的：

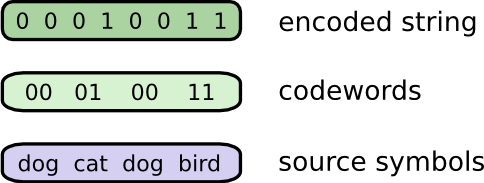
我要和Bob进行通讯的话，必须要进行编码，这样才能将词映射成二进制码。

要发送信息，Bob将每个词用对应的二进制码代替，然后连接起来形成编码字符串。

可变长编码

不幸的事情是，在虚构的澳大利亚通信的费用非常昂贵。从Bob那里接收每一位，都要花费至少5美元。而且我有说过，Bob很唠叨吗？为了不让自己破产，Bob和我决定好好研究研究是否存在什么方法让我们平均的通讯成本尽可能的低。
因为Bob说每一词的频率是不一样的。Bob喜欢狗，所以他说狗的概率是最大的。有时候，他也会说说其它动物，比如老是和他的狗打闹的猫。下面是他的词频图：

看起来我们抓住了问题的关键。之前不管我们用词汇的频率是怎么样的，我们给每个词汇都分配两位。
如果用可视化的方法来表示这个方法看上去可能会直观一点。在下图中，我们用垂直的轴来表示每一个词的概率$p(x)$，用水平轴来表示对应的编码长度，$L(x)$。在这里我们平均发送一个词的成本是2位。

也许我们足够聪明，可以找到一种编码方式，使得概率最高的词汇有非常短的编码。对我们的挑战主要是编码之间存在竞争关系——使得某些编码变短，意味着有些编码要变长。要最小化平均的成本，理想上我们希望所有的编码都尽可能的短，但是我们尤其希望最常用的词有短的编码。所以最后得到的编码使得常用的词（“dog”）有相对短的编码，而不常用的词(“bird”)有相对长的编码。

从另一个角度再来看一下这种编码方式。最常用的词有最短的编码，而不常用的词有较长的编码。最后的结果是我们得到了更少的区域。也就是得到了每个词更短的期望编码长度。现在这个数字是1.75位了。

（你也许想知道：为什么不用1去作为一个编码，可惜的是，这样做会得到一个在解码时不明确的编码字符串。我们会在接下去继续讨论这个问题。）
告诉你一个事实，上面的这种方式其实是最优的编码方式。也就是对于这个分布，$p(x)$，没有其它的编码方式可以得到小于1.75的期望编码长度。无论我们多么的聪明，我们都不能找到更好的了。我们把这个基本的约束叫做分布的熵——我们会马上详细的讨论它。

要理解这个约束的关键是理解要使得某些编码变短会使得另一些编码变长。一旦我们理解了这一点，我们就能大致想象最佳的编码方式了。

编码空间

1位的编码有2个编码：0和1。2位的编码有4个编码：00，01，10和11。每增加1位，可能的编码就会翻番。

我们关心的是变长的编码，也就是有些编码长，有些编码短。我们可能会有简单的情形，比如在3位编码下有8种编码。我们也可能有更加复杂的情形。比如2个编码用两位，而4个编码用3位。那么怎么确定不同长度的编码到底有几个？
我们回忆一下Bob，通过用词的编码连接起来，他把消息映射到编码字符串。

有一个关键的问题我们要考虑的就是，当我们选用一个编码方案，我们还要考虑它是否能够唯一的解码。当每个编码是一样长的时候很简单——只要按步长分割编码字符串就可以了。但是由于编码的长度不相同，解码的时候就需要关注编码的内容了。
我们要求解码结果的唯一性。如果我们在每一个编码后面放一个终止编码，这个问题就又变得简单了。但是我们不放，我们只发送0和1，我们要从编码字符串本身来解码。
很有可能我们得到的编码不能唯一的解码。比如想象一下，0和01是两种编码。这样的话，编码字符串0100111的第一个编码是什么就变得不确定了。我们要得到的特性是，如果我们看到一个特定的编码，不应该还有一个编码是以它为前缀的。这被叫做前缀特性，遵守这种规则的编码叫做前缀编码。
一种有用的理解方式是，获得每一个编码就需要在编码空间上作出牺牲。如果我们用了编码01，我们就不能用以01为前缀的编码了。因为解码唯一性的要求，我们不能再用010或者011010110了，我们失去了它们。

因为有$\frac{1}{4}$的编码是以01开头的，我们就牺牲了$\frac{1}{4}$的可能编码。这就是我们要获得一个只有两位的编码的花费。也就是这样的牺牲要求某些编码变得更加长。这里面就有不同长度编码之间的权衡。一个短的编码需要牺牲更加大的编码空间，从而阻碍其它编码变短。我们要搞清楚的是，什么是最好的权衡。

最优编码

你可以想象一下你只有有限的预算来获得短的编码。我们要获得一个编码的成本是牺牲掉可能的编码。
要获得一个长度为0的编码的成本是1，也就是所有可能的编码——也就是你要获得一个长度为0的编码，你就不能再有其它编码了。有一个长度是1的编码的成本是$\frac{1}{2}$，比如“0”，这样你就不再可能用那一半以“0”开始的编码了。要获得一个长度为2的编码，比如“01”，的成本是$\frac{1}{4}$，因为有$\frac{1}{4}$的编码以“01”开头。总的来说，成本随着编码长度指数的下降。

我们想要得到短的编码是因为我们想要得到短的平均信息长度。编码的长度乘以概率直接影响平均消息长度。比如我们以50%的概率发送4位的编码，我们的平均消息长度相对不发送这个编码就增加了2位。我们可以画一个长方形。

平均消息长度和成本这两个量通过编码的长度相关。我们的成本决定了编码的长度。编码的长度控制了对平均消息长度的增加量。我们可以把两个量画在一起。

短的编码降低了平均消息长度，但是成本很高。长的编码增加了平均信息长度但是很便宜。

什么是最好的使用有限预算的方法？对于每个词的编码我们应该用多少位？
就像人们更加愿意在经常使用的工具上花费更多的钱一样。有一种自然的预算分配方法是按照和使用频率成正比的方式分配预算。所以有一个词出现的概率是50%，那么就用50%的预算去定义编码长度。如果一个词出现的概率是1%，我们就只用1%的预算，因为我们其实并不是很关心到底这个编码有多长。这是一件很自然的事情，但是这是最优的方式吗？是的，它确实是。下面我将证明它。
下面是问题的可视化的证明，但是我相信需要花费一定的力气才能理解，因为这是本文当中最难的一部分。读者也可以选择跳过这部分，直接进入下一部分。
首先我们画一个具体的例子，我们只用两个词进行通信。词 $a$ 发生的概率是 $p(a)$，词 $b$ 的概率是$p(b)$。我们用上面描述的这种自然的方式分配我们的预算。用$p(a)$的预算为 $a$ 获得一个短的编码，用 $p(b)$ 的预算为 $b$ 获得一个短的编码。

成本(Cost)和长度分布(Length Contribution)重合了。这有什么意义吗？
考虑一下，当我们轻微的改变一下编码长度，成本和长度分布会有什么变化。如果我们轻微的增加编码长度，消息分布长度会随着边界高度成比例的增加，而成本会随着边界高度下降而下降。

所以要使得 $a$ 的编码稍微变短的成本是 $p(a)$ 。同时，我们并不需要每个编码等长，而是需要它随着对应词使用频率的增加而成比例的变短。这个频率对于 $a$ 来说，就是 $p(a)$。所以使得 $a$ 的编码稍微变短获得的收益是 $p(a)$。
有趣的事情是两个导数是相等的。这意味着初始预算有一个有趣的特性，如果你有一点点多的预算，那么你不管是用来使得哪个编码更加短，获得的效果都是一样的。我们真正关心的事情是 $\frac{收益}{成本}$比——这决定了我们会将多余的预算花在哪一个编码上面。在这里面，这个比是 $\frac{p(a)}{p(a)}$，等于1。它独立于$p(a)$——恒定于1。另一个也一样。所以要多投资一点点的话对一任意一个编码效果都是一样的。

对于极小的量来说，其实也不算改变了预算。所以说，上面的论述并没有证明之前的方法是最佳的预算分配方案。要真正证明，我们需要从一个不同的预算方案开始入手，这里我们在 $a$ 上花费更多的预算，相应的在$b$上花费少一些的预算。我们从 $b$ 的预算中拿出 $\epsilon$ 投资到 $a$ 当中。这使得 $a$ 的编码变短，$b$的编码变长。
现在，为 $a$ 购买一个较短的编码的成本是 $p(a) + \epsilon$，为 $b$ 购买一个较短的编码的成本是 $p(b) + \epsilon$。但是收益是不变的。这使得购买 $a$ 的编码的收益成本比是 $\frac{p(a)}{p(a) + \epsilon}$，小于1。另一方面，购买 $b$ 的编码的收益成本比是 $\frac{p(b)}{p(b)-\epsilon}$，大于1。

这时候价格就不再平衡了。投资于 $b$ 的收益要大于投资于 $a$。投资着就会嚷到“买 $b$, 卖 $a$!”。我们这么做了，然后回到了最原始的方案。所有的其它预算方案，都可以通过改进变化到我们最原始的方案。
最原始的方案——随着使用频率成比例的投资于不同的词汇——并不仅仅是自然的方式，而且是最佳的方案。(这里用两个词来证明，但是这很容易扩展到更多的词)。
(仔细的读者可能会发现，我们的最佳预算方案会产生分数长度的编码。这好像是一个问题。这意味着什么？当然，在实践的时候，当你要发送一个编码的时候需要取整。但是我们会看到，当我们发送很多次编码的时候，能够发送分数的编码是有很重要的意义的。所以希望你能耐心的看文章的下一部分。)

计算熵

回忆一下，长度为 $L$ 的编码的成本是 $\frac{1}{2^{L}}$。我们可以通过逆运算来获得给定成本可以得到的编码长度: $\log_2(\frac{1}{cost})$。因为我们在词汇 $x$ 上花费的成本是 $p(x)$ , 所以长度是 $\log_2(\frac{1}{x})$。以下便是各个词的编码长度的最佳选择。

在上一部分里面，我们相当于讨论了给定概率分布 $p$ 通信的平均消息长度的基本约束。这个约束，也就是使用最佳编码方式得到的平均消息长度，被叫做分布 $p$ 的熵， $H(p)$。我们知道了各个编码的最佳长度，我们可以计算熵了。

$$H(p)=\sum_x p(x)\log_2(\frac{1}{p(x)})$$
（人们往往利用恒等式 $\log(\frac{1}{a}) = -\log(a)$将熵写成 $H(p)=-\sum p(x)\log_2(p(x))$，我认为第一种方式更加直接，所以文章将继续使用这种形式。）
不管怎样做，如果我要通信，我就至少要花费这么多的位。
通信需要的平均信息量很明显可以用来压缩数据。它还能用在什么地方呢？是的，它可以用来描述我的不确定性也给了我们一种量化信息的方式。
如果我确定一件事情要发生，我就不需要发送信息。如果有两件事各以50%的概率发生，我只需要发送1位。如果有64件事情等概率的发生，那么我们就需要6位。概率的分布越是集中，我们就越有机会用变长编码的方式去降低通信的成本。概率越是分散，那么需要的通信成本越大。
不确定性越大，当我们发现了什么事情发生的时候，我们学到的东西就越多。

交叉熵

在Bob出发去澳大利亚前不久，Bob和Alice结婚了，毫无疑问也是我虚构的。我自己都感到惊讶，也许是头脑中的另一种性格，Alice并不是一个爱狗者，而是一个爱猫者。尽管如此，他们还是能够找到沉迷动物的共同语言，并且拥有非常有限的词汇。

他们只以不同的频率说着相同的词汇。Bob经常说狗，而Alice经常说猫。
刚开始Alice用Bob的编码方式给我发消息。不幸的是，她用的成本本可以低很多的，因为Bob的编码是根据Bob的词汇分布优化的。Bob用的时候平均编码长度是1.75。而Alice用Bob的编码的话就变成了2.25。如果这两个人用的分布不是这么相似的话，Alice用的平均编码长度会更加长。
长度——用另一个分布的最佳编码，来通信的平均编码长度——叫做交叉熵。正式的，我们可以这样定义交叉熵：

$$H_p(q)=\sum_x q(x)\log_2(\frac{1}{p(x)})$$
在这里，交叉熵是关于爱狗者Bob的词频的爱猫者词频。

为了降低通信成本，我让Alice用她自己的编码。这降低了她的平均通信长度。但是这带来了一个新的问题：有时候Bob会无意的使用Alice的编码。令人奇怪的是，Bob用Alice的编码表现比Alice用Bob的编码更加糟糕。
所以，现在我们有四个量：

• Bob用他自己的编码($H(p)$= 1.75位)
• Ailce用她自己的编码($H(q)$=1.75位)
• Alice用Bob的编码($H_p(q)=2.25$位)
• Bob用Alice的编码($H_q(p)=2.375$位)

这个结果并不像想象中的那么直观。比如 $H_p(q) \neq H_q(p)$。能看出来这4个值之间的差别吗？
在下面的图中，每个子图各表示4种可能中的一种。每个子图像之前图一样可视化了平均消息长度。它们是方形的组织形式。水平的两幅图来自相同的分布，垂直的两幅图使用同一套编码。这让你视觉上方便的去对比。

你能看出来为什么 $H_p(q) \neq H_q(p)$? $H_q(p)$因为在分布 $p$ 下面有一个词（蓝色）非常的常见，但是因为在$q$下面非常不常见而得到了一个长的编码。另一方面$q$分布下的常见词（粉色）在$p$下面并不常见，但是这个差异没有这么的明显，所以$H_p(q)$就没有$H_q(p)$那么大。
恩，那么为什么我们要关心交叉熵？交叉熵给了我们一种表达两种分布差异的方法。$p$和$q$的差异有多大，$p$关于$q$的交叉熵就会比$p$的熵大多少。

反之亦然。

真正有趣的事情是熵和交叉熵之间的差异。这个差异是来自因为用了给别的分布优化的编码造成的。如果分布相同，这个差异就是0。随着分布间差异的变大，这个差值就会变大。
我们把这个差值叫做Kullback-Leibler分歧，或者直接叫KL分歧，$p$关于$q$的KL分歧是，$D_q(p)$，如下定义:

$$D_q(p) = H_q(p)-H(p)$$
KL分歧的有意思的地方是它就像两个分布之间的距离。衡量着两个分布之间的差异。(如果你认真的研究这个问题，你就会发现另一门叫做信息几何的学科)。
交叉熵和KL分歧在机器学习领域令人难以置信的有用。机器学习中，往往我们希望一个分布尽可能的和另一个分布相似。比如我们希望一个被预测的分布和想要的分布尽可能的相似。KL分歧很自然的在这里得到应用，所以它出现在机器学习的很多地方。

熵和多变量

让我们回到先前将天气和穿衣的例子。

我妈，像很多父母一样，有时候会担心我是否穿了合适的衣服。(她有理由担心——因为我经常在冬天不穿外套)。所以她常常想知道天气和我穿什么衣服。我要发送多少位来通信呢？
最简单的方式就是展开这个分布:

现在我们可以画出这些词的分布的最优编码以及计算平均消息长度。

我们把这个叫做$X$和$Y$的联合熵。定义成:

$$H(X, Y)=\sum_{x,y} p(x,y)\log_2(\frac{1}{p(x,y)})$$
这和我们之前看到的一般的分布是一样的，除了是两个变量而不是一个。
一个稍微好一点的理解的方式不是展开它，而是在第三维上战士编码长度。这样的话熵就是体积。

假设我妈已经知道天气了，比方说她可以从电视上查看天气。这样我需要发送多少的信息呢？
看上去我好像不管怎样也要发送说清我穿什么的信息吧。但是事实上我只需要发更少的信息，因为天气强烈的暗示着我穿了什么衣服。让我们分别考虑下雨天和出太阳的情况。

在这两种情况下，平均来说我都不需要发送多少的信息，因为天气给出了要获得正确就结果的辅助信息。当下雨的时候，我可以用根据下雨优化过的编码。当出太阳的时候，我可以用根据出太阳优化过的编码。在这两种个情况下，我都可以相对使用通用编码少发送信息。我要计算的平均信息量只要将这两个分布结合起来就可以了。

我们把这个叫做条件熵。如果用公式写出来，是这个样子的：

$$H(X|Y)=\sum_y p(y) \sum_x p(x|y) \log_2(\frac{1}{p(x|y)})=\sum_{x,y} p(x,y) \log_2 \frac{1}{p(x|y)}$$

交互信息

在上一部分，我们看到，知道一个变量，意味着通信另一个变量可以需要更少的信息。

一个不错的思考这个问题的方式是将信息想象成条。如果这些bars之间有共享的信息，那么它们会相互重叠。比如$X$和$Y$中的某些信息共享，$H(X)$和$H(Y)$就是重叠的条。因为$H(X,Y)$是$X$和$Y$中的信息，所以它是条$H(X)$和$H(Y)$联合。

一旦我们这样看待问题，很多事情的理解变得简单了。
比如，我们之前提到的通信$X$和$Y$(联合熵$H(X,Y)$)相比只通信$X$(边缘熵$H(X)$)花费更多的信息。但是如果你已知$Y$，那么你相对来说只需要更少的信息来通信$X$(条件熵，$H(X|Y)$)。

这看起来有点复杂，但是我们如果从bar的角度来看又变得简单了。$H(X|Y)$是我们要发送给已经知道$Y$的人来通信$X$所需要的信息，也就是只在$X$中的信息而不在$Y$中的信息。视觉上，这意味着$H(X|Y)$是$H(X)$中不和$H(Y)$重叠的部分。
你现在可以根据下图来看不等式$H(X,Y) \geq H(X) \geq H(X|Y)$。

另外一个等式$H(X,Y)=H(Y)+H(X|Y)$。这就是$X$和$Y$中的信息，等于$Y$中的信息加上$X$中不在$Y$中的信息。

再一次这个等式是很难想到的，但是从信息bar的重叠角度看这个问题又变得简单了。
到现在为止，我们已经用多种方式解释了$X$和$Y$中的信息。我们有在每个变量中的信息，$H(X)$和$H(Y)$。我们有两个量联合中的信息，$H(X,Y)$。我们有只在一个量中的信息$H(X|Y)$和$H(Y|X)$。其中在两个变量间共享的信息反复出现，信息之间的交集。我们把它叫做”交互信息”，$I(X,Y)$，定义如下：

$$I(X,Y) = H(X)+H(Y)-H(X,Y)$$
有这个定义是因为 $H(X)+H(Y)$中有两份交互信息，因为交互信息在 $X$和$Y$中都存在。而 $H(X,Y)$中只有一份。(考虑之前的bar图)。
和交互信息密切相关的一个量是变异信息。变异信息是指变量间不共享的信息。我们可以这样定义:
$$V(X,Y)=H(X,Y)-I(X,Y)$$
变异信息也有点意思，因为它也给了我们一个度量标准，变量间的一个距离的概念。如果知道一个量就知道另一个量，那么这两个量的变异信息就是0。变异信息随着变量之间的独立程度的增加而增加。
那么这和KL分歧有什么关系？它同样给了我们一个距离的概念。KL分歧给了我们同一个变量或者同一组变量的两个不同分布之间的距离度量。而变异信息给了我们一个联合分布的两个变量之间的距离度量。KL分歧衡量同一个分布，而变异信息衡量同一个分布中的不同变量。我们可以把以上讲到的不同的信息画到同一幅图中：

分数位

信息论中一个非常unintutitive的事情是我们可以有分数量的位。这很奇怪，有半个位意味着什么？
有一个简单的答案：往往我们关心的是期望消息长度，而不是某一个具体的消息长度。如果一半的时间发送1位，而另一半的时间发送2位，那么期望消息长度是1.5位。期望长度是分数没有什么好意外的。
但是这个答案避开了问题的关键。往往，最优编码长度是分数的，这意味着什么？
为了具体化，我们考虑一个概率分布，事件$a$发生的概率是71%，事件$b$发生的概率是29% 。最优编码使用0.5位来表示$a$，使用1.7位来表示$b$。如果我们要发送这样的编码是不可能的， 我们必须取整数的位，并期望发送1位。
但是如果我们想要每次发送多个位，我们其实可以做的更好。我们考虑从这个分布出发发送两个事件。如果独立的发送它们，我们需要2位。那么我们能做的更好吗？

一半的时间我们在通信$aa$，各21%的时间我们在发送$ab$和$ba$，而8%的时间我们通信$bb$。再一次，我们理想的编码涉及分数。

如果取整编码长度我们得到下图:

这个编码方案给了我们1.8的平均消息长度。这和我们之前独立的发送需要2位来说要少。另一种思考这个问题的方式是现在我们对于每个事件只需要通信0.9位。如果我们一次发送更多的事件，这个值会变得更小。当$n$趋向无穷大，由于取整造成的消息长度增加就会消失。而编码的位数就会接近熵。
进一步，$a$的理想编码长度是0.5位，$aa$的理想编码长度是1位。即使它是分数，理想编码长度也会增加。所以我们每次要通信多个事件，期望消息长度就会增加。
即使实际只能用整数的位，可以有分数位的信息长度也有很重要的意义。
(在实际应用中，人们使用在不同范围内都有效果的霍夫曼编码，基本上就是上面的方法，它处理分数位问题并不是非常优雅，和上面一样你需要对符号进行分组或者使用更加复杂的技巧来逼近熵的约束。算术编码稍有不同，但是它优雅的处理了分数位问题，使得期望消息长度逼近最优）。

总结

如果我们关心的最少的位，这里提到的思想很明显是相当基本的。如果我们关心数据压缩，信息论解答了核心问题并且给出了基础的抽象。但是假如我们不关心这些，除了好奇心还有其它什么？
信息论中的思想出现在很多的领域里面: 机器学习，量子物理，遗传学，热力学，甚至是赌博。这些领域的实践者一般不会因为想要压缩信息而关心信息论。他们关心是因为这些知识和他们的领域有密切的联系。量子纠缠可以用熵来解释。统计力学和热力学中的很多结论可以通过假设事件的最大熵不知道的前提下推导出来。赌徒的输或者赢跟KL分歧有直接联系，尤其是迭代设置。
信息论出现在所有这些地方，因为它提供了具体的，我们所要表达的很多事情的有根据的形式化。它给了我们衡量和表达不确定性的方法。两组判定之间有多大的差异，一个问题的答案可以告诉我们另一个问题什么东西：概率分布有多么的分散，概率分布之间的距离有多大，两个变量之间有多大的独立程度。有没有替代的相似的想法？有的。但是信息论中的想法干净，而且有很好的特性，以及一个有根据的出发点。在有些情景下，信息论中的观点就是你想要的，在很多其它情景下它也是这个混乱世界的一个很方便的解释。
机器学习是我知道的最多的领域，所以让我来讲一讲它吧。机器学习中的一个非常常见的任务就是分类。假如给我们一张图片，让我们预测图片里面是狗还是猫。我们的模型也许会告诉我们“80%的概率是狗，20%的概率是猫。”假如结果就是狗——那么我们只说80%概率是狗这个说法有多好？如果说85%的概率是狗，那么这种说法又提高了多少？
这是一个很重要的问题，因为我们需要一个概念去衡量我们模型的好坏，从而去优化它。我们需要提高什么呢？正确的答案往往跟我们使用模型的目的有关：我们只关心概率最大的那个结果？或者我们关心正确的结果概率有多大？有很大的概率得到错误的结果这样有多么的糟糕？没有一个标准的答案。因为不知道我们的模型到底多大程度上匹配我们最终需要的结果，所以往往不可能知道正确的答案。尽管并不是总是正确，结果表明交叉熵都是一个用来衡量模型好坏的一个不错的概念。很多时候我们不知道我们具体关心的是什么，但是交叉熵就是一个不错的概念。
信息给了我们一个新的强大的框架来看待世界。有时候它完美匹配我们手头的问题。也有时候尽管它并没有完美匹配，但是也非常有用。这篇文章只是写了一点信息论的皮毛——还有很多主题，比如说纠错编码，我们就完全没有提及——但是我希望我已经展示了信息论是一门很优美的学科，你并不需要感到害怕。

阅读材料

Claude Shannon的关于信息论的paper，通信的数学原理是卓越的工作。(它貌似在早期信息论文章中反复的出现。它是一个时代？没有页码限制？还是贝尔实验室的文化输出？)
Cover & Thomas的The element of information theory貌似是标准的材料，我发现它很有用。

感谢

非常感谢Dan Mane，David Andersen，Emma Pierson以及Dario Amodei。感觉他们关于本文仔细的有深度的评论。也感谢Michel Nielson，Greg Corrado，Youshua Bengio，Aaron Courville，Nick Beckstead, Jon Shlens(http://research.google.com/pubs/JonathonShlens.html), Andrew Dai, ChristianHoward,以及Martin Wattenberg的评论。
也感谢我最早的两个神经网络讨论班，得以演示我文中提到的想法。
最后感谢发现错误和失误的读者。尤其感谢Connor Zwick, Kai Arulkumaran, Jonathan Heusser, Otavio Good, 以及一个匿名的评论者。