【理论分析】线性预测器的等价性

论文：An Analysis of Linear Time Series Forecasting Models
作者：William Toner， Luke Darlow

1 摘要

尽管线性模型很简单，但它在时间序列预测中表现良好，即使是在与更深入、更昂贵的模型竞争时也是如此。已经提出了许多线性模型的变体，通常包括某种形式的特征归一化，以提高模型的泛化。本文分析了用这些线性模型体系结构可表示的函数集。通过这样做，我们证明了时间序列预测的几种流行的线性模型变体是等效的，并且在功能上与标准的无约束线性回归难以区分。 我们描述了每个线性变量的模型类。我们证明了每个模型都可以被重新解释为在适当增强的特征集上的无约束线性回归，因此在使用均方损失函数时承认封闭形式的解决方案。我们提供的实验证据表明，在检查模型学习几乎相同的解决方案，并最终证明，更简单的封闭形式的解决方案是优越的预测在72%的测试设置。

2 简介

线性模型定义:令$x\in r_l$是一个上下文向量。DLinear的工作原理是把x分解成“趋势”和“季节”分量。趋势分量是通过对x的分量取一个移动平均值来定义的。季节分量由残差$x_{seasonal}:=x-x_{trend}$给出。移动平均线被填充，这样它就保留了x的维度。然后，我们把x -季节性和x -季节性分开，把它们传递给单独的可学习的线性层。

贡献：
在本文中，我们深入研究了几个著名的线性时间序列预测模型的数学证明。我们充分描述了使用每个架构可表达的功能集。我们显示，有些引人注目的是，**它们本质上都是等效的:**对应于无约束或弱约束(通过特征增强)线性回归。最小二乘线性回归的凸性表明，这些模型的行为实际上应该是难以区分的。我们提供了支持这一假设的实验证据，表明在实践中，所有模型都趋向于相同的最优。此外，我们证明了最小二乘线性回归的封闭形式解的性能与梯度下降训练的解相当或更好。我们的贡献是:

• 数学证明，几种流行的线性时间序列预测模型本质上是相同的。
• 实验证据表明，当对相同的数据进行训练时，每个模型确实倾向于相同的解决方案，只是偏差参数不同。
• 定量证据表明，封闭形式的普通最小二乘(OLS)解决方案通常优于使用随机梯度下降训练的现有模型。

关注微信公众号，获取更多内容：

3 线性时间序列预测分析模型

为了本文的目的，我们将“模型类”称为由模型体系结构引起的函数的参数集。例如，一个没有隐藏层的单层线性神经网络的模型类为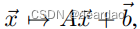
其中a和b的维数是合适的。在本文的剩余部分，我们称之为“线性”。在本节中，我们用线性模型定义预测任务。然后，我们分析了广泛使用的DLinear(第3.1.1节)和最近的SoTA FITS架构(第3.1.2节)。我们从数学上证明了这些模型与线性回归是等价的，因为它们具有相同的模型类。然后，我们在第3.2节中定义和讨论了用于时间序列预测的几种可逆数据归一化策略。这些归一化策略产生额外的线性模型变体，即RLinear、NLinear和FITS+IN (如Xu等人所说，即FITS与实例规范化）。

3.1 符号

• L: 上下文长度(输入序列中的时间步长)。
• c: 通道数(不同的时间序列)。
•T: 预测视界(预测未来的时间步长)。
• x: 上下文向量(历史数据)，∈R L×c。
• $y^{\prime }$: 目标向量(预测值)，$y^{\prime }\in R^{T\times c}$。

我们在第3节中看到的模型在其预测中没有明确地使用跨通道信息。通过这一点，我们的意思是目标的第i个通道只能使用上下文的第i个通道来预测。因此，为了提高清晰度，我们考虑c = 1(单变量)的情况，其中$x\in R^L$。

定义3.1(预测模型和模型类别)。预测模型是一个函数$f:R^L\to R^T$，它从给定的输入或上下文向量x’中生成预测y’。这些预测模型的集合形成一个模型类，记为M。

3.1.1 DLinear

DLinear模型定义:令$x^{\prime }\in R^L$是一个上下文向量。DLinear的工作原理是把x分解成“趋势”和“季节”分量。趋势分量是通过对x’的分量取一个移动平均值来定义的。季节分量由残差x_seasonal:=x−x_trend给出。移动平均线被填充，这样它就保留了x的维度。然后，我们把季节性和趋势性分开，把它们传递给单独的可学习的线性层。

引理3.2 (DLinear Model Class)。设M(DLinear)表示DLinear模型类，即可以表示为DLinear模型的函数集合$f:R^L\to R^T$。M(DLinear)正好等于仿射线性函数的空间。也就是说，所有形式为$Ax+b$的函数都可以表示为DLinear模型，反之亦然。

证明: 根据我们的定义，任何DLinear模型都可以写成Bx_seasonal +Cx_trend + c + d，其中$B,C\in R^{T\times L},c,d\in R$是DLinear的两个线性层的权矩阵和偏置。这可以表示为B(作x -x_trend) + C(x_trend) +c+d = B(x -Dx) + C(Dx) +c +d = (B -BD +CD)x +c +d，其中D是与填充移动平均线相对应的(方阵)矩阵(解释见附录D)。因此，我们已经证明了任何DLinear模型都可以用$Ax+b$的形式来表示。还需要证明相反的情况，即任何仿射线性映射都可以用DLinear模型的形式表示。设$Ax+b$是任意仿射线性映射。我们声称$Ax+b$可以表示为(B- BD+CD) x+ c + d。通过设置例如，c = b, d = 0，我们匹配了偏置项。通过设置B = C = A，我们匹配了权重矩阵，证毕。

3.1.2. FITS

FITS模型定义:令$x\in R^L$为上下文向量。FITS将实(离散)傅里叶变换(RFT)应用到x中。它将x映射为一个长度为$\lfloor L/2\rfloor +1$的复向量。接着输出维数为$\lfloor (L+T)/2\rfloor +1$的可学习复线性映射。在此之后，应用逆RFT映射到$R^{L+T}$。

注:根据Xu等人(2023)的提议，FITS可选地包括一个低通滤波器(LPF)来丢弃高频成分。我们最初的实验表明，使用LPF会导致性能下降——通过分析产生高性能的FITS设置，这一点得到了证实。因此，我们在没有LPF的情况下分析FITS。

注:与其他模型不同，FITS输出上下文向量的预测和重建。预测可以通过丢弃模型输出的前L个分量来获得。

定理3.3 (FITS模型类)。设M(FITS)表示FITS模型类，即可以表示为FITS模型的函数集$f:R^L\to R^T$。当$L\ge T-2$时，M(FITS)精确地等于仿射线性函数$Ax+b$的空间。

证明定理3.3有点复杂。重要的是，作为傅里叶变换、复线性映射和傅里叶反变换的组合，FITS是线性映射的组合，因此可以用$Ax+b$的形式表示。附录A.1中的证明表明当$L\ge T-2$时，A和b都是完全无约束的。这一点很重要，因为Xu等人(2023)的所有设置都使用大于或等于预测视界T的上下文。

3.2. 可逆数据规范化

可逆实例特征归一化最近被用于时间序列预测。“实例正常化”(在时间序列的背景下)由Kim等人(2021)提出。在本节中，我们将介绍三种这样的机制:实例规范(In)，可逆实例规范(RevIN)和NowNorm (NN)，这是我们给NLinear实现的规范化方案的名称。为了清楚起见，除了RevIN的可学习仿射映射之外，RevIN和IN是相同的——我们标记这种区别是因为通常不使用可选的可学习仿射映射(例如FITS)。我们将研究在与线性模型结合使用时，每种归一化如何限制模型类。

实例规范化

定义3.4(实例规范化)。给定一个上下文向量x和一个目标向量y，每个数据实例的实例归一化(IN)包括通过其均值µ(x)和标准差σ(x)对x进行归一化，对归一化的x′应用一个模型f，并将预测y’逆变换回原始尺度。正式地表示为:

其中ε是数值稳定性的一个小常数。

引理3.5 (Linear+IN)。设M(linear)可表示为结合实例归一化(定义3.4)的线性层的预测模型集合。M(线性)等于函数集合$f:R^L\to R^T$，可表示为$\tilde{A}x+b\sigma (x)$。$\tilde{A}$是一个每行之和为1的矩阵，σ(x)是x的标准偏差。

3.4 可逆实例规范化

第二种更一般的数据规范化形式被称为可逆实例规范(RevIN) (Kim et al.， 2021)。这种归一化的目的是允许预测模型处理随时间变化的时间分布。Li et al 表明，使用RevIN的简单线性模型能够在标准数据集上优于大多数深度模型。

定义3.6(可逆实例规范化)。给定一个上下文向量x和一个目标向量y，每个数据实例的可逆实例规范化(RevIN)包括一个两步规范化过程。首先，用它的均值µ(x)和标准差σ(x)对x进行标准化。随后，应用具有参数α和β的仿射变换，然后在变换后的x′上应用预测模型f。然后将该过程反向以原始尺度检索预测结果。正式地表示：

3.4.1 RLinear

RLinear是使用RevIN的线性模型(Li et al.， 2023)。引理3.7 (RLinear)。设M(RLinear)表示RLinear模型类，即可以表示为RLinear模型的函数集合$f:R^L\to R^T$。M(RLinear)精确地等于函数$\tilde{A}x+b\sigma (x)$的空间，其中$\tilde{A}$各行之和为1，其中σ(x)表示上下文向量x的标准差。

IN和RevIN给出了约束条件:(1)权重矩阵的行之和必须为1;(2)偏差由实例的标准差来衡量。

3.5 NowNorm

定义3.8 (Now-Normalisation)。给定一个上下文向量(context vector)与一个目标向量(target vector)相结合的x, NowNorm (NN)涉及到上下文的规范化，使得$x_L$，也就是x的最近值为零。明确地，
接下来，在将$x_L$添加回输出的每个分量之前，我们将预测模型f应用于规范化的x_norm上。正式地表示为:

3.5.1 NLinear

Nlinear是使用神经网络的线性模型(Zeng et al.， 2023)。
引理3.9 (NLinear)。设M(NLinear)表示NLinear模型类，即可以表示为NLinear模型的函数集合$f:R^L\to R^T$。M(NLinear)精确地等于线性函数$\tilde{A}x+b$的空间，其中$\tilde{A}$的每一行和为1。

将引理3.2和定理3.3的见解与本小节中提出的分析相结合，我们在模型类之间建立了以下等价:

4 讨论

我们的分析总结在表1中。当$L\ge T-2$时，FITS和DLinear在功能上等同于无约束线性回归(定义3.1)。在第3.2节中，我们研究了线性模型的模型类，这些模型使用时间序列分析的标准归一化过程之一。我们看到了使用规范化如何略微改变模型类。例如，NLinear等价于受限线性回归，其中权重矩阵的行之和必须为1。我们证明了Linear+IN, Linear+RevIN (RLinear (Li et al.， 2023))和FITS+IN(即(Xu et al.， 2023)中的设置)彼此等效，并且与NLinear的不同之处在于偏差被参数化为$b\sigma (x)$。也许最重要的是，每个模型类都可以被重新表述为增强特征集上的无约束线性回归，并且由于凹凸性，可以以封闭形式求解。

表1。DLinear、FITS、RLinear、NLinear和Linear模型的模型类总结。这里$\tilde{A}$表示一个矩阵，它的每一行之和必须为1，σ(x)表示上下文向量的分量的标准差。

凸性：我们讨论的每个模型都使用均方误差(MSE)损失函数进行训练(Xu et al.， 2023;Zeng et al.， 2023)。具有均方损失函数的线性回归是一个凸优化问题。这意味着训练损失是参数的凸函数。凸性的一个结果是存在一个唯一的全局最优，使训练损失最小化(唯一性要求训练数据是全秩的)。值得注意的是，这意味着给定相同的训练数据，这些模型应该通过适当的优化过程收敛到相同的解决方案。

闭式解：最小二乘线性回归的一个重要性质是它有一个封闭的解。关于如何计算线性回归的封闭形式解和表1中三个模型类的封闭形式解的概述，可以在附录D.2中找到。在第5节中，我们将封闭形式的解决方案称为普通最小二乘(OLS)模型，我们将确定每个模型如何与这种封闭形式的方法相匹配。

注:FITS有两种不同的训练模式。在模式1中，模型通过预测与目标之间的均方误差(MSE)进行训练。在模式2中，在损失中增加了一个附加项，即上下文向量和FITS重建之间的MSE。从经验上看，这两种设置具有相似的性能(Xu et al.， 2023)。在我们的分析和实验中，我们只考虑模式1。

5 实验

图1显示了4个训练好的线性模型变量加上封闭形式解(表示OLS+IN)的内部权重矩阵。所示的模型为RLinear、NLinear、DLinear+IN、FITS+IN(来自(Xu et al.， 2023)的FITS的SoTA变体)和OLS+IN。每个模型在ETTh1数据集上训练了50个epoch 1，上下文为720，预测水平长度为336。然后提取权重矩阵并使用相同的色标进行可视化。在所有情况下，学习到的矩阵几乎是相同的。线性+IN、RLinear、FITS+IN和OLS+IN的权值矩阵的相似度正好符合我们的假设，与前几节的理论和讨论相匹配。请注意，虽然NLinear lies是一个略有不同的模型类(见表1)，但学习到的矩阵仍然几乎相同。

图1所示。该图显示了所有四种模型经过实例归一化训练50次后裁剪的权重矩阵，并与它们相应的封闭形式解并列(最左)。这些显示了底层模型是多么相似。细微的差异会在一定程度上影响预测(参见图3)。

图2：在训练过程中，模型的权重矩阵如何倾向于OLS解决方案的演示。这是一个可视化的余弦相似度之间的给定模型的权重矩阵和确定的封闭形式的解决方案。

表2。长期多元预测结果，显示了本研究中所有模型的MSE值。绿色和蓝色高亮分别表示OLS较优和在给定模型的1个标准差范围内。Bolding表示给定数据集水平组合的最佳表现模型。