保形预测简介无分布不确定度量化

摘要

黑箱机器学习模型现在经常用于高风险环境，如医疗诊断，这需要对不确定性进行量化，以避免相应的模型故障。共形预测(又称共形推理)是一种用户友好的范例，用于为此类模型的预测创建统计严格的不确定性集/区间。关键的是，这些集合在无分布的意义上是有效的:即使没有分布假设或模型假设，它们也具有显式的非渐近保证。可以将保形预测与任何预训练模型(如神经网络)一起使用，以生成保证包含用户指定概率(如90%)的基本事实的集合。它易于理解，易于使用和通用，自然适用于计算机视觉，自然语言处理，深度强化学习等领域出现的问题。

这个动手介绍的目的是为读者提供一个工作的理解保形预测和相关的无分布不确定性量化技术与一个独立的文件。我们将引导读者了解保形预测的实际理论和示例，并描述其扩展到复杂的机器学习任务，包括结构化输出、分布移位、时间序列、异常值、弃权模型等。在整个过程中，有许多解释性的插图、示例和Python代码示例。每个代码示例都附带一个Jupyter笔记本，在实际数据示例中实现该方法。

1 保形预测

共形预测1-3是为任何模型生成预测集的直接方法。我们将用一个简短的、实用的图像分类示例来介绍它，并在后面的段落中进行一般解释。适形预测的概要如下。首先，我们从一个拟合的预测模型(如神经网络分类器)开始，我们将其称为f。然后，我们将使用少量额外的校准数据为该分类器创建预测集(一组可能的标签)，我们有时将此称为校准步骤。

形式上，假设我们有图像作为输入，它们每个都包含K个类中的一个。我们从输出每个类的估计概率(softmax分数)的分类器开始:f(x)∈[0,1]^K。然后，我们保留一个中等数量(例如，500)的在训练期间未见过的图像和类的新id对，(X1,Y1)，…， (Xn,Yn)，作为标定数据。使用f和校准数据，我们试图构建一个可能标签的预测集C(Xtest)∧{1，…， K}在以下意义上是有效的:

其中(Xtest,Ytest)为来自同一分布的新测试点，α∈[0,1]为用户选择的错误率。换句话说，预测集包含正确标签的概率几乎正好是1-α;我们称此属性为边际覆盖，因为概率是在校准点和测试点的随机性上的边际(平均)。图1是Imagenet数据集上的预测集示例。

图1:Imagenet上的预测集示例。我们展示了狐松鼠类的三个难度逐渐增加的例子，以及由共形预测生成的预测集(即C(Xtest))。

为了从f和校准数据构造C，我们将执行一个简单的校准步骤，只需要几行代码;参见图2的右面板。现在我们更详细地描述校准步骤，介绍一些稍后会有所帮助的术语。首先，我们设置适形分数
等于1减去真类的softmax输出。当真实类的softmax输出较低时，即模型严重错误时，得分较高。接下来是关键的一步:定义q为(n+1)(1-α)/n经验分位数s1，…sn,其中，上限函数(q)是否等于1 -α分位数，但校正较小)。最后，对于一个新的测试数据点(其中Xtest已知，但Ytest未知)，创建一个预测集C(Xtest)= {y: f (Xtest)y≥1 ?q}，它包括所有具有足够高的softmax输出的类(见图2)。值得注意的是，无论使用哪种(可能不正确的)模型或数据的(未知的)分布如何，该算法给出的预测集都保证满足(1)。

Remarks

让我们考虑一下C的解释。函数C是集值的——它接受一个图像，并输出一组类，如图1所示。模型的softmax输出有助于生成集合。该方法针对每个特定的输入自适应地构建不同的输出集**。当模型不确定或图像本质上是难样本时，集合变得更大**。这是我们想要的属性，因为集合的大小为您提供了模型确定性的指示器。此外，可以将C(Xtest)解释为一组合理的类，映像Xtest可以分配给这些类。最后，C是有效的，这意味着它满足(1).1 中C的这些特性可以很自然地转化为其他机器学习问题，比如我们将看到的回归。

着眼于泛化，让我们详细回顾一下我们的分类问题中发生了什么。首先，我们得到了一个模型，它有一个内置的，但启发式的不确定性概念:softmax输出。softmax输出试图度量每个类的条件概率;换句话说，softmax向量的第j项估计P(Y = j | X = X)，类j在输入图像X上有条件地出现的概率。然而，我们不能保证softmax输出是好的;它们可能是任意过拟合的，或者是不可信的。因此，我们没有采用表面值的softmax输出，而是使用holdout集来调整其不足之处。

保留集包含n≈500个模型在训练期间从未见过的新数据点，这使我们能够对其性能进行诚实的评估。调整涉及计算保形分数，当模型不确定时，保形分数会增长，但它们本身不是有效的预测区间。在我们的例子中，共形分数是1减去真实类的softmax输出，但通常情况下，分数可以是x和y的任何函数。分数的α分位数。在这种情况下，分位数有一个简单的解释-当设置α =0.1时，至少90%的ground truth softmax输出保证高于级别1 ?(我们在附录D中严格地证明了这一点)。利用这一事实，在测试时，我们获得了新图像Xtest的softmax输出，并收集了输出大于1 -q，得到预测集C(Xtest)。由于新的真类Ytest的softmax输出保证大于1 -q，在概率至少为90%的情况下，我们最终得到了式(1)中的保证。

适形预测说明

正如我们在总结中所说，适形预测并不特定于softmax输出或分类问题。事实上，保形预测可以被看作是一种从任何模型中获取不确定性的启发式概念并将其转换为严格概念的方法(见下图)。适形预测并不关心潜在的预测问题是离散/连续还是分类/回归。

接下来，我们概述了一般输入x和输出y的保形预测(不一定是离散的)。

和前面一样，这些集合满足(1)中的有效性属性，对于任何(可能没有信息的)分数函数和
(可能未知)数据的分布。下面我们正式说明覆盖保障。

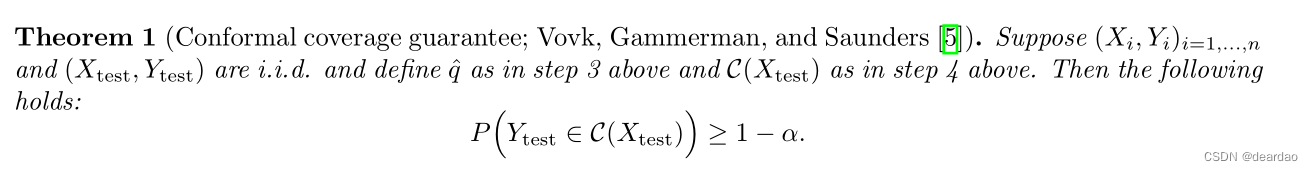
在附录D中有一个证明和一个包含(1)上界的陈述。我们注意到以上只是保形预测的一种特殊情况，称为分裂保形预测。这是最广泛使用的适形预测版本，它将是我们的主要焦点。为了完善这幅图，我们在后面的第6节中全面描述保形预测，并在第7节中概述文献。

分数函数的选择

乍一看，这似乎好得令人难以置信，持怀疑态度的读者可能会问以下问题:
怎么可能构建一个统计上有效的预测集，即使底层模型的不确定性的启发式概念是任意糟糕的?

让我们给出一些直觉来补充附录d中证明的数学理解。粗略地说，如果分数si正确地将输入从最低到最高的模型误差排序，那么结果集对于简单的输入将更小，对于困难的输入将更大。如果分数很差，也就是说它们不接近这个排名，那么这些集合将是无用的。例如，如果分数是随机噪声，则集合将包含标签空间的随机样本，其中该随机样本足够大以提供有效的边际覆盖。这说明了关于保形预测的一个重要的潜在事实:尽管保证总是成立，但预测集的有用性主要由分数函数决定。这并不奇怪——分数函数包含了我们所知道的关于问题和数据的几乎所有信息，包括底层模型本身。例如，在分类问题和回归问题上应用适形预测的主要区别在于分数的选择。对于单个底层模型，也有许多可能的得分函数，它们具有不同的属性。因此，构造正确的分数函数是一个重要的工程选择。接下来我们将展示几个优秀分数函数的例子。

2 适形程序的例子

在本节中，我们将给出在许多设置中应用的保形预测示例，目的是为读者提供实际部署的技术库。请注意，在本节中我们将只关注一维Y，较小的适形分数将对应更多的模型置信度(这样的分数称为不符合分数)。更丰富的设置，例如高维Y，复杂(或多重)的错误概念，或者不同的错误造成不同的损失，通常需要风险控制的语言，在A部分概述。

自适应预测集分类

让我们从对第1节中的分类示例的改进开始我们的示例序列。之前的方法产生的预测集平均大小最小[6]，但它倾向于掩盖难的子组而覆盖容易的子组。在这里，我们开发了一种不同的方法，称为自适应预测集(APS)，以避免这个问题。我们将遵循[7]和[4]。

作为这个新过程的动机，请注意，如果softmax输出f (Xtest)是Ytest|Xtest的完美模型，我们将贪婪地包括得分最高的类，直到它们的总质量刚刚超过1-α。

正式地，我们可以将这个oracle算法描述为

而π(x)是{1，…， K}将f (Xtest)从最可能到最不可能排序。然而，在实践中，这个过程不能提供覆盖，因为f - (Xtest)并不完美;它只是给我们提供了一个关于不确定性的启发式概念。因此，我们将使用保形预测将其转化为不确定性的严格概念。

接下来，我们定义一个受oracle算法启发的score函数:

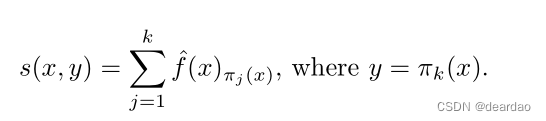
换句话说，我们贪婪地在集合中包含类，直到达到真正的标签，然后停止。与第1节的分数不同，这一节使用了所有类的softmax输出，而不仅仅是真正的类。

下一步，与所有保形过程一样，设q =Quantile(s1，…， sn; (n + 1)(1 -α)/n)。这样，我们将形成预测集{y: s(x, y)≤q}，稍加修改以避免零大小集:

图3显示了实现此方法的Python代码。与往常一样，这些不确定性集(具有平局)满足(1)。参见[4]了解细节和重大的实际改进。

图3

图4:Eq.(3)中自适应预测集算法的可视化。从最可能到最不可能包括类，直到它们的累积softmax输出超过分位数。

共形分位数回归

接下来，我们将按照[8]中的算法，展示如何将不确定性纳入具有连续输出的回归问题。我们使用分位数回归[9]作为基础模型。提醒一下，分位数回归算法试图对x的每个可能值学习Ytest|Xtest = x的γ分位数。我们将真分位数称为tγ(x)，拟合模型称为tγ(x)。由于根据定义，Ytest|Xtest = x以5%的概率落在t0.05(x)以下，以5%的概率落在t0.95(x)以上，我们可以期望区间为t´0.05(x)， t´0.95(x)达到大约90%的覆盖率。然而，由于拟合的分位数可能不准确，我们将它们统一起来。符合分位数回归的Python伪代码见图5。

在训练一个算法输出两个这样的分位数(这可以用标准损失函数完成，见下文)之后，tα/2和t1?α/2，我们可以将分数定义为y与其最近的分位数之差，
在计算我们的校准集上的分数并设置@ q =Quantile(s1，…， sn; (n + 1)(1 -α)/N)，我们可以通过取

直观地说，集合C(x)只是将分位数之间的距离增加或缩小q来实现覆盖。

图6：公式(4)中保形分位数回归算法的可视化。我们通过在校准步骤中选择的常数q 来调整分位数。

和前面一样，C满足Eq.(1)中的覆盖性质。但是，与我们之前在第1节中的例子不同，C不再是类的集合，而是r中的连续区间。分位数回归并不是得到这种连续区间的唯一方法。然而，这通常是最好的方法，特别是如果事先知道α。原因是，即使没有适形预测，通过分位数回归生成的区间，即[$t_{\alpha /2}(x)，t_{1-\alpha /2}(x)$]，一开始就有很好的覆盖率。此外，它们具有渐近有效的条件覆盖(我们将在第3节中解释这个概念)。这些属性通过保形过程传播，并导致具有良好性能的预测集。

分位数回归的一个吸引人的特点是，它可以很容易地添加到任何基本模型上，只需将损失函数更改为分位数损失(非正式地称为弹球损失)。

读者可以认为分位数回归是l1 -范数回归的推广:当γ =0.5时，损失函数减少到L0.5 = |t³γ(x) ?Y |/2，它鼓励t_0.5(x)收敛到条件中值。改变γ只是修改L1规范，如上图所示，以其他分位数为目标。在实践中，为了回归到分位数，可以在任何算法(如神经网络)的末尾使用分位数损失而不是MSE。

关注微信公众号，获取更多资讯内容：