由于中国没有实现资本项下的可自由兑换，目前人民币的外汇交易存在境内及境外两个市场。在境内交易的CNY和境外交易的CNH，本质都是人民币，从这个角度上看，两者具有高度相关性。但是由于两者的市场形态、监管细节、参与机构、流动性等等因素都不尽相同，使得两者长期存在或大或小的价差。观察历史走势图，两者之间的价差有着明显的均值回复现象，这意味着CNY-CNH两者的时间序列大概率存在协整关系。如果真的存在协整关系，那这协整关系是否稳定并可持续预测？基于协整分析的配对交易，在CNY-CNH的外汇即期上是否能有效提高收益？
这次练习手稿，就以JoinQuant【协整搬砖策略】的框架为参考，看看CNY-CNH的协整关系具体情况。据此判断能否运用配对交易策略(Spread_Trading)来提高USDCNY外汇交易的收益。
本文主要的参考文章如下：
【量化课堂】基于协整的搬砖策略
https://www.joinquant.com/view/community/detail/e11fcec811670158d771b64eb8176744
协整关系（cointegration）和配对交易https://zhuanlan.zhihu.com/p/158871695
目录
4.2 固定区间内的协整关系搜索函数、滑动时间窗口的协整寻优函数
1. 策略思路：
设代表USDCNY序列，
代表USDCNH序列。（此处Y用大写，x用小写是为了跟后续用statsmodels的api时保持一致）
假设CNY和CNH的关系遵从下列关系式，且CNY、CNH存在协整关系，则
，这个序列为平稳序列。
既然平稳，也就意味着
存在均值回归的性能(暂时不考虑条件异方差的问题）。对该残差序列进行标准化后，设定偏离该序列均值上下一个标准差为信号产生条件。
高偏信号：
当高于并偏离上方界限，
根据均值回复的假设，大概率会回落至均值水平，也就是说，
方程式的数值会减小。这就存在两个可能：
1）下跌走势中，USDCNY() 比 USDCNH(
)下跌更快；
2）上涨走势中，USDCNY() 比 USDCNH(
)上涨更慢；
交易操作：卖出USDCNY，买入USDCNH
低偏信号：
当低于并偏离下方界限，
根据均值回复的假设，大概率会上涨回调至均值水平，也就是说，
方程式的数值会减小。这就存在两个可能：
1）下跌走势中，USDCNY() 比 USDCNH(
)下跌更慢；
2）上涨走势中，USDCNY() 比 USDCNH(
)上涨更快；
交易操作：买入USDCNY，卖出USDCNH
2. 策略风险
该策略的本质，其实就是【做多--】或者【做空】【一对金融标的】的【价差】。
本文的【一对金融标的】为CNY,CNH的即期汇率。【价差】为CNY减去经过回归系数调整的CNH，也就是。
当高偏信号产生，标示着该价差高于正常水平，可以【做空价差】，也就是卖出该价差。而配对交易中，卖出价差意味着需要同时操作两个货币对：卖出USDCNY，买入USDCNH。等待价差回归后再买入USDCNY，卖出USDCNH获利了结。低偏信号反向操作即可。
或许有人会对高偏信号产生时，如果处于上涨走势，为什么还需要卖出USDCNY。原因在于配对交易中，更多的是在交易涨跌的速度，而不是涨跌的方向。当同处于上涨走势，你【做空价差】，也就是说卖出USDCNY带来亏损(USDCNY处于上涨走势中）的同时，由于【高偏信号】意味着买入的USDCNH会带来更大金额的盈利（同处于上涨趋势的USDCNH，上涨速度更快）。
协整关系是历史数据回归检测得出的关系，配对交易的根本假设是：当前的协整性质，会在未来一段时间内持续。但是未来协整性质如果不存在了，价差的残差序列无法向均值回归，那么这个交易策略产生的信号也就会带来亏损。毕竟CNY和CNH虽然本质都是人民币，但是由于外汇管制的存在，他们是无法自由转换。在这个配对交易策略中，你会同时持有CNY和CNH的头寸。一旦价差无法按预期收敛，甚至存在价差完全反向运作，那这两份头寸同时产生的亏损就很客观了。
3. 协整知识
3.1 跑的了和尚跑不了庙---说的就是协整
学生时代有学过协整，不过那时候由于编程能力有限，而且视频教学资料也不如现在多。所以多数时候只能两眼懵圈看着那些写满公式的协整理论书籍。近来重温协整，看到有人用【醉汉与狗】或者【母鸡和小鸡】关系来介绍协整的视频，深感受用。
我也尝试用中国的一句古话来聊聊我对协整的理解----【跑得了和尚跑不了庙】。
我们国内有大大小小的庙宇分布在各个城市，位置相对随机，并没有一定的规律。我们无法通过拟合一条曲线，来稳定预测每家庙宇的具体物理位置。
但是如果我们只是考虑和尚--庙之间【距离】这一关系，则可以肯定他们大概率会生活在以庙为中心的特定半径周围。【距离】这一序列，起始就是把和尚的【物理位置】序列，减去庙宇的【物理位置】序列得到的【残差】序列。这一序列数值范围大概会处于[0,若干公里]的数值区间内，而且该序列大概率是平稳序列。
a) 睡觉吃饭----离庙十米八米；
b) 买菜挑水----离庙百十米到一两公里；
c) 化缘宣佛----离庙三五公里；
d) 到同一地区其他庙走访-----离庙十多公里；
根据a,b,c,d这些情形，我们可以判断和尚和庙的【距离】一般来说，存在着【协整】关系。他们离开所在庙宇一段距离之后，会存在【返回庙宇】的需要，类似于【协整】里面所说，序列误差存在的均值回复的需要。
e) 转到其他庙宇挂单-----小则离庙几百米，远则几百公里。但是无论距离，基本上很少回到原来的庙宇。
f) 还俗----小则离庙几百米，远则几百公里。但是无论距离，基本上很少回到原来的庙宇。
根据e,f这些情形，我们也能看出，哪怕和尚、庙之间的【距离】再平稳，也有可能会发生稳定性被打破而变成非平稳序列。e这情形中，和尚到其他庙宇挂单之后，很有可能要花三年五载才能回归原来庙宇，有的甚至就永远不回归原来庙宇了。两序列的底层逻辑发生极大变化，【距离】序列也就变成了非平稳序列，要麽收敛回归均值时间超出预期。要么就根本不回归。f这情形除非偶尔回去探望怀旧一下，否则【距离】基本不会回归到百十米的初始均值了。
3.2 协整应用的一般场景
在对时间序列进行分析时，由于一些序列自身属于非平稳序列 (所谓平稳，一般指弱平稳，也即该序列的一阶<均值>、二阶矩<方差>，不随时间而改变）。这些非平稳序列，由于均值方差会产生不可预期的波动，因此无法对这些单个序列进行很好的预测。（例如，在用AR自回归分析对序列分析时，非平稳序列无法收敛，该序列无法用于对未来一段时间的预测）
但是根据协整（协同之后，一二阶矩就规整稳定了）理论，我们可以将两个或者多个序列进行回归，回归后的残差序列很有可能就成为平稳序列。这样，我们就可以通过他们的协同回归关系，来观察它们的相互关系并对其走势进行预测。 Cointegrationhttps://corporatefinanceinstitute.com/resources/knowledge/other/cointegration/
一般来说，对于两个序列回归后的残差序列，我们可以用AEG（增强恩格尔-格兰杰）方法来检验该残差序列的平稳性，但是一旦涉及多个序列的协整关系检验，AEG无法胜任。我们需要用Johansen Test。具体原因可以参考上面的链接。
3.3 协整检验步骤解析
在Python中的Statsmodels库中，有一个coint【cointergation】的协整检验函数。该函数的帮助信息显示：【method : {'aeg'} Only 'aeg' (augmented Engle-Granger) is available.】，意味着我们如果调用coint方法来对序列进行协整检验，只能处理两两配对的序列关系。
判断序列平稳性：单位根检验
为什么序列存在单位根是非平稳时间序列？----统计模拟https://www.zhihu.com/question/22385598/answer/2032789620为什么序列存在单位根是非平稳时间序列？-----公式简介https://www.zhihu.com/question/22385598/answer/297245327 下面通过一个简单的案例来看看coint方法和AEG两步法的异同。(下面只是辅助对coint方法和AEG的理解，高手可自动略过）。
我们先创建了两个随机序列，其中一个序列x进行累计求和之后得到X。把X与另一序列相加，从而得到我们的Y。直接使用stasmodels自带的时序分析工具里的协整关系检验(coint)，我们可以得到coint计算出来的两序列的pvalue。
然后我们还会单独按照Engle-Granger方法，对两个序列进行回归得到关系式。用计算出来的
，
代回
和
序列中，得到该回归的残差序列。也就是
项。对该残差序列进行单位根检验。
观察两次操作的检验值，我们可以看到结果大同小异。由此我们大致理解了coint方法的具体工作机制，代码如下：
import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import coint,adfuller
import matplotlib.pyplot as plt
import statsmodels.api as sm
np.random.seed(50) #生成指定的基于第50堆种子的随机数
x=np.random.randn(1,1000)
y=np.random.randn(1,1000)
y=pd.DataFrame(y).T #转成数据框格式后，转置成列
x=pd.DataFrame(x).T
x=np.cumsum(x) #按顺序逐行将x列进行累加，然后重新赋值给x。此处隐含了x序列进行一阶差分后，是一个平稳的随机序列。
Y=x+y #把累计和序列，加上平稳的随机序列，Y必然也是一阶差分后平稳的序列，也就是一阶单整序列
plt.plot(Y)
plt.plot(x)
result=coint(Y,x)
print("statsmodels自带coint方法的检验结果（第一个数字为检验t值，第二个数字为p值，array分别为1%，5%，10%的临界值）\n",result)图1: 随机序列X，Y
statsmodels自带coint方法的检验结果：
（第一个数字为检验t值，第二个数字为p值，array分别为1%，5%，10%的临界值）
(-30.773192613015876, 0.0, array([-3.90743646, -3.34225305, -3.04869817]))
图2：示范序列的残差图
sm.add_constant(x)含义
X=sm.add_constant(x) #为自变量序列添加常数值为1的序列
linear_result=(sm.OLS(Y,X)).fit() #调用最小二乘法进行回归拟合
print(linear_result.summary())
residual=Y-x*(linear_result.params.iloc[1]) -linear_result.params.iloc[0] #提取残差序列
adf_result=adfuller(residual) #对残差序列进行ADF平稳检验
print(adf_result)
OLS Regression Results
==============================================================================
Dep. Variable: 0 R-squared: 0.995
Model: OLS Adj. R-squared: 0.995
Method: Least Squares F-statistic: 2.175e+05
Date: Wed, 21 Sep 2022 Prob (F-statistic): 0.00
Time: 13:24:17 Log-Likelihood: -1428.7
No. Observations: 1000 AIC: 2861.
Df Residuals: 998 BIC: 2871.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0633 0.059 1.066 0.287 -0.053 0.180
0 1.0020 0.002 466.369 0.000 0.998 1.006
==============================================================================
Omnibus: 3.265 Durbin-Watson: 1.940
Prob(Omnibus): 0.195 Jarque-Bera (JB): 2.753
Skew: -0.009 Prob(JB): 0.252
Kurtosis: 2.744 Cond. No. 51.3
==============================================================================
（第一个数字为检验t值，第二个数字为p值，大括号内分别为1%，5%，10%的临界值）
(-30.757773163618776, 0.0, 0, 999, {'1%': -3.4369127451400474, '5%': -2.864437475834273, '10%': -2.568312754566378}, 2770.320163124055)
由上面两次操作得到的p值可以看出，coint的结果与按照恩格尔--格兰杰两步法进行检验的结果结果基本相同。
4. 多货币对协整关系分析
4.1 数据预处理
根据各自数据的结构，对数据进行初步清理。同时加入后续处理需要用到的年份信息列。
pairs_df=pd.read_csv("C:\\Users\\你的电脑ID\\Desktop\\Currency Pair Cointed.csv",parse_dates=True,index_col='Date')
temp=(pairs_df.columns)
replace_result=list(map(lambda x:x.split(" ")[0],temp)) #由于我下载的数据columns内含有除了货币对信息外的其他文字，这里对columns进行初步清理
pairs_df.columns=list(replace_result)
pairs_df.sort_index(ascending=True,inplace=True) #按照Date Index进行升序排序
pairs_df.fillna(method="ffill",inplace=True) #遇到缺失值，用前一天价格进行填充
pairs_df=pairs_df.assign(Year="") #加入年份信息列，便于后续按年进行循环画图分析
pairs_df['Year']=pd.DatetimeIndex(pairs_df.index).year
4.2 固定区间内的协整关系搜索函数、滑动时间窗口的协整寻优函数
由于本文数据集含有多个货币对的即期价格序列，仿照JointQuant的思路做了一次在多币种中寻找最优协整货币对的分析。本数据集的货币对包括：['USDCNH', 'USDSGD', 'USDCAD', 'USDJPY', 'CNY']。
def find_cointegrated_pairs(df):
n=df.shape[1]
pvalue_matrix=np.ones((n,n))
keys=df.columns
pairs=[]
for i in range(n):
for j in range(i+1,n):
cur1=df[keys[i]]
cur2=df[keys[j]]
result=coint(cur1,cur2)
pvalue=result[1]
pvalue_matrix[i,j]=pvalue
if pvalue<0.30:
pairs.append([keys[i],keys[j],pvalue])
return pvalue_matrix,pairs
def find_best_cointegrated_period(df,start,end,interval):
best_cointegrated_period=[]
for days in range(start,end,interval):
i=0
while i+days < len(df):
temp_range=df[i:(i+days)]
i+=40
pvalue,pairs=find_cointegrated_pairs(temp_range)
best_cointegrated_period.append({"Date":[temp_range.index[0],temp_range.index[-1]],"pvalue_matrix":pvalue,"pairs":pairs,"interval":days})
print(f"All the cointegrated pair in Days_interval {days} is Done!!")
return best_cointegrated_period
固定区间内的协整关系搜索函数:find_cointegrated_pairs(df)
将数据框内的列标签（列表签为货币对信息）内的货币对，通过循环两两配对，用coint来检验它们的协整性，把返回的计算结果（pvalue_matrix等）放入pairs列表内。pvalue越低代表着协整关系越可信，一般我们会选择低于0.05的pvalue。本搜索函数里设置了所有低于0.30的pvalue都放入列表，主要是为了在移动时间窗口寻优时避免由于没有pvalue值而报错。
滑动时间窗口的协整寻优函数:find_best_cointegrated_period()
将数据集内的数据，按照不同的时间颗粒度进行协整关系的搜索。然后把日期区间信息、货币对信息、该货币对所对应的协整pvalue等存入列表内。该列表内的信息按照pvalue值来排序后，可以获取哪个货币对在哪段时间内具有最优的协整关系。
颗粒度的意思如下图示意（本次练习的颗粒度分为半年、一年两种）：
图3： 颗粒度示意图
4.3 3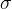
去极值函数、Z-Score函数
def sigma_filter(series,n=3):
mean=series.mean()
std=series.std()
max_band=mean+n*std
min_band=mean-n*std
return np.clip(series,min_band,max_band)
def get_zscore(series):
mean=series.mean()
std=series.std()
zscore = (series-mean)/std
return zscore 通过sigma_filter函数把残差序列位于3个标准差外的极值（我们暂定把3个标准差外的定为极值），用3个标准差的值来代替，从而达到清理极值的目的。
通过get_zscore函数，把残差序列进行标准化。标准化之后，我们设定上下限分别为1和-1，上偏或者下偏这一区间的值，可以成为我们【做多】或者【做空】货币对的信号。
4.4 最优协整货币对热力图
1-pvalue越大，颜色越深，也就是说pvalue值越小。而pvalue值越小，代表了该货币对协整关系的可信度越高。由下图我们可以看出对于2010年至2022年9月的外汇价格数据序列，有两个货币对的颜色是处于深红区间：【USDCNH--CNY】、【USDSGD--USDCAD】
heat_map_df=pairs_df[['USDCNH','USDSGD','USDCAD','USDJPY','CNY']]
fig3,ax3=plt.subplots(figsize=(10,6))
pvalue,pairs=find_cointegrated_pairs(heat_map_df)
print(pvalue,'\n',pairs)
ax3=sns.heatmap(1-pvalue,xticklabels=heat_map_df.columns,yticklabels=heat_map_df.columns,cmap='RdYlGn_r',mask=(pvalue==1))
ax3.tick_params(rotation=35)
图4：货币对协整关系热力图
4.5 滑动时间窗口寻找最优协整货币对
运行下列代码，我们可以打印出前50个pvalue值。可以看出多数时间内，CNY-CNH的协整关系的可靠性（pvalue较低）都处于较高水平。由此，我们相对放心的开始有针对性的研究CNY-CNH这两个货币对之间的协整关系。
best_cointegrated_period=find_best_cointegrated_period(pairs_df,126,254,126)
temp_df=pd.DataFrame(best_cointegrated_period)
temp_df=temp_df.assign(best_pvalue="",best_pair="")
ratio_df=temp_df['pairs']
for i,item in enumerate(ratio_df): #['pairs']
if item==[]:
continue
else:
row_lst=[]
for j,item2 in enumerate(item):
row_lst.append({'pvalue':item2[2],'row_pair':(item2[0]+"--"+item2[1])})
row_lst=pd.DataFrame(row_lst)
sorted_row_lst=row_lst.sort_values('pvalue',ascending=True)
best_pvalue=float(sorted_row_lst['pvalue'][0])
best_pair=sorted_row_lst['row_pair'][0]
temp_df['best_pvalue'][i]=best_pvalue
temp_df['best_pair'][i]=best_pair
temp_df=temp_df[['Date','best_pair','best_pvalue','interval']]
temp_df=temp_df[temp_df['best_pvalue']!=""]
temp_df=temp_df.sort_values('best_pvalue',ascending=True,ignore_index=True)
print(temp_df.head(50))
print(temp_df[temp_df['best_pair']=='USDCNH--CNY'].count())
print(temp_df[temp_df['best_pair']=='USDCNH--CNY'][(temp_df['Date'].apply(lambda x:x[0]))>"2020-01-01"].count())
print(temp_df[temp_df['best_pair']=='USDCNH--CNY'][(temp_df['Date'].apply(lambda x:x[0]))>"2020-01-01"][temp_df['interval']==252].count())148个最优协整结果中，USDCNY----USDCNH货币对共有82次，占比55%；其中2020年后的最优协整结果有11个，2020年后按【年】颗粒度的最优协整结果为5个。
Date best_pair best_pvalue interval 1 2017/11/6 2018/10/23 USDCNH--CNY 0.00000000000000000000 252 2 2018/1/1 2018/12/18 USDCNH--CNY 0.00000000000000000000 252 3 2021/1/25 2022/1/11 USDCNH--CNY 0.00000000000000000000 252 4 2018/2/26 2018/8/20 USDCNH--CNY 0.00000000000000000017 126 5 2012/4/30 2012/10/22 USDCNH--CNY 0.00000000000000000023 126 6 2014/8/18 2015/2/9 USDCNH--CNY 0.00000000000000457134 126 7 2014/12/8 2015/6/1 USDCNH--CNY 0.00000000000001647930 126 8 2021/1/25 2021/7/19 USDCNH--CNY 0.00000000000006629030 126 9 2021/3/22 2021/9/13 USDCNH--CNY 0.00000000000007134790 126 10 2018/1/1 2018/6/25 USDCNH--CNY 0.00000000000023687100 126 11 2016/12/5 2017/11/21 USDCNH--CNY 0.00000000000119267000 252 12 2017/9/11 2018/3/5 USDCNH--CNY 0.00000000000144847000 126 13 2020/11/30 2021/5/24 USDCNH--CNY 0.00000000000197620000 126 14 2021/5/17 2021/11/8 USDCNH--CNY 0.00000000000283685000 126 15 2013/2/4 2013/7/29 USDCNH--CNY 0.00000000001180360000 126 16 2014/3/3 2014/8/25 USDCNH--CNY 0.00000000007407610000 126 17 2017/9/11 2018/8/28 USDCNH--CNY 0.00000000368205000000 252 18 2017/7/17 2018/7/3 USDCNH--CNY 0.00000000390472000000 252 19 2020/8/10 2021/7/27 USDCNH--CNY 0.00000000939854000000 252 20 2016/1/4 2016/12/20 USDCNH--CNY 0.00000001876080000000 252 21 2020/4/20 2021/4/6 USDCNH--CNY 0.00000002299730000000 252 22 2018/8/13 2019/7/30 USDCNH--CNY 0.00000004421510000000 252 23 2018/2/26 2019/2/12 USDCNH--CNY 0.00000004937870000000 252 24 2019/11/4 2020/10/20 USDCNH--CNY 0.00000005568210000000 252 25 2018/4/23 2019/4/9 USDCNH--CNY 0.00000005785280000000 252 26 2016/1/4 2016/6/27 USDCNH--CNY 0.00000011527400000000 126 27 2017/5/22 2018/5/8 USDCNH--CNY 0.00000025464100000000 252 28 2013/5/27 2013/11/18 USDCNH--CNY 0.00000086508100000000 126 29 2016/12/5 2017/5/29 USDCNH--CNY 0.00000348515000000000 126 30 2016/8/15 2017/8/1 USDCNH--CNY 0.00000942823000000000 252 31 2020/10/5 2021/3/29 USDCNH--CNY 0.00000956229000000000 126 32 2017/11/6 2018/4/30 USDCNH--CNY 0.00000998784000000000 126 33 2010/10/18 2011/4/11 USDCNH--USDSGD 0.00002220470000000000 126 34 2016/4/25 2016/10/17 USDCNH--CNY 0.00002316370000000000 126 35 2013/7/22 2014/7/8 USDCNH--CNY 0.00002802500000000000 252 36 2013/9/16 2014/9/2 USDCNH--CNY 0.00002810870000000000 252 37 2014/4/28 2014/10/20 USDCNH--CNY 0.00003156020000000000 126 38 2019/12/30 2020/12/15 USDCNH--CNY 0.00003312210000000000 252 39 2017/7/17 2018/1/8 USDCNH--CNY 0.00003678170000000000 126 40 2018/10/8 2019/9/24 USDCNH--CNY 0.00003851240000000000 252 41 2014/6/23 2014/12/15 USDCNH--CNY 0.00009510440000000000 126 42 2016/2/29 2016/8/22 USDCNH--CNY 0.00010422100000000000 126 43 2018/12/3 2019/11/19 USDCNH--CNY 0.00011830200000000000 252 44 2013/4/1 2014/3/18 USDCNH--CNY 0.00015585000000000000 252 45 2013/5/27 2014/5/13 USDCNH--CNY 0.00015892200000000000 252 46 2011/9/19 2012/3/12 USDCNH--CNY 0.00019703300000000000 126 47 2010/12/13 2011/6/6 USDCNH--USDSGD 0.00024923700000000000 126 48 2016/10/10 2017/4/3 USDCNH--CNY 0.00029733300000000000 126 49 2019/3/25 2020/3/10 USDCNH--CNY 0.00034612000000000000 252 50 2018/10/8 2019/4/1 USDCNH--CNY 0.00054319400000000000 126
5. CNY-CNH协整分析
5.1 整体数据回归的残差直方图
通过下述代码，按年对CNY-CNY序列进行回归，提取残差序列后画出直方图及线图。
%matplotlib qt5
result_df=pd.DataFrame()
year_lst=sorted(set(pairs_df['Year'].to_list())) #把年份列先转成列表，然后通过集合去重，接着排序。用来循环画图
fig,ax=plt.subplots(len(year_lst),2,figsize=(13,20)) #准备好第一块画布和轴域，设置N行一列子图格式，用于按年画残差直方图
for i,year in enumerate(year_lst):
temp_range=pairs_df[pairs_df['Year']==year]
# print(f"{temp_range.index[0]}-------{temp_range.index[-1]} will be conducted OLS-regression: ") #如果对循环的逻辑有疑惑，可以开启本行调试语句
test_df=temp_range[['CNY','USDCNH','Year']]
cnh=test_df.USDCNH
cny=test_df.CNY
CNH=sm.add_constant(cnh)
temp_result=(sm.OLS(cny,CNH)).fit()
temp_residual_serial=cny-(temp_result.params.iloc[1])*cnh-(temp_result.params.iloc[0])
temp_residual_serial=sigma_filter(temp_residual_serial) #根据3倍方差为上下限，去除残差序列的极值
temp_mean=temp_residual_serial.mean()
temp_std=temp_residual_serial.std()
#用ADF方法，对残差序列的稳定性进行检验。如果返回p值小于1%临界值，则赋值ad_text，显示该序列通过ADF稳定性检验
ad_info=adfuller(temp_residual_serial)
if ad_info[0]<ad_info[4]['1%']:
ad_text=f"ADF test passed! t-value-{round(ad_info[0],3)} < 1%:-{round(ad_info[4]['1%'],3)}"
else:
ad_text="ADF test failed!"
ax[i,0].set_title(f'Year_{year}__Hist__Chart__{ad_text}') #将相关信息显示在第i张子图标题上，便于观察数据分布
temp_residual_serial.hist(ax=ax[i,0],bins=100,color="purple") #定为第i张子图左边格，在该子图中画出该年度的残差直方图
temp_residual_serial.plot(ax=ax[i,1],color="darkgreen") #定为第i张子图右边格，在该子图中画出该年度的残差线图
ax[i,1].axhline(temp_mean,color='black',linestyle="--")
ax[i,1].axhline(1.5*temp_std,color='red',linestyle="--")
ax[i,1].axhline(-1.5*temp_std,color='orange',linestyle="--")
cocat_df=pd.concat([temp_residual_serial,test_df['Year']],axis=1,keys=['residual','Year'])
result_df=pd.concat([result_df,cocat_df]) #将该年度的残差直方图拼接在数据框总表中
plt.tight_layout()
fig2,ax2=plt.subplots(2,1,figsize=(12,8)) #准备好第二块画布
result_df['residual'].hist(ax=ax2[0],bins=300,color='darkblue') #画出所有残差的直方图
temp_mean=result_df['residual'].mean()
temp_std=result_df['residual'].std()
ad_of_all_data=adfuller(result_df['residual'])
pvalue_all_data="pvalue"+str(ad_of_all_data[1])
result_df['residual'].plot(ax=ax2[1],color='darkgreen')
ax2[1].axhline(temp_mean,color='black',linestyle="--")
ax2[1].axhline(1.5*temp_std,color='red',linestyle="--")
ax2[1].axhline(-1.5*temp_std,color='orange',linestyle="--")
plt.text("2012",0.06,pvalue_all_data)在对USDCNY、USDCNH序列整体数据进行回归后，观察其残差序列的直方图及线图，可以看到其残差近似正态分布，无需对原始数据取对数获取对数收益序列再进行回归以缩小数据范围。对该残差序列的ADF检验得到的pvalue，显示该残差满足平稳性假设。
图5：2010-2022年整体残差直方图、线图
5.2 逐年回归的残差直方图
我们在逐年画出的残差直方图中，看到并不是每一年的残差序列都能满足稳定的假设。这意味着，并非每一年里面CNY-CNH的即期汇率序列都存在协整关系。2010年由于数据比较少，所以未能满足平稳性的假设。
满足平稳性假设的年份：【2013，2015，2016，2017，2018，2019，2020，2021，2022】；
未满足平稳性假设的年份：【2010，2011，2012，2014】
图6：逐年残差 zscore 直方图、线图
由图6得到的启示就是，自2015年至今，CNH-CNY的年度数据显示该货币对存在稳定的协整关系，通过协整关系来产生配对交易信号的策略大体可行。但是使用该信号进行USDCNY，USDCNH的配对交易时，需要注意协整关系遭到破坏时，价差无法向均值回归的策略风险。
结合4.5的滑动窗口寻优结果，协整关系自2015年以来，最优年份主要集中在2015年后---2020年前。其他的协整时段内，协整关系可信度不是太过理想。
这给我们的启示时： 如果如果2022年希望用配对交易策略的信号指导实际交易，可能需要把信号产生的上下界限稍微调宽。例如：2022年5月附近，我们可以看到误差多次向下突破1.0的位置。在此期间，zscore向均值回复时间较长。如果上下限区间的设定较窄，容易多次进出而高买低卖从而产生亏损，而多次进出也意味着手续费的浪费。当然，这是用了未来数据进行回测后得到的结论。实际交易中，只能通过其他的规则（止损/止盈等）设定，来降低该信号带来的亏损。
6. CNY-CNH配对策略交易代码
6.1 提取交易信号
在实际交易中，为了尽量避免未来数据对回测的干扰，我们会用过去250天的交易数据来拟合USDCNY 和USDCNH的协整关系。然后，我们会假设未来两周内，市场能大概率的运行在该拟合得出的对冲比率规律内。接着我们可以用该对冲比率计算未来的两周内USDCNY和USDCNH的残差序列。最后按照下述的信号设定规则来设置交易信号：
高偏信号-----zscore > 1.2-----交易操作：卖出USDCNY，买入USDCNH
低偏信号-----zscore < -1.2----交易操作：买入USDCNY，卖出USDCNH
def get_moving_coint_signal(df,start_day=251,train_length=250,project_days=10):
zscore_result=pd.DataFrame() #准备zscore_result数据框，用来接收并拼合在下述循环中产生的残差序列
hedge_ratio=pd.DataFrame() #准备hedge_ratio数据框，用来接收并拼合在下述循环中产生的对冲比率序列
while start_day+project_days < len(df):
train_df=df[(start_day-train_length):start_day] #根据每一个循环的时间区间，切片出拟合协整关系的训练数据集
cnh_train=train_df.USDCNH #获取CNH序列
cny_train=train_df.CNY #获取CNY序列
CNH_train=sm.add_constant(cnh_train) #为CNH序列添加常数序列
train_result=(sm.OLS(cny_train,CNH_train)).fit()
project_df = df[start_day:(start_day+project_days)] #根据每一个循环的时间区间，切片出预测数据集
cnh_project=project_df.USDCNH #获取预测数据集中的CNH序列
cny_project=project_df.CNY #获取预测数据集中的CNY序列
project_residual_serial=cny_project-(train_result.params.iloc[1])*cnh_project-(train_result.params.iloc[0]) #计算出预测数据集中的残差序列
project_residual_serial=sigma_filter(project_residual_serial) #根据3倍方差为上下限，修正残差序列的极值
zscore_project_residual=get_zscore(project_residual_serial) #对残差序列进行标准化
zscore_result=pd.concat([zscore_result,zscore_project_residual],axis=0) #把本次循环中处理好的标准化残差序列，拼接入总的残差结果数据框容器中
hedge_ratio_serial=pd.DataFrame(np.ones((project_days,1)) * train_result.params.iloc[1]) #把本次拟合的对冲比率，处理成一列常值序列，拼接到hedge_ratio的数据框容器中
hedge_ratio=pd.concat([hedge_ratio,hedge_ratio_serial],axis=0)
start_day += project_days #把时间窗口按照预设长度向前滑动，进行下一次循环计算
hedge_ratio=hedge_ratio.rename(columns={0:'hedge_ratio'})
hedge_ratio=hedge_ratio.set_index(df[251:(251+len(zscore_result))].index)
zscore_result=zscore_result.rename(columns={0:'residual'})
return zscore_result,hedge_ratio #返还装有计算结果的数据框6.2 计算回测收益并画图
计算收益时，我并没有使用对数收益的累加性质结合cumsum的方法。而是直接将两天内的价格差异算出来，然后用价差累加的方法来计算收益率。目测在计算有空仓信号的策略收益，这样计算收益率合理且更直观。
pair_trading_df=pairs_df[['USDCNH','CNY']] #获取即期价格数据集
zscore_result , hedge_ratio = get_moving_coint_signal(pair_trading_df,start_day=251,train_length=250,project_days=10) #设定两个数据框，接受信号计算函数计算出来残差序列和对冲比率序列
pair_trading_df=pair_trading_df.assign(cny_signal="",residual="",long_cny_return='',long_cnh_return='',pairs_trade_return='',hedge_ratio='') #向数据集数据框添加信息列
#设定1.2为信号触发阈值，装填残差序列，通过该残差序列计算交易信号
threshold=1.2
zscore_result=zscore_result[~zscore_result.index.duplicated()]
pair_trading_df['residual']=zscore_result['residual']
pair_trading_df['cny_signal']=np.where(pair_trading_df['residual']<-threshold,+1,np.where(pair_trading_df['residual']>threshold,-1,np.where((pair_trading_df['residual']<0.5)&(pair_trading_df['residual']>-0.5),0,"")))
hedge_ratio=hedge_ratio[~hedge_ratio.index.duplicated()]
pair_trading_df['hedge_ratio']=hedge_ratio['hedge_ratio'] #填入对冲比率序列
#根据交易信号的实际含义，用前值向后铺填。当检测到信号为+1，意味着买入该头寸。后续信号均为+1，意味着不对头寸进行新的买卖操作，持续持有该货币的多头寸，直至交易信号为0，也即对该头寸进行平仓操作。
#如果检测到信号为-1，意味着卖出该头寸。后续信号均为-1，意味着对该不做新的买卖操作。持续持有该货币的空头寸。直至交易信号为0，也即对该空头进行平补操作。
pair_trading_df['cny_signal'][pair_trading_df['cny_signal']==""]=np.nan
pair_trading_df['cny_signal']=pair_trading_df['cny_signal'].ffill()
pair_trading_df['cny_signal']=pair_trading_df['cny_signal'].astype("float")
#计算单独持有USDCNY的多头，每一天的累计收益率。
pair_trading_df.dropna(inplace=True)
pair_trading_df['long_cny_return']=(pair_trading_df['CNY'].diff(1).shift(-1)).cumsum()/ pair_trading_df['CNY'][0]
pair_trading_df['long_cny_return']=pair_trading_df['long_cny_return']*100
#计算单独持有USDCNH的多头，每一天的累计收益率。
pair_trading_df['long_cnh_return']=(pair_trading_df['USDCNH'].diff(1).shift(-1)).cumsum()/ pair_trading_df['USDCNH'][0]
pair_trading_df['long_cnh_return']=pair_trading_df['long_cnh_return']*100
#计算根据配对交易策略，按照交易信号，结合对冲比率计算配对交易的总体收益
pair_trading_df['pairs_trade_return']=(pair_trading_df['CNY'].diff(1).shift(-1)*pair_trading_df['cny_signal']).cumsum()/ pair_trading_df['CNY'][0] + (pair_trading_df['USDCNH'].diff(1).shift(-1)*(-pair_trading_df['cny_signal'])).cumsum()/ pair_trading_df['USDCNH'][0] * pair_trading_df['hedge_ratio']
pair_trading_df['pairs_trade_return']=pair_trading_df['pairs_trade_return']*100
#画出累计收益率走势图
fig4,ax4=plt.subplots(figsize=(15,10))
pair_trading_df['long_cny_return'].plot()
pair_trading_df['long_cnh_return'].plot()
pair_trading_df['pairs_trade_return'].plot()
ax4.axhline(pair_trading_df['long_cnh_return'][-2],linestyle='--')
ax4.legend()
plt.text("2022",200,round(pair_trading_df['pairs_trade_return'][-2],2))
plt.text("2022",8,round(pair_trading_df['long_cny_return'][-2],2))
图7：USDCNY-USDCNH配对收益走势图
7. 结语
从上面的收益走势图可以看到，自2010年开始，基于以一年期时间窗口来产生的交易信号来交易USDCNY--USDCNH的价差，收益200%，几何平均年化大概5.95%左右，比起BUY&HOLD 单个币种的收益增进不少。（此前用了算术平均的年化，虚高了年化收益为17%）
至于期间用哪个滑动时间窗口、选择多大的信号阈值、哪段时间内阈值需要调大还是调小,需要进一步的优化才能实现。同时本次练习的回测框架并未考虑手续费。实盘当中需要考虑更多技术细节。
还有一个相当重要的技术难点：对于不少外汇交易参与者来说，USDCNY--USDCNH的收益并不能很好的自由流转，从而能相互抵补构建该配对策略。对于此类参与者，可以用该信号来作为辅助交易信号。
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
