接着上文PCA的数学详细推导过程,本文介绍使用Python结合图像压缩案例解释PCA的具体实现流程,以了解数据处理的一些方法
Jupyter Notebook file
借助 scikit-learn 实现 PCA
使用scikit-learn库执行PCA过程,以对输入的数字图像数据进行降维。然后比较原始数据和重构数据之间的差异以熟悉过程。
输入数据
导入库,并可视化源输入数据。
# 导入所需的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.metrics import mean_squared_error
# 加载数字数据集
digits = load_digits()
X = digits.data
y = digits.target
# 计算原始数据大小
original_size = X.nbytes / (1024 * 1024) # in megabytes
print("original data size is: %.2f MB" % original_size)
original data size is: 0.88 MB
# 将前10个样本作为图像显示
fig, axes = plt.subplots(1, 10, figsize=(12, 4))
for i in range(10):
axes[i].imshow(X[i].reshape(8, 8), cmap='gray')
axes[i].set_title(f"Label: {y[i]}")
axes[i].axis('off')
plt.tight_layout()
plt.show()

PCA降维并重建
定义函数以计算重构误差和执行PCA
# Function to calculate reconstruction error
def reconstruction_error(original, reconstructed):
return mean_squared_error(original, reconstructed)
# 函数用于执行PCA并使用n_components重构数据。
def perform_pca(n_components):
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
X_reconstructed = pca.inverse_transform(X_pca)
return X_reconstructed, pca
# 执行PCA,并可视化结果
def analyze_pca(n_components):
X_reconstructed, pca = perform_pca(n_components)
reconstruction_error_val = reconstruction_error(X, X_reconstructed)
print(f"Number of Components: {n_components}, Reconstruction Error: {reconstruction_error_val}")
# 压缩文件的大小
compressed_size = (pca.components_.nbytes + pca.mean_.nbytes + X_reconstructed.nbytes) / (1024 * 1024) # in megabytes
print(f"Size of Compressed File: {compressed_size} MB")
# 大小差异
size_difference = original_size - compressed_size
print(f"Difference in Size: {size_difference} MB")
# 绘制每个数字的原始和重构图像
fig, axes = plt.subplots(2, 10, figsize=(10, 2))
for digit in range(10):
digit_indices = np.where(y == digit)[0] # Indices of samples with the current digit
original_matrix = X[digit_indices[0]].reshape(8, 8) # Take the first sample for each digit
reconstructed_matrix = np.round(X_reconstructed[digit_indices[0]].reshape(8, 8), 1) # Round to one decimal place
axes[0, digit].imshow(original_matrix, cmap='gray')
axes[0, digit].axis('off')
axes[1, digit].imshow(reconstructed_matrix, cmap='gray')
axes[1, digit].axis('off')
plt.suptitle(f'Reconstruction with {n_components} Components')
plt.show()
# 打印第一个数据的原始矩阵
print("Original Matrix of the First Data:")
print(original_matrix)
# 打印重构矩阵
print("\nReconstruction Matrix of the First Data:")
print(reconstructed_matrix)
分析当使用一个主成分PCA时的重建结果
analyze_pca(1)
Number of Components: 1, Reconstruction Error: 15.977678462238496
Size of Compressed File: 0.87841796875 MB
Difference in Size: -0.0009765625 MB

Original Matrix of the First Data:
[[ 0. 0. 11. 12. 0. 0. 0. 0.]
[ 0. 2. 16. 16. 16. 13. 0. 0.]
[ 0. 3. 16. 12. 10. 14. 0. 0.]
[ 0. 1. 16. 1. 12. 15. 0. 0.]
[ 0. 0. 13. 16. 9. 15. 2. 0.]
[ 0. 0. 0. 3. 0. 9. 11. 0.]
[ 0. 0. 0. 0. 9. 15. 4. 0.]
[ 0. 0. 9. 12. 13. 3. 0. 0.]]
Reconstruction Matrix of the First Data:
[[-0. 0.4 6.4 12.6 12. 6.3 1.4 0.1]
[ 0. 2.6 11.7 11.2 10.5 9.4 1.9 0.1]
[ 0. 3. 9.4 5.8 8. 8.7 1.6 0. ]
[ 0. 2.1 7.7 9. 11.1 7.8 2. 0. ]
[ 0. 1.5 5.6 8.2 9.8 8.5 2.8 0. ]
[ 0. 1. 5.2 5.9 6.5 8.2 3.7 0. ]
[ 0. 0.8 7.8 9. 8.8 9.5 4.1 0.2]
[ 0. 0.4 6.8 12.9 11.9 7.3 2.3 0.4]]
分析当使用5个主成分PCA时的结果
analyze_pca(5)
Number of Components: 5, Reconstruction Error: 8.542447616249266
Size of Compressed File: 0.88037109375 MB
Difference in Size: -0.0029296875 MB

Original Matrix of the First Data:
[[ 0. 0. 11. 12. 0. 0. 0. 0.]
[ 0. 2. 16. 16. 16. 13. 0. 0.]
[ 0. 3. 16. 12. 10. 14. 0. 0.]
[ 0. 1. 16. 1. 12. 15. 0. 0.]
[ 0. 0. 13. 16. 9. 15. 2. 0.]
[ 0. 0. 0. 3. 0. 9. 11. 0.]
[ 0. 0. 0. 0. 9. 15. 4. 0.]
[ 0. 0. 9. 12. 13. 3. 0. 0.]]
Reconstruction Matrix of the First Data:
[[ 0. 0.2 5.2 11.1 12.1 7. 1.6 0.1]
[ 0. 2.1 11.2 10.7 9.7 9.6 2.3 0.2]
[ 0. 3.1 11.2 6.2 6. 9.2 2.5 0.1]
[ 0. 3.1 10.3 9. 9.6 9.6 2.9 0. ]
[ 0. 2.2 6. 5.3 8. 11.6 3.9 0. ]
[ 0. 1.2 4.2 1.9 4.9 11.7 5.1 0. ]
[ 0. 0.6 6.7 6.2 8.8 12.1 4.4 0.2]
[ 0. 0.2 5.4 12.1 13.4 8.2 1.8 0.3]]
一个明显的效果是使用更多的主成分,重构结果会更好。接下来手动计算PCA矩阵,了解其详细工作原理。
手动实现 PCA 过程
手动逐步执行PCA分析。
输入数据
导入数据并打印数据矩阵与图像
# 然后使用逐步的方法计算PCA步骤;
# 取第一个数据点进行分析
first_data = X[0]
print("Raw input data: \n", X[0])
# 将数据点重新整形为二维数组(图像)
input_matrix = first_data.reshape(8, 8)
print("Input matrix: ")
for row in input_matrix:
print(" ".join(f"{val:4.0f}" for val in row))
# 打印原始矩阵(图像)
plt.imshow(input_matrix, cmap='gray')
plt.title("Input matrix (Image)")
plt.axis('off')
plt.show()
Raw input data:
[ 0. 0. 5. 13. 9. 1. 0. 0. 0. 0. 13. 15. 10. 15. 5. 0. 0. 3.
15. 2. 0. 11. 8. 0. 0. 4. 12. 0. 0. 8. 8. 0. 0. 5. 8. 0.
0. 9. 8. 0. 0. 4. 11. 0. 1. 12. 7. 0. 0. 2. 14. 5. 10. 12.
0. 0. 0. 0. 6. 13. 10. 0. 0. 0.]
Raw data shape: (64,)
Input matrix:
0 0 5 13 9 1 0 0
0 0 13 15 10 15 5 0
0 3 15 2 0 11 8 0
0 4 12 0 0 8 8 0
0 5 8 0 0 9 8 0
0 4 11 0 1 12 7 0
0 2 14 5 10 12 0 0
0 0 6 13 10 0 0 0

数据居中处理
居中数据是PCA中的关键预处理步骤,它增强了结果的解释性,消除了偏差,并确保了计算中的数值稳定性。
均值计算有助于我们理解每个特征的平均值,这对于居中数据和在随后的步骤中计算协方差矩阵至关重要。
# 步骤1:计算每个特征(列)的均值
mean_vec = np.mean(input_matrix, axis=0)
print(mean_vec)
[ 0. 2.25 10.5 6. 5. 8.5 4.5 0. ]
# 步骤2:从每个特征中减去均值
centered_matrix = input_matrix - mean_vec
print(centered_matrix)
[[ 0. -2.25 -5.5 7. 4. -7.5 -4.5 0. ]
[ 0. -2.25 2.5 9. 5. 6.5 0.5 0. ]
[ 0. 0.75 4.5 -4. -5. 2.5 3.5 0. ]
[ 0. 1.75 1.5 -6. -5. -0.5 3.5 0. ]
[ 0. 2.75 -2.5 -6. -5. 0.5 3.5 0. ]
[ 0. 1.75 0.5 -6. -4. 3.5 2.5 0. ]
[ 0. -0.25 3.5 -1. 5. 3.5 -4.5 0. ]
[ 0. -2.25 -4.5 7. 5. -8.5 -4.5 0. ]]
协方差矩阵计算
计算居中处理后数据的协方差矩阵。
# 使用np.dot计算协方差。Bessel修正在末尾减1。 https://www.uio.no/studier/emner/matnat/math/MAT4010/data/forelesningsnotater/bessel-s-correction---wikipedia.pdf
cov_matrix = np.dot(centered_matrix.T, centered_matrix) / (centered_matrix.shape[0] - 1)
# 或者使用np.cov计算协方差
# cov_matrix = np.cov(centered_matrix, rowvar=False)
print(cov_matrix)
[[ 0. 0. 0. 0. 0.
0. 0. 0. ]
[ 0. 4.21428571 2.28571429 -13.14285714 -9.42857143
4.14285714 6.14285714 0. ]
[ 0. 2.28571429 14. -9.42857143 -4.85714286
17. 6.28571429 0. ]
[ 0. -13.14285714 -9.42857143 43.42857143 29.57142857
-12.57142857 -17.85714286 0. ]
[ 0. -9.42857143 -4.85714286 29.57142857 26.
-7. -17.57142857 0. ]
[ 0. 4.14285714 17. -12.57142857 -7.
28.85714286 11. 0. ]
[ 0. 6.14285714 6.28571429 -17.85714286 -17.57142857
11. 14.85714286 0. ]
[ 0. 0. 0. 0. 0.
0. 0. 0. ]]
矩阵的特征分解
# 计算协方差矩阵的特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
print(eigenvalues)
print(eigenvectors)
[8.92158455e+01 3.14545089e+01 7.61850164e+00 2.85144338e+00
2.01453633e-01 1.53898738e-02 0.00000000e+00 0.00000000e+00]
[[ 0. 0. 0. 0. 0. 0.
1. 0. ]
[-0.20365153 0.09344175 0.07506402 -0.23052329 -0.41043409 -0.85003703
0. 0. ]
[-0.22550077 -0.48188982 0.20855091 0.79993174 -0.1168451 -0.14104805
0. 0. ]
[ 0.65318552 -0.28875672 -0.59464342 0.12374602 0.11324705 -0.32898247
0. 0. ]
[ 0.48997693 -0.31860576 0.39448425 -0.20610464 -0.63307453 0.24399318
0. 0. ]
[-0.33563583 -0.75773097 -0.0607778 -0.49775699 0.24837474 0.00681139
0. 0. ]
[-0.35818338 -0.00212894 -0.66178497 0.03760326 -0.58531429 0.29955628
0. 0. ]
[ 0. 0. 0. 0. 0. 0.
0. 1. ]]
选择与最大特征值对应的特征向量作为主成分。
# 选择与最大特征值对应的主成分
max_eigenvalue_index = np.argmax(eigenvalues)
principal_component = eigenvectors[:, max_eigenvalue_index]
print(principal_component)
[ 0. -0.20365153 -0.22550077 0.65318552 0.48997693 -0.33563583
-0.35818338 0. ]
# 将数据投影到主成分上
reduced_data = np.dot(centered_matrix, principal_component)
# 打印降维后的数据
print("Reduced data (1 principal component):\n", reduced_data)
Reduced data (1 principal component):
[12.35977044 5.86229378 -8.32285024 -8.14946302 -7.7867473 -8.41834525
1.49545914 12.95988243]
到目前为止,数据已从原来的 8x8 矩阵压缩为 8x1 的向量,接下来看一下使用降维后数据重建的效果。
重构数据
现在基于降维后的结果来重新组建原数据,并展示效果。
# 步骤7:重构数据
reconstructed_data = np.dot(reduced_data.reshape(-1, 1), principal_component.reshape(1, -1))
# 步骤8:将均值添加回重构的数据
reconstructed_data += mean_vec
# 步骤9:可视化原始数据和重构数据
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 原始数据
axes[0].imshow(input_matrix, cmap='gray')
axes[0].set_title('Original Data')
axes[0].axis('off')
# Reconstructed data
axes[1].imshow(reconstructed_data.real, cmap='gray')
axes[1].set_title('Reconstructed Data')
axes[1].axis('off')
plt.show()
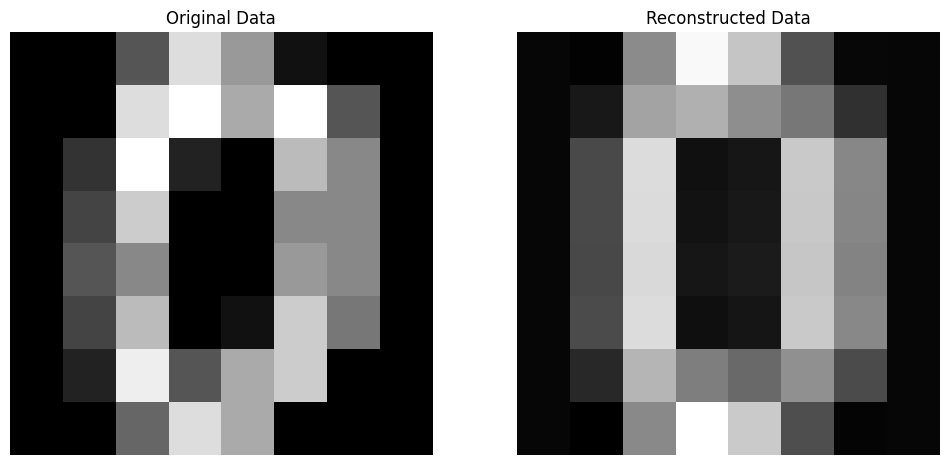
对比上图,发现重建数据清晰程度仍然不错,与输入图像有些许差别但是主要的特征都可以清晰分辨。






















 1170
1170











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










