【最短路径算法】之 Dijkstra 算法：附Java示例代码

码到π退休

已于 2024-08-28 22:30:26 修改

阅读量2.5k

点赞数 47

分类专栏：算法和数据结构文章标签：算法 Dijkstra算法

于 2024-08-27 00:15:00 首次发布

本文链接：https://blog.csdn.net/lilinhai548/article/details/141527598

版权

算法和数据结构专栏收录该内容

3 篇文章

订阅专栏

1. 前言

卫星导航系统如何在最短的时间内找到从起点到终点的最短路线？这个（和类似的）问题将在本系列关于“最短路径”算法的文章中得到解决。

本部分介绍 Dijkstra 算法 - 以其发明者艾兹格·W·迪科斯彻（Edsger W. Dijkstra）的名字命名。Dijkstra 算法针对图中给定的起始节点，找到到所有其他节点（或到给定的目标节点）的最短距离。

2. Dijkstra 算法 – 示例

用一个例子来解释 Dijkstra 算法是最好的。下图显示了一张虚构的道路地图。带有字母的圆圈代表地点；线条是连接这些地点的道路和路径。

路线图

粗线代表高速公路；稍细的线是乡村道路，虚线则是难以通行的土路。

现在我们将路线图绘制成图表。村庄成为节点，道路和小路成为边。

边的权重表示从一个地方到另一个地方需要多少分钟。路径的长度和性质都起着作用，即一条长的高速公路可能比一条短得多的土路通行更快。

图表结果如下：

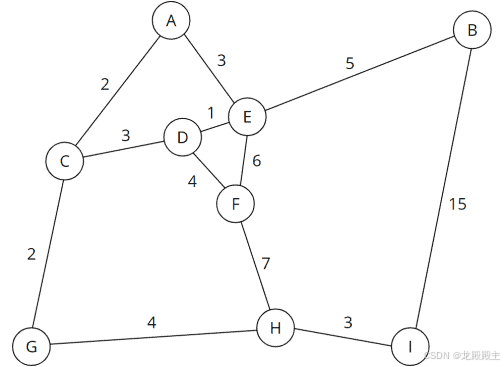
加权图形式的路线图

例如，从图中可以看出，从 D 到 H 的路线在最短路线上需要 11 分钟，即通过节点 F 的土路（路线以黄色突出显示）。在通过节点 C 和 G 的乡村道路和高速公路的明显较长的路线上（蓝色路线），仅需 9 分钟：

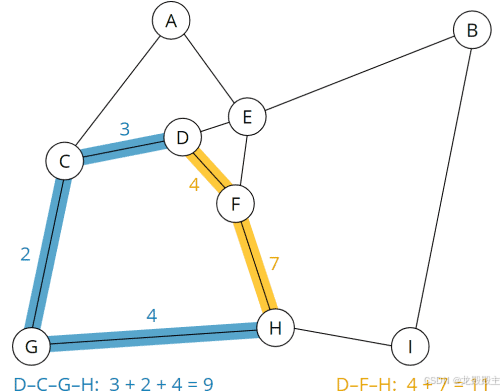
最快和最短路径

人类大脑非常擅长识别此类模式。然而，必须先通过适当的方法教会计算机识别此类模式。这就是 Dijkstra 算法发挥作用的地方。

2.1 准备 – 节点表

我们首先要做一些准备：我们创建一个节点表，其中包含两个附加属性：前任节点和到起始节点的总距离。前任节点最初保持为空；起始节点的总距离在起始节点本身中设置为 0，在所有其他节点中设置为 ∞（无穷大）。

该表按到起始节点的总距离按升序排序，即起始节点本身（节点 D）位于表的顶部；其他节点未排序。在示例中，我们按字母顺序排列它们：

节点	前任	总距离
D	–	0
A	–	∞
B	–	∞
C	–	∞
E	–	∞
F	–	∞
G	–	∞
H	–	∞
I	–	∞

在以下章节中，区分距离和总距离这两个术语非常重要：

距离：一个节点到其相邻节点的距离；
总距离：从起始节点经由可能的中间节点到特定节点的所有部分距离的总和。

2.2 Dijkstra 算法分步指南 – 处理节点

在以下图表中，还显示了节点的前身和总距离。这些数据通常不包含在图表本身中，而只包含在上文所述的表格中。我在这里显示它以方便理解。

2.2.1 步骤 1：查看起点的所有邻居

现在我们从列表中删除第一个元素 - 节点 D - 并检查它的邻居，即 C，E 和 F。

从 D 可达的节点

由于所有这些邻居中的总距离仍然是无限的（即，我们还没有发现到达那里的路径），我们将邻居的总距离设置为从 D 到相应邻居的距离，并将 D 设置为每个邻居的前任。

更新了节点 C、E、F 的总距离和前任

我们再次按总距离对列表进行排序（更改的条目以粗体突出显示）：

节点	前任	总距离
E	D	1
C	D	3
F	D	4
A	–	∞
B	–	∞
G	–	∞
H	–	∞
I	–	∞

该列表应如下所示：发现节点 E、C 和 F，并可分别在 1、3 和 4 分钟内通过 D 到达。

2.2.2 步骤 2：检查节点 E 的所有邻居

对于列表的下一个节点（节点 E），我们重复刚刚对起始节点 D 所做的事情。我们取 E 并查看其邻居 A、B、D 和 F：

从 E 可达的节点

对于节点 A 和 B 来说，总距离仍然是无限的。因此我们将它们的总距离设置为当前节点 E 的总距离（即 1）加上从 E 到各自节点的距离：

节点A	1 （到 E 的最短总距离） + 3 （距离 E - A） = 4
节点 B	1 （到 E 的最短总距离） + 5 （距离 E - B） = 6

节点 D 不再包含在表中。这意味着已经发现了到它的最短路径（它是起始节点）。因此我们不需要进一步查看该节点。

以下图表再次更新了 A 和 B 的条目：

更新了节点 A、B 的总距离和前任

到节点 F 的总距离已经填写（经节点 D 到达 4）。为了检查是否可以通过当前节点 E 更快地到达 F，我们计算经 E 到达 F 的总距离：

节点 F	1 （到 E 的最短总距离） + 6 （E-F 距离） = 7

我们将此总距离与为 F 设置的总距离进行比较。重新计算的总距离 7 大于存储的总距离 4。因此，经由 E 的路径比之前检测到的路径更长。因此，我们不再关注它，并且我们保持 F 的表条目不变。

这导致表中的状态如下（更改以粗体突出显示）：

节点	前任	总距离
C	D	3
F	D	4
A	E	4
B	E	6
G	–	∞
H	–	∞
I	–	∞

新的条目应该这样读：A 和 B 被发现；总共需要 4 分钟可以通过节点 E 到达 A，总共需要 6 分钟可以通过节点 E 到达 B。

2.2.3 步骤 3：检查节点 C 的所有邻居

我们对列表中的下一个节点重复该过程：节点 C。我们将其从列表中删除，并查看其邻居 A、D 和 G：

从 C 可达的节点

节点 D 已从列表中删除并被忽略。

我们计算从 C 到 A 和 G 的总距离：

节点A	3 （到 C 的最短总距离） + 2 （距离 C - A） = 5
节点G	3 （到 C 的最短总距离） + 2 （距离 C - G） = 5

对于 A，已经存储了一条经由 E 的较短路径，总距离为 4。因此，我们忽略了新发现的经由 C 到 A 的总距离更大的路径 5，并保持 A 的表项不变。

节点 G 的总距离仍为无穷大。因此，我们输入 G 经过前任节点 C 的总距离为 5：

更新了节点 G 的总距离和前任

G 现在的总距离比 B 短，因此在表中上升一个位置：

节点	前任	总距离
F	D	4
A	E	4
G	C	5
B	E	6
H	–	∞
I	–	∞

2.2.4 步骤 4：检查节点 F 的所有邻居

我们从列表中删除下一个节点，即节点 F，并查看它的邻居 D、E 和 H：

从 F 可达的节点

到节点 D 和 E 的最短路径已经被发现；因此我们只需要计算通过当前节点 F 到 H 的总距离：

节点 H	4 （到 F 的最短总距离） + 7 （距离 F - H） = 11

节点 H 的总距离仍然无限大；因此，我们将当前节点 F 设置为前任，并将 11 设置为总距离：

更新了节点 H 的总距离和前任

H 是我们的目标节点。因此，我们找到了一条通往目的地的路线，总距离为 11。但我们还不知道这是否是最短的路径。表中还有三个节点的总距离小于 11：A、G 和 B：

节点	前任	总距离
A	E	4
G	C	5
B	E	6
H	F	11
I	–	∞

也许从其中一个节点到目的地还有另一条短路径，总距离可以小于 11。

因此我们必须继续这个过程，直到目标节点 H 之前的表中没有任何条目。

2.2.5 步骤 5：检查节点 A 的所有邻居

我们移除节点 A，并查看其邻居 C 和 E：

从 A 可达的节点

这两个节点都不再包含在表中，因此这两个节点的最短路径都已发现 - 因此我们可以忽略它们。这意味着没有办法通过节点 A 到达目的地。第 6 步到此结束。

2.2.6 步骤 6：检查节点 G 的所有邻居

我们删除节点 G 并检查其邻居 C 和 H：

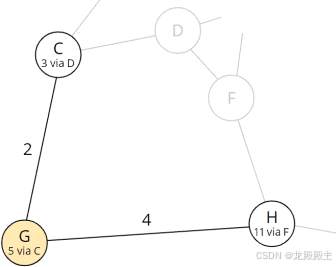
从 G 可达的节点

C 已经处理完毕；剩下的就是计算经由 G 到节点 H 的总距离：

节点 H	5 （到 G 的最短总距离） + 4 （距离 G - H） = 9

节点 H 目前经过节点 F 的总距离为 11。在步骤 5 中，我们找到了相应的路径。现在，总距离为 9，我们找到了一条更短的路线！因此，我们将 H 中的 11 替换为 9，将前任 F 替换为当前节点 G：

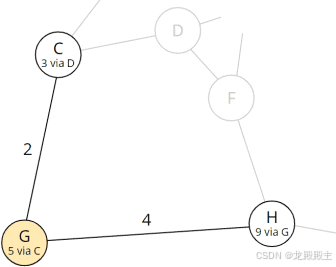
该表现在如下所示：

节点	前任	总距离
B	E	6
H	G	9
I	–	∞

通过节点 B，我们可以找到一条到达目的地的更短路径，所以我们必须最后看这条路径。

2.2.7 步骤 7：检查节点 B 的所有邻居

因此我们移除节点 B 并查看其邻居 E 和 I：

从 B 可达的节点

对于 E，我们已经发现了最短路径；对于 I，我们计算了 B 上的总距离：

节点一	6 （到 B 的最短总距离） + 15 （距离 B - I） = 21

对于节点 I，我们将计算出的总距离和当前节点存储为前任：

节点 I 的总距离和前任已更新

表中，I 位于 H 之后：

节点	前任	总距离
H	G	9
I	B	21

2.2.8 找到到达目的地的最短路径

列表中的第一个条目现在是我们的目标节点 H。不再有总距离更短的未被发现的节点，以便我们能够找到更短的路径。

从表中我们可以得知：到达目标节点H的最短路径是通过G，总距离为9。

2.3 回溯——确定完整路径

但如何确定从起始节点D到目标节点H的完整路径呢？要做到这一点，我们必须一步步地遵循前人的经验。

我们使用表中存储的前任节点执行所谓的“回溯”。为了清楚起见，我在图中再次显示了这些数据：

用于确定完整路径的回溯

目的节点H的前身为G，G的前身为C，C的前身为起点D。所以最短路径为：D–C–G–H。

2.4 查找所有节点的最短路径

如果我们此时不终止算法，而是继续下去，直到表只包含一个条目，我们就找到了所有节点的最短路径！

在示例中，我们只需要查看节点 H – G 和 I 的邻居节点：

从 H 可达的节点

节点 G 已经被处理；我们计算经由 H 到 I 的总距离：

节点一	9 （到 H 的最短总距离） + 3 （距离 H - I） = 12

新计算出的到 I 的路线（经 H 到达 12）比已存储的路线（经 B 到达 21）短。因此，我们在节点 I 中替换前任和总距离：

节点 I 的总距离和前任已更新

该表现在仅包含节点 I：

节点	前任	总距离
I	B	12

如果我们现在删除节点I，则表为空，即已经找到了到I的所有相邻节点的最短路径。

因此，我们找到了图中所有节点从起始节点 D 出发（或到起始节点 D ）的最短路线！

3. Dijkstra 最短路径算法 – 非正式描述

准备：

创建一个包含所有节点及其前任和总距离的表。
将起始节点的总距离设置为 0，并将所有其他节点的总距离设置为无穷大。

处理节点：

只要表不为空，就取总距离最小的元素并执行以下操作：

提取出的元素是否为目标节点？如果是，则满足终止条件。然后顺着前驱节点回到起始节点，确定最短路径。
否则，检查所提取元素的所有相邻节点（这些节点仍在表中）。对于每个邻居节点：
1. 将总距离计算为提取节点的总距离加上到检查邻居节点的距离之和。
2. 如果该总距离比之前存储的总距离短，则将邻近节点的前任设置为被移除的节点，并将总距离设置为新计算的距离。

4. Dijkstra 算法 – 带有 PriorityQueue 的 Java 源代码

如何用 Java 最好地实现 Dijkstra 算法？

下面，我将逐步向您展示源代码。您可以在我的GitHub 存储库中找到完整的代码。各个类的链接也在下面。

4.1 图的数据结构：Guava ValueGraph

首先，我们需要一个存储图的数据结构，即节点、连接节点的边及其权重。

为此，一个合适的类是Google Core Libraries for Java中的ValueGraph 。此处解释了库提供的不同类型的图表。

我们可以创建一个类似于上面示例的 ValueGraph，如下所示（GitHub 存储库中的TestWithSampleGraph类）：

private static ValueGraph<String, Integer> createSampleGraph() {
   MutableValueGraph<String, Integer> graph = ValueGraphBuilder.undirected().build();
   graph.putEdgeValue("A", "C", 2);
   graph.putEdgeValue("A", "E", 3);
   graph.putEdgeValue("B", "E", 5);
   graph.putEdgeValue("B", "I", 15);
   graph.putEdgeValue("C", "D", 3);
   graph.putEdgeValue("C", "G", 2);
   graph.putEdgeValue("D", "E", 1);
   graph.putEdgeValue("D", "F", 4);
   graph.putEdgeValue("E", "F", 6);
   graph.putEdgeValue("F", "H", 7);
   graph.putEdgeValue("G", "H", 4);
   graph.putEdgeValue("H", "I", 3);
   return graph;
 }

的类型参数ValueGraph为：

节点类型：在我们的例子中，String节点名称为“A”至“I”
边值的类型：在我们的例子中，Integer表示节点之间的距离

由于图是无向的，因此指定节点的顺序并不重要。

4.2 数据结构：节点、总距离和前任

除了图表之外，我们还需要一个数据结构来存储节点以及与起点和前导节点之间的相应总距离。为此，我们创建了以下内容NodeWrapper（GitHub 存储库中的类）。类型变量N是节点的类型——在我们的示例中，它将用于String节点名称。

class NodeWrapper<N> implements Comparable<NodeWrapper<N>> {
  private final N node;
  private int totalDistance;
  private NodeWrapper<N> predecessor;

  NodeWrapper(N node, int totalDistance, NodeWrapper<N> predecessor) {
    this.node = node;
    this.totalDistance = totalDistance;
    this.predecessor = predecessor;
  }

  // getter for node
  // getters and setters for totalDistance and predecessor

  @Override
  public int compareTo(NodeWrapper<N> o) {
    return Integer.compare(this.totalDistance, o.totalDistance);
  }

  // equals(), hashCode()
}

NodeWrapper实现Comparable
接口：使用该compareTo()方法，我们定义自然顺序，以便NodeWrapper对象根据它们的总距离按升序排序。

以下部分中显示的代码构成了该类（GitHub 中的类findShortestPath()）的方法。DijkstraWithPriorityQueue

4.3 数据结构：PriorityQueue 作为表

此外，我们需要一个表的数据结构。

PriorityQueue通常用于此目的。始终将最小元素保留在其头部，我们可以使用方法检索该元素。对象的自然顺序稍后将确保始终返回总距离最小的元素。PriorityQueuepoll()NodeWrapperpoll()NodeWrapper

事实上，aPriorityQueue并不是最佳的数据结构。不过，我暂时会使用它。在后面的“使用 PriorityQueue 的运行时”部分中，我将测量实现的性能，然后解释为什么会PriorityQueue导致性能不佳——最后展示一个更合适的数据结构，其性能要好几个数量级。

PriorityQueue<NodeWrapper<N>> queue = new PriorityQueue<>();

4.4 数据结构：NodeWrapper 的查找图

NodeWrapper我们还需要一个映射来为我们提供图中节点的对应关系。AHashMap最适合这种情况：

Map<N, NodeWrapper<N>> nodeWrappers = new HashMap<>();

4.5 数据结构：完成的节点

我们需要能够检查我们是否已经完成了一个节点，即我们是否已经找到了到该节点的最短路径。AHashSet适合于此：

Set<N> shortestPathFound = new HashSet<>();

4.6 准备：填满桌子

让我们进入算法的第一步，即填充表格。

这里我们立即进行了一些优化。我们不需要将所有节点都写入表中——起始节点就足够了。我们只在找到通向其他节点的路径时才将其写入表中。

这种方法有两个优点：

我们保存那些从起点根本无法到达的节点的表条目，或者只能通过距离起点比距离目的地更远的中间节点到达的节点。
当我们稍后计算节点的总距离时，该节点不会自动在中重新排序PriorityQueue。相反，我们必须删除该节点并再次插入。由于对于所有发现的节点，总距离将小于无穷大，因此我们必须从队列中删除所有节点并再次插入它们。我们也可以通过在准备阶段根本不插入节点来节省这一时间。

因此，我们首先将起始节点包装成一个NodeWrapper对象（总距离为 0 且没有前任），然后将其插入到查找图和表中：

NodeWrapper<N> sourceWrapper = new NodeWrapper<>(source, 0, <strong>null</strong>);
nodeWrappers.put(source, sourceWrapper);
queue.add(sourceWrapper);

迭代所有节点

让我们进入算法的核心：对表（或者我们选择作为表的数据结构的队列）的逐步处理：

while (!queue.isEmpty()) {
  NodeWrapper<N> nodeWrapper = queue.poll();
  N node = nodeWrapper.getNode();
  shortestPathFound.add(node);

  // Have we reached the target? --> Build and return the path
  if (node.equals(target)) {
    return buildPath(nodeWrapper);
  }

  // Iterate over all neighbors
  Set<N> neighbors = graph.adjacentNodes(node);
  for (N neighbor : neighbors) {
    // Ignore neighbor if shortest path already found
    if (shortestPathFound.contains(neighbor)) {
      continue;
    }

    // Calculate total distance to neighbor via current node
    int distance =
        graph.edgeValue(node, neighbor).orElseThrow(IllegalStateException::new);
    int totalDistance = nodeWrapper.getTotalDistance() + distance;

    // Neighbor not yet discovered?
    NodeWrapper<N> neighborWrapper = nodeWrappers.get(neighbor);
    if (neighborWrapper == <strong>null</strong>) {
      neighborWrapper = new NodeWrapper<>(neighbor, totalDistance, nodeWrapper);
      nodeWrappers.put(neighbor, neighborWrapper);
      queue.add(neighborWrapper);
    }

    // Neighbor discovered, but total distance via current node is shorter?
    // --> Update total distance and predecessor
    else if (totalDistance < neighborWrapper.getTotalDistance()) {
      neighborWrapper.setTotalDistance(totalDistance);
      neighborWrapper.setPredecessor(nodeWrapper);

      // The position in the PriorityQueue won't change automatically;
      // we have to remove and reinsert the node
      queue.remove(neighborWrapper);
      queue.add(neighborWrapper);
    }
  }
}

// All reachable nodes were visited but the target was not found
return <strong>null</strong>;

由于有了评论，该代码就不需要进一步解释了。

4.7 回溯：确定从起点到终点的路线

如果从队列中取出的节点是目标节点（上面循环中的“我们到达目标了吗？”while块），buildPath()则调用该方法。它沿着前导节点从目标节点向后追溯到起始节点的路径，将节点写入列表，然后以相反的顺序返回它们：

private static <N> List<N> buildPath(NodeWrapper<N> nodeWrapper) {
  List<N> path = new ArrayList<>();
  while (nodeWrapper != <strong>null</strong>) {
    path.add(nodeWrapper.getNode());
    nodeWrapper = nodeWrapper.getPredecessor();
  }
  Collections.reverse(path);
  return path;
}

完整方法可以在GitHub 存储库中的 DijkstraWithPriorityQueue 类findShortestPath()中找到。您可以像这样调用该方法：

ValueGraph<String, Integer> graph = createSampleGraph();
List<String> shortestPath = DijsktraWithPriorityQueue.findShortestPath(graph, "D", "H");

我已createSampleGraph()在本章开头展示了该方法。

接下来我们来讨论时间复杂度。

5. Dijkstra 算法的时间复杂度

为了确定算法的时间复杂度
，我们逐块查看代码。下面，我们用m表示边数，用n表示节点数。

将起始节点插入表中：复杂度与图的大小无关，因此它是常数：O(1)。
从表中删除节点：每个节点最多从表中删除一次。此操作所需的工作量取决于所使用的数据结构；我们将其称为T em（“提取最小值”）。因此，所有节点的工作量为O(n · T em )。
检查是否已找到通向节点的最短路径：对每个节点以及从该节点引出的所有边执行此检查。由于每条边都连接到两个节点，因此每条边执行两次，即2m次。由于我们使用集合进行检查，因此此操作在常数时间内完成；对于2m 个节点，总工作量为O(m)。
计算总距离：每条边最多计算一次总距离，因为我们每条边最多找到一次到达节点的新路线。计算本身需要不断努力，因此此步骤的总工作量也是O(m)。
访问 NodeWrappers：这也是需要不断努力的，每个边最多访问一次；因此，这里也有O(m) 。
插入表：每个节点最多插入队列一次。插入的工作量取决于所使用的数据结构。我们将其称为T i（“插入”）。因此，所有节点的总工作量为O(n · T i )。
更新表中的总距离：对于每条边，此操作最多发生一次；与计算总距离的原理相同。我们在源代码中通过移除并重新插入解决了这个问题。但是，也有一些数据结构可以在一个步骤中最佳地完成此操作。因此，我们通常将此工作称为T dk（“减少密钥”）。对于m条边，因此为O(m · T dk )。

如果我们把所有的点加起来，我们得出：

O(1) + O(n·T em ) + O(m) + O(m) + O(m) + O(n·T i ) + O(m·T dk )

我们可以忽略恒定的努力O(1)；同样，与O(m · T dk )相比，O(m)变得可以忽略不计。因此，该术语缩短为：

O(n · (T em +T i ) + m · T dk )

您将在以下章节中了解T em、T i、T dk的值对于PriorityQueue和其他数据结构意味着什么——以及这对整体复杂性意味着什么。

5.1 具有 PriorityQueue 的 Dijkstra 算法

以下值可从类文档中获取，适用于 Java PriorityQueue。（为了便于理解，我在这里提供了T参数及其完整符号。）

删除最小条目poll()：T extractMinimum = O(log n)
插入条目offer()：T insert = O(log n)
remove()使用和更新总距离offer()：T declineKey = O(n) + O(log n) = O(n)

如果我们将这些值放入上面的公式中 – T em +T i = log n + log n可以合并为单个log n – 那么我们得到：

O(n· logn + m·n)

对于特殊情况，即边数是节点数的倍数——用大 O 表示：m ∈ O(n) ——考虑到时间复杂度， m和n可以相等。然后公式简化为O(n · log n + n²)。除了二次部分外，拟线性部分可以忽略，剩下的是：

O（n²） ——对于m ∈ O（n）

理论已经讲得足够多了……在下一节中，我们将在实践中验证我们的假设！

5.2 使用 PriorityQueue 运行时

为了检查理论上确定的时间复杂度是否正确，我编写了程序TestDijkstraRuntime。该程序创建大小从 10,000 到大约 300,000 个节点不等的随机图，并搜索两个随机选择的节点之间的最短路径。

每个图的边数是节点数的四倍。这类似于公路地图，平均每个路口有大约四条路通向其他路口。

每个测试重复 50 次；下图显示了与图表大小相关的测量时间中值：

使用 PriorityQueue 的 Dijkstra 算法的时间复杂度

您可以非常清楚地看到预测的二次增长 - 因此我们推导的O（n²）的时间复杂度是正确的。

5.3 使用 TreeSet 的 Dijkstra 算法

在确定时间复杂度时，我们认识到该PriorityQueue.remove()方法的时间复杂度为O(n)。这导致整个算法的时间复杂度为二次方。

更合适的数据结构是TreeSet。这提供了pollFirst()提取最小元素的方法。根据文档，以下运行时适用于TreeSet：

删除最小条目pollFirst()：T extractMinimum = O(log n)
插入条目add()：T insert = O(log n)
remove()使用和减少总距离add()：T declineKey = O(log n) + O(log n) = O(log n)

如果我们将这些值放入通式O(n · (T em +T i ) + m · T dk )中，我们得到：

O（n·log n + m·log n）

再次考虑特殊情况，即边数是顶点数的倍数，m和n可以设置为相等，我们得到：

O(n·log n) – 对于m ∈ O(n)

在我们通过实践验证这一点之前，首先要对做一些说明TreeSet。

5.3.1 TreeSet 的缺点

在添加和删除元素时，它TreeSet比慢一点，因为它在内部使用了。使用红黑树
，对节点对象和引用进行操作，而中使用的堆则映射到数组。PriorityQueueTreeMapTreeMapPriorityQueue

然而，如果图足够大，这就不再重要，正如我们将在下面的测量中看到的那样。

5.3.2 TreeSet 违反了接口定义！

在使用时我们需要考虑一件事：它违反了和接口的方法TreeSet的接口定义！remove()CollectionSet

TreeSet不会使用equals()方法来检查两个对象是否相等（这在 Java 中很常见，并在接口方法中指定）。相反，它在使用比较器时使用Comparable.compareTo()– 或。如果或返回 0，Comparator.compare()则认为两个对象相等。compareTo()compare()

删除元素时这与两个方面相关：

如果有几个节点的总距离相同，则尝试删除这样的节点可能会“意外地”删除另一个具有相同总距离的节点。
在改变总距离之前删除节点也很重要。否则该remove()方法将无法再找到它。

5.3.3 实现：NodeWrapperForTreeSet

因此，要使用TreeSet，我们必须扩展compareTo()方法来比较节点的总距离是否相同。

由于节点（以及类型参数N）也必须实现Comparable接口，我们创建一个新类NodeWrapperForTreeSet（GitHub 存储库中的类）：

class NodeWrapperForTreeSet<N extends Comparable<N>>
    implements Comparable<NodeWrapperForTreeSet<N>> {
  // fields, constructors, getters, setters

  @Override
  public int compareTo(NodeWrapperForTreeSet<N> o) {
    int compare = Integer.compare(this.totalDistance, o.totalDistance);
    if (compare == 0) {
      compare = node.compareTo(o.node);
    }
    return compare;
  }

  // equals(), hashCode()
}

此外，我们必须确保仅使用compareTo()在equals()将对象评估为相等时返回0的类作为节点类型。在我们的示例中，我们使用String，它满足了这一要求。

5.3.4 GitHub 上的完整代码

您可以在 GitHub 存储库中的 DijkstraWithTreeSet 类TreeSet中找到该算法。它与只有几点不同：DijkstraWithPriorityQueue

节点类型N扩展了Comparable<N>。
不是创建 a PriorityQueue，而是TreeSet创建 a 。
第一个元素被删除，pollFirst()而不是poll()。
它使用NodeWrapperForTreeSet而不是NodeWrapper。

我们是否应该避免代码重复并将通用功能放在一个类中？是的，如果在实践中要使用这两种变体。但在这里，我们仅比较这两种方法。

5.4 使用 TreeSet 运行时

为了测量运行时间，我们只需要在TestDijkstraRuntime的第 71行将类替换DijkstraWithPriorityQueue为DijkstraWithTreeSet。

下图显示了与之前的实现相比的测试结果：

使用 TreeSet 的 Dijkstra 算法的时间复杂度

预期的准线性增长清晰可见；时间复杂度如预测的那样为O(n · log n)。

5.5 带有斐波那契堆（Fibonacci heap）的 Dijkstra 算法

更合适的数据结构（尽管 JDK 中没有提供）是斐波那契堆(Fibonacci heap)
。其操作具有以下运行时：

提取最小条目：T extractMinimum = O(log n)
插入条目：T insert = O(1)
减少总距离：T declineKey = O(1)

带入通式O(n · (T em +T i ) + m · T dk )，可得：

O（n·logn+m）

对于边数是节点数的倍数的特殊情况，我们得到准线性时间，如下所示TreeSet：

O(n·log n ) – 对于 m ∈ O(n)

5.6 运行时使用斐波那契堆（Fibonacci heap）

由于 JDK 中没有合适的数据结构，我使用了Keith Schwarz 的斐波那契堆（Fibonacci heap）实现
。由于我不确定是否允许复制代码，所以我没有将相应的测试上传到我的 GitHub 存储库。您可以在此处看到与前两个测试相比的结果：

使用斐波那契堆的 Dijkstra 算法的时间复杂度

因此，Dijkstra 算法使用时FibonacciHeap比使用时要快一些TreeSet。

5.7 时间复杂度 - 总结

在下表中，您可以看到 Dijkstra 算法的时间复杂度概览，具体取决于所使用的数据结构。Dijkstra 本人使用数组实现了该算法，为了完整性，我也将其包括在内：

数据结构	特姆	钛	鄄	一般时间复杂度		m ∈ O(n) 的时间复杂度
Array	O(n)	O(1)	O(1)	O(n² + m)	O(n²)	O(n²)
PriorityQueue	O(log n)	O(log n)	O(n)	O(n · log n* + m · n)*	O(n²)	O(n²)
TreeSet	O(log n)	O(log n)	O(log n)	O(n · log n + m · log n)	O(n · log n)	O（n·log n）
FibonacciHeap	O(log n)	O(1)	O(1)	O(n · log n + m)	O(n · log n)	O（n·log n）