优化算法入门系列文章目录(更新中):
1. 模拟退火算法
2. 遗传算法
一. 爬山算法 ( Hill Climbing )
介绍模拟退火前,先介绍爬山算法。爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如图1所示:假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。

图1
version1:
二. 模拟退火(SA,Simulated Annealing)思想
爬山法是完完全全的贪心法,每次都鼠目寸光的选择一个当前最优解,因此只能搜索到局部的最优值。模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。以图1为例,模拟退火算法在搜索到局部最优解A后,会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点,于是就跳出了局部最大值A。
模拟退火算法描述:
若J( Y(i+1) )>= J( Y(i) ) (即移动后得到更优解),则总是接受该移动
若J( Y(i+1) )< J( Y(i) ) (即移动后的解比当前解要差),则以一定的概率接受移动,而且这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定)
这里的“一定的概率”的计算参考了金属冶炼的退火过程,这也是模拟退火算法名称的由来。
根据热力学的原理,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:
P(dE) = exp( dE/(kT) )
其中k是一个常数,exp表示自然指数,且dE<0。这条公式说白了就是:温度越高,出现一次能量差为dE的降温的概率就越大;温度越低,则出现降温的概率就越小。又由于dE总是小于0(否则就不叫退火了),因此dE/kT < 0 ,所以P(dE)的函数取值范围是(0,1) 。
随着温度T的降低,P(dE)会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程,我们以概率P(dE)来接受这样的移动。
关于爬山算法与模拟退火,有一个有趣的比喻:
爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
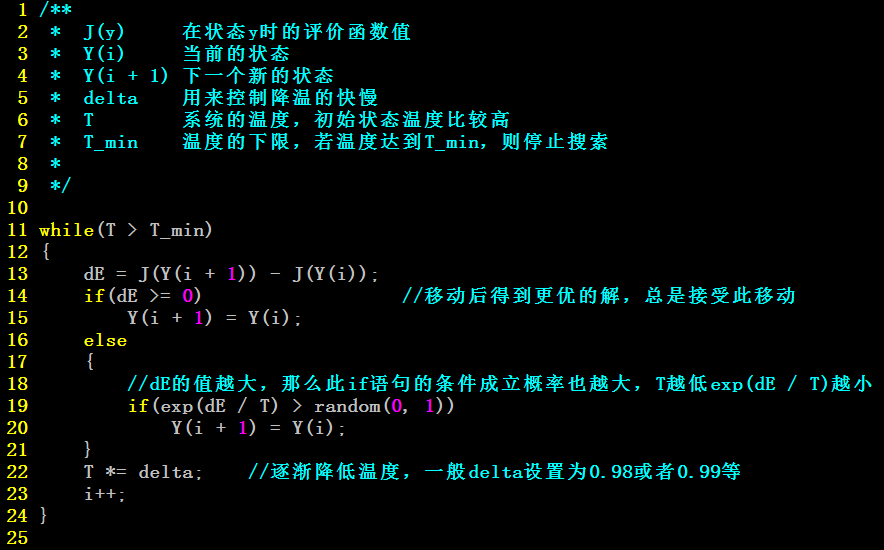
下面给出模拟退火的伪代码表示。
三. 模拟退火算法伪代码
/*
* J(y):在状态y时的评价函数值
* Y(i):表示当前状态
* Y(i+1):表示新的状态
* r: 用于控制降温的快慢
* T: 系统的温度,系统初始应该要处于一个高温的状态
* T_min :温度的下限,若温度T达到T_min,则停止搜索
*/
while( T > T_min )
{
dE = J( Y(i+1) ) - J( Y(i) ) ;
if ( dE >=0 ) //表达移动后得到更优解,则总是接受移动
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
else
{
// 函数exp( dE/T )的取值范围是(0,1) ,dE/T越大,则exp( dE/T )也
if ( exp( dE/T ) > random( 0 , 1 ) )
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
}
T = r * T ; //降温退火 ,0<r<1 。r越大,降温越慢;r越小,降温越快
/*
* 若r过大,则搜索到全局最优解的可能会较高,但搜索的过程也就较长。若r过小,则搜索的过程会很快,但最终可能会达到一个局部最优值
*/
i ++ ;
}
version2:
模拟退火算法是用来求解最优化问题的算法。比如著名的TSP问题,函数最大值最小值问题等等。接下来将以如下几个方面来详细介绍模拟退火算法。
1. 模拟退火算法认识
爬山算法也是一个用来求解最优化问题的算法,每次都向着当前上升最快的方向往上爬,但是初始化不同可能
会得到不同的局部最优值,模拟退火算法就可能跳出这种局部最优解的限制。模拟退火算法是模拟热力学系统
中的退火过程。在退火过程中是将目标函数作为能量函数。大致过程如下
初始高温 => 温度缓慢下降=> 终止在低温 (这时能量函数达到最小,目标函数最小)
在热力学中的退火过程大致是变温物体缓慢降温而达到分子之间能量最低的状态。设热力学系统S中有有限个且
离散的n个状态,状态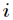
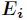
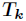
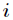
模拟退火算法也是贪心算法,但是在其过程中引入了随机因素,以一定的概率接受一个比当前解要差的解,并且
这个概率随着时间的推移而逐渐降低。
2. 模拟退火算法描述
若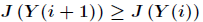
若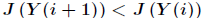
逐渐降低。这个概率表示为
由于是退火过程,所以dE < 0,这个公式说明了温度越高出现一次能量差为dE的降温概率就越大,温度越低,
出现降温的概率就越小,由于dE总是小于0,所以P(dE)取值在0到1之间。伪码如下
模拟退火样例1:
费马点问题求解
poj2420题目:http://poj.org/problem?id=2420
题意:给n个点,找出一个点,使这个点到其他所有点的距离之和最小,也就是求费马点。
由于现在还未能掌握模拟退火的具体方法,不知怎么取随机数,看了好多个版本的代码还是未能想明白,所以先贴代码先,以后再思考。
代码1:
这个方法不太具有普遍性,有些题目可能不太适用,因为它是一个点朝四个方向按一定方向搜索,然后再逐步缩小步长。代码写的简单多了,但这种做法有时候会错。。
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <math.h>
#define N 1005
#define eps 1e-8 //搜索停止条件阀值
#define INF 1e99
#define delta 0.98 //温度下降速度
#define T 100 //初始温度
using namespace std;
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0}; //上下左右四个方向
struct Point
{
double x, y;
};
Point p[N];
double dist(Point A, Point B)
{
return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
double GetSum(Point p[], int n, Point t)
{
double ans = 0;
while(n--)
ans += dist(p[n], t);
return ans;
}
//其实我觉得这玩意儿根本不叫模拟退火
double Search(Point p[], int n)
{
Point s = p[0]; //随机初始化一个点开始搜索
double t = T; //初始化温度
double ans = INF; //初始答案值
while(t > eps)
{
bool flag = 1;
while(flag)
{
flag = 0;
for(int i = 0; i < 4; i++) //上下左右四个方向
{
Point z;
z.x = s.x + dx[i] * t;
z.y = s.y + dy[i] * t;
double tp = GetSum(p, n, z);
if(ans > tp)
{
ans = tp;
s = z;
flag = 1;
}
}
}
t *= delta;
}
return ans;
}
int main()
{
int n;
while(scanf("%d", &n) != EOF)
{
for(int i = 0; i < n; i++)
scanf("%lf %lf", &p[i].x, &p[i].y);
printf("%.0lf\n", Search(p, n));
}
return 0;
}
代码2:
这个代码符合上面模拟退火的伪代码,但是下一个状态到底应该怎么取?随便?我看有些方法是乘以步长,有些乘以角度等等。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
using namespace std;
int n;
double xx,yy,ans,t;
struct point{double x,y;}p[105];
double sqr(double x){return x*x;}
double dis(double x,double y,point p)
{return sqrt(sqr(x-p.x)+sqr(y-p.y));}
double getsum(double x,double y)
{
double tmp=0;
for(int i=1;i<=n;i++)
tmp+=dis(x,y,p[i]);
return tmp;
}
int main()
{
srand(time(0));
while(scanf("%d",&n)!=EOF)
{
xx=yy=0;ans=1e20;t=100000;
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
xx+=p[i].x;yy+=p[i].y;
}
xx/=n;yy/=n;
ans=getsum(xx,yy);
double tmp,x,y;
while(t>0.02)
{
x=y=0;
for(int i=1;i<=n;i++)
{
x+=(p[i].x-xx)/dis(xx,yy,p[i]);
y+=(p[i].y-yy)/dis(xx,yy,p[i]);
}
tmp=getsum(xx+x*t,yy+y*t);
if(tmp<ans)
{ans=tmp;xx+=x*t,yy+=y*t;}
else if(log((tmp-ans)/t)<(rand()%10000)/10000.0)
{ans=tmp;xx+=x*t,yy+=y*t;}
t*=0.9;
}
printf("%.0lf\n",ans);
}
return 0;
}代码3:
下面的代码也符合伪代码的步骤,但是没有以一定概率接受新的状态那个代码,到底什么时候需要?什么时候不需要?
大致步骤如下:
1、随机选取一个合适的控制条件T作为开始
2、随机选取P个起始点,作为可行解
3、分别依据内能更新这P个可行解
4、减小控制条件T,直到终止条件
#include<iostream>
#include<cmath>
#include<ctime>
#include<cstdio>
using namespace std;
const int MAXN=100+10;
const int KMEAN=30;
const double INF=1<<30;
const double eps=1e-8;
const double PI=3.141592653;
double x=10000.0,y=10000.0;
int n;
struct Point
{
double x,y;
}myPoint[MAXN],myK[KMEAN];
double dis[KMEAN];
double GetMinDis(double tx,double ty)
{
double temp=0;
for(int i=0;i<n;i++)
{
temp+=sqrt((tx-myPoint[i].x)*(tx-myPoint[i].x)+(ty-myPoint[i].y)*(ty-myPoint[i].y));
}
return temp;
}
int main()
{
int i,j;
double temp;
while(scanf("%d",&n)!=EOF)
{
srand((unsigned)time(NULL));
for(i=0;i<n;i++)
scanf("%lf%lf",&myPoint[i].x,&myPoint[i].y);
for(i=0;i<KMEAN;i++)
{
dis[i]=INF;
myK[i].x=rand()%10001/10000.0*x;
myK[i].y=rand()%10001/10000.0*y;
}
for(i=0;i<KMEAN;i++)
dis[i]=GetMinDis(myK[i].x,myK[i].y);
double theta,delta=10000.0/sqrt(1.0*n);
while(delta>eps)
{
for(i=0;i<KMEAN;i++)
{
double nx=myK[i].x,ny=myK[i].y;
for(j=0;j<KMEAN;j++)
{
double tx,ty;
theta=double(rand()%10001)/10000.0*2*PI;
tx=nx+delta*cos(theta);//可改变方向
ty=ny+delta*sin(theta);
temp=GetMinDis(tx,ty);
if(temp<dis[i])
{
myK[i].x=tx;
myK[i].y=ty;
dis[i]=temp;
}
}
}
delta=0.98*delta;
}
temp=INF;
for(i=0;i<KMEAN;i++)
{
if(dis[i]<temp)
{
temp=dis[i];
}
}
printf("%.0lf\n",temp);
}
return 0;
}
这个版本的和代码3类似,都是随机K个可行解,不断更新可行解,最后再去可行解中的最小值。
//求n边形的费马点
//即找到一个点使得这个点到n个点的距离之和最小
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include<time.h>
const double inf = 1e10;
const double pi = acos(-1.0);
const int Rp = 4;//初始时随机选择一些点,不用太多
const int shift = 60;//但是方向一定要多
struct point {
double x,y;
void goto_rand_dir(double key)
{
double d=2*pi*(double)rand()/RAND_MAX;
x+=key*sin(d);
y+=key*cos(d);
}
void Get_Rand_Point(int a,int b)
{
x=rand()%a+1;
y=rand()%b+1;
}
}p[1010],randp[Rp];
double Dis(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double dis[Rp];
int main()
{
int i,j,x,y,k,m;
srand(time(NULL));
while(scanf("%d",&m)!=EOF)
{
for(i=0;i<m;i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
}
x=10000;y=10000;
double tmp;
for(i=0;i<Rp;i++)
{
dis[i]=inf;
randp[i].Get_Rand_Point(x,y);
tmp=0;
for(j=0;j<m;j++)
{
tmp+=Dis(randp[i],p[j]);
}
if(tmp<dis[i])
dis[i]=tmp;
}
double key=sqrt(1.0*(x*x+y*y));//初始的步长,要保证初始点从该点出发肯定能包括整个区域
while(key>=0.01)
{
for(i=0;i<Rp;i++)
{
for(j=0;j<shift;j++)
{
point cc=randp[i];
cc.goto_rand_dir(key);
if(cc.x<0||cc.y<0||cc.x>x||cc.y>y) continue;
tmp=0;
for(k=0;k<m;k++)
{
tmp+=Dis(cc,p[k]);
}
if(tmp<dis[i]) //如果从i点出发随机移动的点比原来的点更优,则接受该移动
{
dis[i]=tmp;
randp[i]=cc;
}
}
}
key=key*0.6;//可灵活调整
}
for(i=k=0;i<Rp;i++)
if(dis[i]<dis[k])
k=i;
printf("%.0lf\n",dis[k]);
}
return 0;
}模拟退火样例2:
函数最值问题求解
题目:http://acm.hdu.edu.cn/showproblem.php?pid=2899
题意:给出方程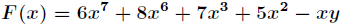

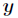
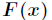
分析:本题可以用经典的二分法求解,这种方法比较简单,就不说了。主要来说模拟退火做法。之所以能够二分,是因为F(x)的导数是单调的,所以只有一个极小值,所以可以直接二分。
代码1:
模拟退火大致步骤如下,类似样例1的代码3,4:
1、随机选取一个合适的控制条件T作为开始
2、随机选取P个起始点,作为可行解
3、分别依据内能更新这P个可行解
4、减小控制条件T,直到终止条件
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <stdio.h>
#include <time.h>
#include <math.h>
#define ITERS 10
#define T 100
#define eps 1e-8
#define delta 0.98
#define INF 1e99
using namespace std;
double x[ITERS];
int Judge(double x, double y)
{
if(fabs(x - y) < eps) return 0;
return x < y ? -1 : 1;
}
double Random()
{
double x = rand() * 1.0 / RAND_MAX;
if(rand() & 1) x *= -1;
return x;
}
double F(double x, double y)
{
return 6 * x * x * x * x * x * x * x + 8 * x * x * x * x * x * x + 7 * x * x * x + 5 * x * x - y * x;
}
void Init()
{
for(int i = 0; i < ITERS; i++)
x[i] = fabs(Random()) * 100;
}
double SA(double y)
{
double ans = INF;
double t = T;
while(t > eps)
{
for(int i = 0; i < ITERS; i++)
{
double tmp = F(x[i], y);
for(int j = 0; j < ITERS; j++)
{
double _x = x[i] + Random() * t;
if(Judge(_x, 0) >= 0 && Judge(_x, 100) <= 0)
{
double f = F(_x, y);
if(tmp > f)
x[i] = _x;
}
}
}
t *= delta;
}
for(int i = 0; i < ITERS; i++)
ans = min(ans, F(x[i], y));
return ans;
}
int main()
{
int t;
scanf("%d", &t);
while(t--)
{
double y;
scanf("%lf", &y);
srand(time(NULL));
Init();
printf("%.4lf\n", SA(y));
}
return 0;
}
#include<cstring>
#include<string>
#include<iostream>
#include<queue>
#include<cstdio>
#include<algorithm>
#include<map>
#include<cstdlib>
#include<cmath>
#include<vector>
//#pragma comment(linker, "/STACK:1024000000,1024000000");
using namespace std;
#define INF 0x3f3f3f3f
double y;
double getsum(double x)
{
return 6*pow(x,7)+8*pow(x,6)+7*pow(x,3)+5*x*x-y*x;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%lf",&y);
double delte=0.98;
double t=100;
double x=0;
double ans=getsum(x);
while(t>1e-8)
{
int flag=1;
while(flag)
{
flag=0;
double temp=x+t;
if(temp>=0&&temp<=100&&getsum(temp)<ans&&fabs(ans-getsum(temp))>=1e-8)
{
x=temp;
ans=getsum(temp);
flag=1;
}
temp=x-t;
if(temp>=0&&temp<=100&&getsum(temp)<ans&&fabs(ans-getsum(temp))>=1e-8)
{
x=temp;
ans=getsum(temp);
flag=1;
}
}
t*=delte;
}
printf("%.4f\n",ans);
}
return 0;
}
还有其他样例,但是都没搞懂怎么写模拟退火的过程,感觉没有一个比较明确的方法,所以待明白之后再继续深究,我只是写了一个样例1的一个程序,过了,我也不知为什么可以过的,和样例1代码差不多,只是
z.x = s.x + dx[i] * t;
z.y = s.y + dy[i] * t;
z.x = s.x + dx[i] ;
z.y = s.y + dy[i] ;
参考链接:(加*比较重要的链接或者没看完的链接)
*大白话解析模拟退火算法











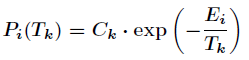
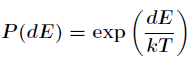
















 208
208

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








