 求解的matlab程序如下
求解的matlab程序如下
clc,clear
a=zeros(6);%邻接矩阵初始化
a(1,[2:6])=[56 35 21 51 60];
a(2,[3:6])=[21 57 78 70];
a(3,[4:6])=[36 68 68];
a(4,[5:6])=[51 61];
a(5,6)=13;
%以上是输入邻接矩阵的上三角元素
a=a';
a=sparse(a);%变换成上三角矩阵,并转化成工具箱所要的稀疏矩阵
[ST,pred]=graphminspantree(a,'method','Kruskal')%调用工具箱求最小生成树,用的是Kruskal算法
nodestr={'L','M','N','Pa','Pe','T'};%输入顶点名称的字符细胞数组,就是六个城市的代称
h=view(biograph(ST,nodestr,'ShowArrows','off','ShowWeights','on'))
h.EdgeType='segmented';%边的连接为线段
h.LayoutType='equilibrium';dolayout(h)%设置图形的属性,并刷新图形的布局
运行结果:

 题目意思:
题目意思:
 解:
解:
记
v
i
(
i
=
1
,
2
,
3
,
4
)
表
示
第
i
年
年
初
的
时
刻
,
v
5
表
示
第
四
年
年
末
的
时
刻
,
构
造
赋
权
图
G
=
(
V
,
A
,
W
)
,
其
中
V
=
{
v
1
,
.
.
.
,
v
5
}
,
A
为
弧
的
集
合
,
邻
接
矩
阵
W
=
(
w
i
j
)
5
×
5
,
这
里
w
i
j
为
v
i
到
v
j
的
费
用
,
例
如
,
w
12
=
2.5
+
0.3
−
2.0
=
0.8
,
可
计
算
得
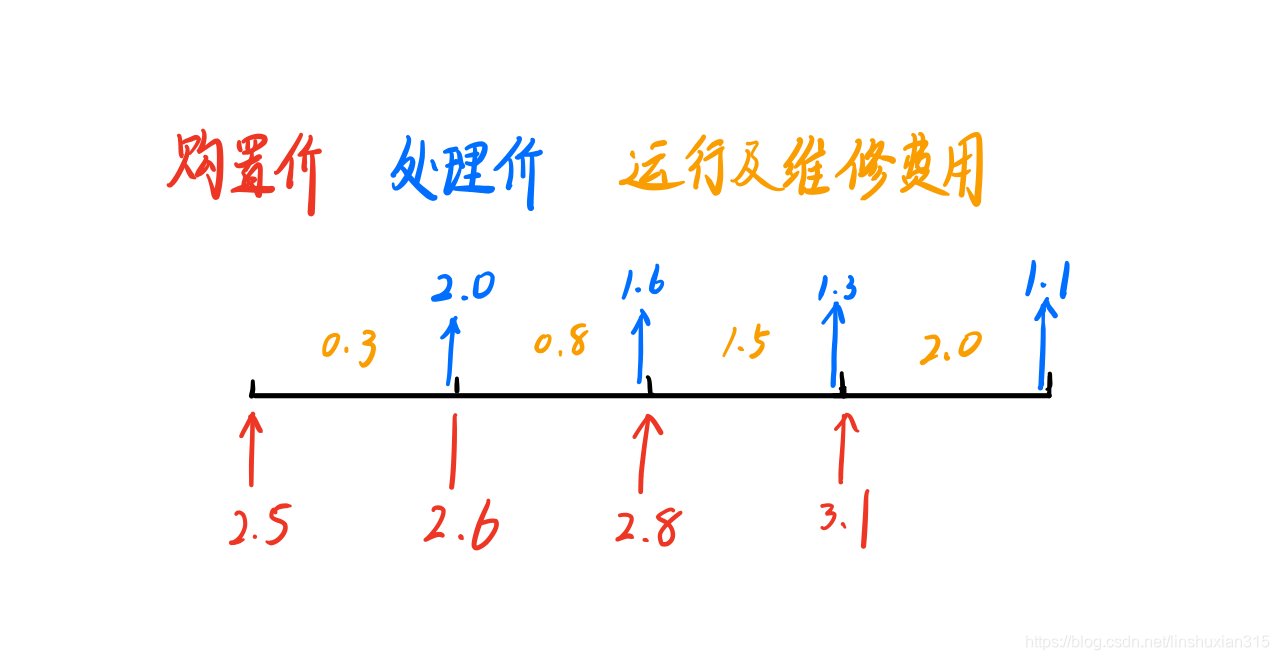
记v_i(i=1,2,3,4)表示第i年年初的时刻,v_5表示第四年年末的时刻,构造赋权图G=(V,A,W),其中V=\{v_1,...,v_5\},A为弧的集合,邻接矩阵W=(w_{ij})_{5×5},这里w_{ij}为v_{i}到v_{j}的费用,例如,w_{12}=2.5+0.3-2.0=0.8,可计算得
记vi(i=1,2,3,4)表示第i年年初的时刻,v5表示第四年年末的时刻,构造赋权图G=(V,A,W),其中V={v1,...,v5},A为弧的集合,邻接矩阵W=(wij)5×5,这里wij为vi到vj的费用,例如,w12=2.5+0.3−2.0=0.8,可计算得
 4年内用于更换、购买及运行维修总费用最省问题,归结为求图G中
v
1
v_1
v1到
v
5
v_5
v5的费用的最短路,可以使用Dijkstra标号算法求解。
4年内用于更换、购买及运行维修总费用最省问题,归结为求图G中
v
1
v_1
v1到
v
5
v_5
v5的费用的最短路,可以使用Dijkstra标号算法求解。
求解matlab的程序
clc,clear
a=zeros(5);%邻接矩阵初始化
%下面输入邻接矩阵
a(1,[2:5])=[0.8 2 3.8 6];
a(2,[3:5])=[0.9 2.1 3.9];
a(3,[4,5])=[1.1 2.3];
a(4,5)=1.4;
b=sparse(a);%有向图直接变成稀疏矩阵就可以了
[dist,path]=graphshortestpath(b,1,5,'Directed',1)%调用工具箱求最短路
结果:
表示最优更新策略为:第二年初和第三年初都换一台新机器,总费用为4万元
 解:应用最大流算法必须是单源和单汇的网络。
解:应用最大流算法必须是单源和单汇的网络。
构造一个虚拟的源点
v
s
v_s
vs,由于A,B,C的可供量分别为20,20,100,则弧
v
s
A
、
v
s
B
、
v
s
C
v_sA、v_sB、v_sC
vsA、vsB、vsC上的容量分别为20、20、100,
构造一个虚拟的汇点
v
t
v_t
vt,由于市场1、2、3、4分别记为D、F、H、I,则弧
D
v
t
、
F
v
t
、
H
v
t
、
I
v
t
Dv_t、Fv_t、Hv_t、Iv_t
Dvt、Fvt、Hvt、Ivt的容量分别为20、20、60、20.
构造赋权有向图(
V
、
E
、
W
V、E、W
V、E、W),其中
V
V
V为顶点集合,
E
E
E为弧的集合,
W
W
W为各个弧上的容量所构成的权重矩阵,具体计算时把顶点
v
s
、
A
、
B
、
C
、
D
、
F
、
H
、
I
、
v
t
v_s、A、B、C、D、F、H、I、v_t
vs、A、B、C、D、F、H、I、vt分别编号为1,2,…,9,从仓库到市场的最大流问题归结为求从
v
s
v_s
vs和
v
t
v_t
vt的最大流,可以使用Ford-Fulkerson算法求最大流。
clc,clear
a=zeros(9);
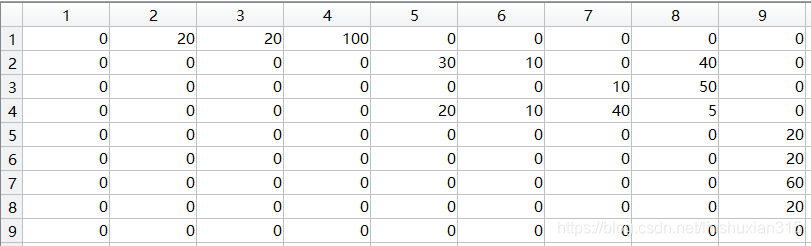
a(1,[2:4])=[20,20,100];%输入各弧上的容量
a(2,[5 6 8])=[30,10,40];
a(3,[7,8])=[10,50];
a(4,[5:8]) =[20,10,40,5];
a([5:8],9) =[20,20,60,20];
a =sparse(a)%构造工具箱需要的稀疏矩阵
[b,c]=graphmaxflow(a,1,9)%调用工具箱求最大流
程序结果:

求得从仓库运往市场的最大流量为110单位,其中市场3只能满足50单位,差10单位。

问题分析:
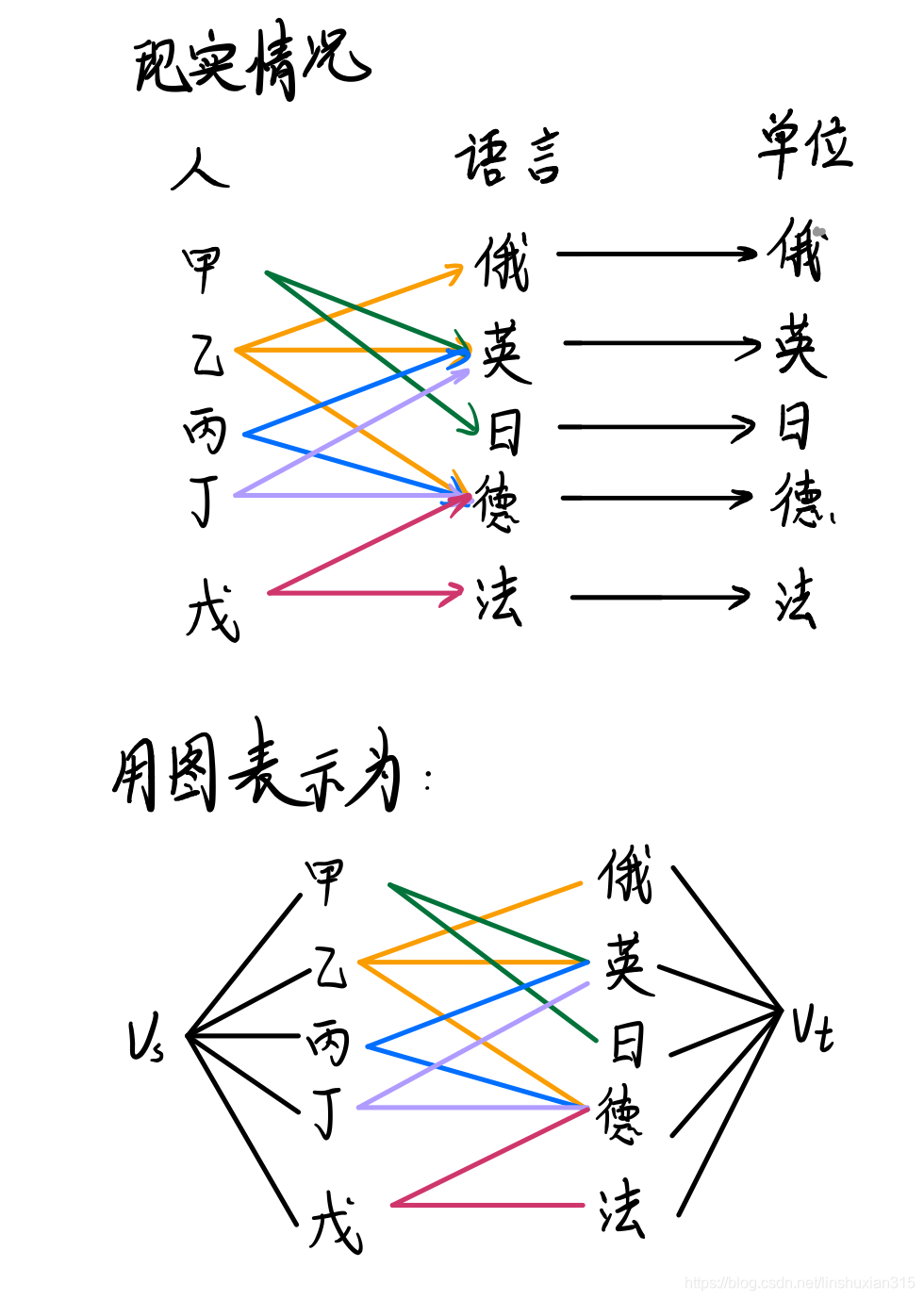
将5 个人与5 个外语语种分别用点表示,把各个人与懂得的外语语种之间用弧相连。为了求单源和单汇网络的最大流,再加一个虚拟的单源
v
s
v_s
vs,
v
s
v_s
vs与5 个人之间各有一条弧,再加一个虚拟的单汇
v
t
v_t
vt,在5 个外语语种和
v
t
v_t
vt之间各有一条弧。规定每条弧的容量为 1,求出上述网络的最大流数字即为最多能得到招聘的人数。
计算时把源点
v
s
v_s
vs,甲乙丙丁戊5 个人、俄英日德法5 个外语语种和汇点外分别编号为1,2,…,12。
clc, clear
a = zeros(12); % 容量矩阵初始化
a(1,[2:6]) =1; % 输入各弧上的容量,源点至5 个人
a(2,[8,9]) =1; % 甲懂英,日
a(3,[7,8,10]) =1; % 乙懂俄,英,德
a(4,[8,9]) =1; % 丙懂英,日
a(5,[8,9]) =1; % 丁懂英,日
a(6,[10,11]) =1; % 戊懂德,法
a([7:11],12) =1;% 5 个外语语种到汇点 ,
a =sparse(a); % 化成稀疏矩阵
[b,c] = graphmaxflow(a,1 ,12) % 调用工具箱求最大流的命令
view(biograph(c,[],'ShowWeights','on'))
求解结果:


求得只有4 个人得到招聘,乙一俄,丙一日,丁一英,戊—德,甲未能得到应聘。



建立线性规划模型,求出最大流的流量,其lingo程序如下:
model:
sets:
nodes/s,a,b,1,2,3,t/;
arcs(nodes,nodes)/s a,s b,a 1,a 2,a 3,b 1,b 2,b 3,1 t,2 t,3 t/:c,f;
endsets
data:
c=8 7 8 8 8 7 7 7 4 5 6;
enddata
n=@size(nodes);!顶点的个数;
max=flow;
@for(nodes(i)|i#ne#1 #and# i#ne#n:@sum(arcs(i,j):f(i,j))=@sum(arcs(j,i):f(j,i)));
@sum(arcs(i,j)|i#eq#1:f(i,j))=flow;
@sum(arcs(i,j)|j#eq#n:f(i,j))=flow;
@for(arcs:@bnd(0,f,c));
end
再建立一个最小费用规划模型,其lingo程序如下:
model:
sets:
nodes/s,a,b,1,2,3,t/:d;
arcs(nodes,nodes)/s a,s b,a 1,a 2,a 3,b 1,b 2,b 3,1 t,2 t,3 t/:b,c,f;
endsets
data:
b=0 0 20 24 5 30 22 20 0 0 0;
c=8 7 8 8 8 7 7 7 4 5 6;
d=15 0 0 0 0 0 -15;!最大流为15;
enddata
n=@size(nodes);!顶点的个数;
min=@sum(arcs:b*f);
@for(nodes(i):@sum(arcs(i,j):f(i,j))-@sum(arcs(j,i):f(j,i))=d(i));
@for(arcs:@bnd(0,f,c));
end
求得最小费用为240。
 解:(1)求最大流的MATLAB程序如下:
解:(1)求最大流的MATLAB程序如下:
clc, clear
a = zeros(5); % 容量矩阵初始化
a(1,[2 3]) =[10 8]; % 输入各弧上的容量
a(2,[4 5]) =[2 7];
a(3,[2,4]) =[5 10];
a(4,5) =4;
a =sparse(a); % 化成稀疏矩阵
[b,c] = graphmaxflow(a,1 ,5) % 调用工具箱求最大流的命令
view(biograph(c,[],'ShowWeights','on'))
(2)求最大流的最小费用lingo程序如下:
model:
sets:
nodes/s,1,2,3,t/:d;
arcs(nodes,nodes)/s 1,s 2,1 3,1 t,2 1,2 3,3 t/:b,c,f;
endsets
data:
b=4 1 6 1 2 3 2;
c=10 8 2 7 5 10 4;
d=11 0 0 0 -11;!最大流为15;
enddata
n=@size(nodes);!顶点的个数;
min=@sum(arcs:b*f);
@for(nodes(i):@sum(arcs(i,j):f(i,j))-@sum(arcs(j,i):f(j,i))=d(i));
@for(arcs:@bnd(0,f,c));
end
求得最小费用为55。

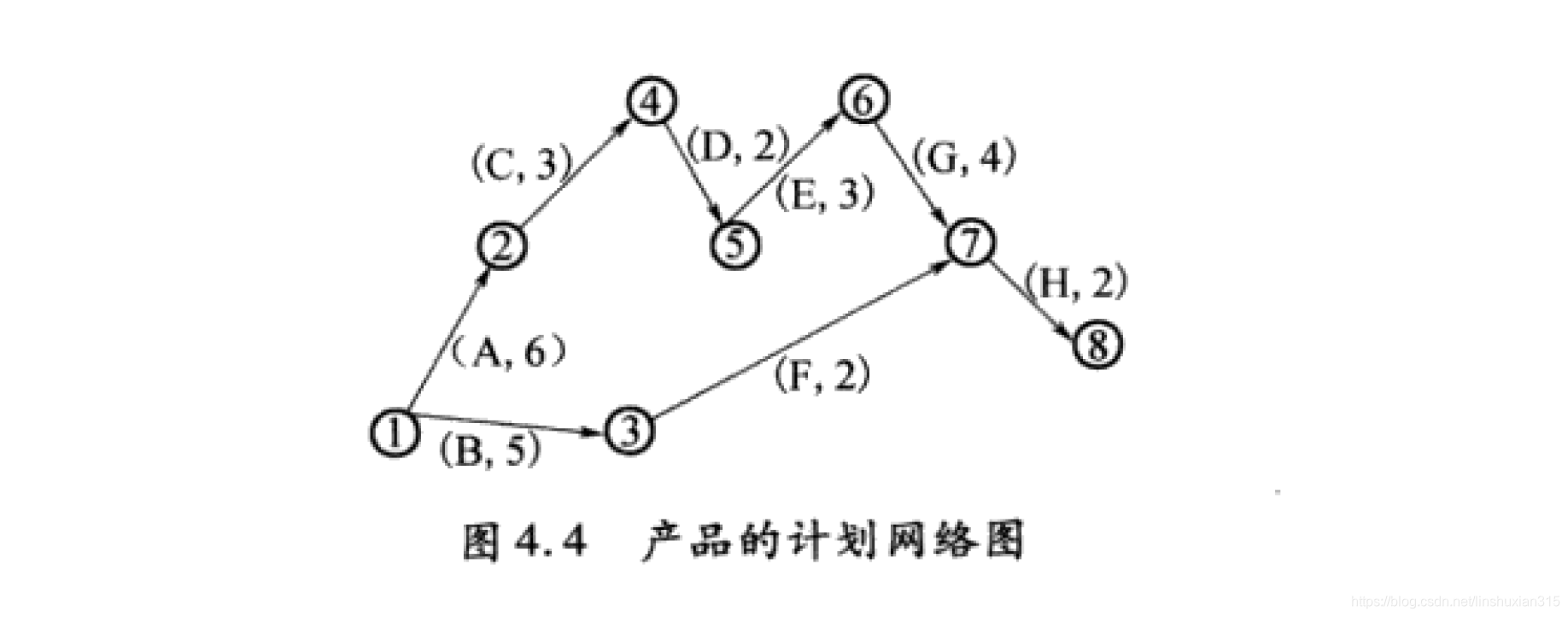
 解(1)如图所示
解(1)如图所示
 (
2
)
分
别
用
x
i
,
z
i
表
示
第
i
(
i
=
1
,
.
.
.
,
8
)
个
事
件
的
最
早
时
间
和
最
迟
时
间
,
(2)分别用x_i,z_i表示第i(i=1,...,8)个事件的最早时间和最迟时间,
(2)分别用xi,zi表示第i(i=1,...,8)个事件的最早时间和最迟时间,
(
2
)
分
别
用
x
i
,
z
i
表
示
第
i
(
i
=
1
,
.
.
.
,
8
)
个
事
件
的
最
早
时
间
和
最
迟
时
间
,
(2)分别用x_i,z_i表示第i(i=1,...,8)个事件的最早时间和最迟时间,
(2)分别用xi,zi表示第i(i=1,...,8)个事件的最早时间和最迟时间,
t
i
j
表
示
作
业
(
i
,
j
)
的
计
划
时
间
,
t_{ij}表示作业(i,j)的计划时间,
tij表示作业(i,j)的计划时间,
e
s
i
j
,
l
s
i
j
,
e
f
i
j
,
l
f
i
j
分
别
表
示
作
业
(
i
,
j
)
的
es_{ij},ls_{ij},ef_{ij},lf_{ij}分别表示作业(i,j)的
esij,lsij,efij,lfij分别表示作业(i,j)的
最
早
开
工
时
间
,
最
迟
开
工
时
间
。
最
早
完
工
时
间
,
最
晚
完
工
时
间
。
最早开工时间,最迟开工时间。最早完工时间,最晚完工时间。
最早开工时间,最迟开工时间。最早完工时间,最晚完工时间。
对
应
作
业
的
最
早
开
工
时
间
与
最
迟
开
工
时
间
相
同
,
就
得
到
项
目
的
关
键
路
径
。
对应作业的最早开工时间与最迟开工时间相同,就得到项目的关键路径。
对应作业的最早开工时间与最迟开工时间相同,就得到项目的关键路径。
为了求事件的最早开工时间与最迟开工时间xi(i=1,…,8),建立如下线性规划模型
m
i
n
∑
i
∈
V
x
i
,
min\sum_{i∈V}x_i,
mini∈V∑xi,
s . t . x j ≥ x i + t i j , ( i , j ) ∈ W , i , j ∈ V s.t.\qquad x_j≥x_i+t_{ij},(i,j)∈W,i,j∈V s.t.xj≥xi+tij,(i,j)∈W,i,j∈V
x i ≥ 0 , i ∈ V x_{i}≥0,i∈V xi≥0,i∈V
式中:V是所有的事件集合;W是所有的作业集合。
然后用下面的递推公式求其他指标。
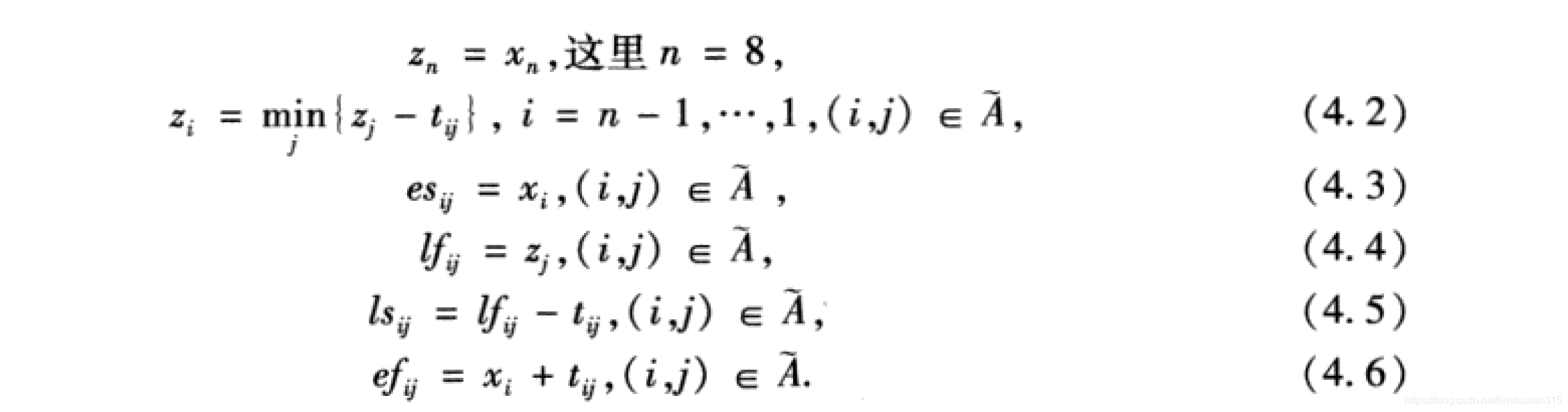



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








