正规战和游击战

一般模型

x(t)表示甲方兵力，y(t)表示乙方兵力

假设

• 每方战斗减员率取决于双方的兵力和战斗力，甲乙双方的战斗减员率分别用f(x,y)和g(x,y)表示；
• 每方非战斗减员率与本方兵力成正比；
• 甲乙双方的增援率为u(t),v(t)。

模型

f和g是不同的战争类型。

正规战争

• 甲方战斗减员率只取决于乙方的兵力和战斗力
  $$f(x,y)=-ay$$
  a表示乙方每个士兵的杀伤率
  a=r_yp_y,其中r_y表示射击率，p_y表示命中率。
  
• 忽略非战斗减员
• 假设没有增援

可以得到简单的常微分方程组：
求解该微分方程得到：

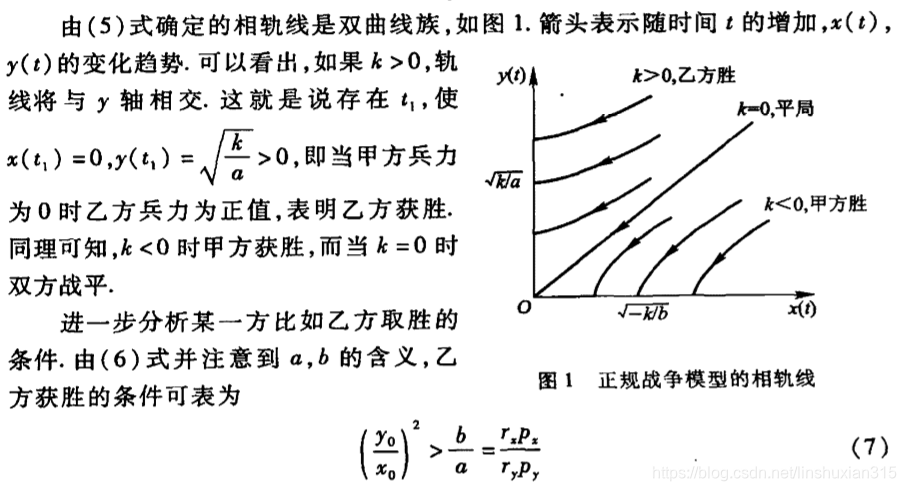因此正规战争是平方率模型

游击战争模型

在一个地区内，士兵越多，被杀伤的就越多，因此甲方战斗减员率不仅与乙方的兵力有关，而且随着甲方兵力的增加而增加。这样可以简单假设$f=cxy$;
乙方战斗有效系数$c$可表示为:
$$c=r_y{p}_y=r_y\frac{s_{ry}}{s_y}$$
其中$r_y$仍为射击率，而命中率$p_y$等于乙方一次射击的有效面积$s_{ry}$与甲方活动的面积$s_x$之比。
线性模型

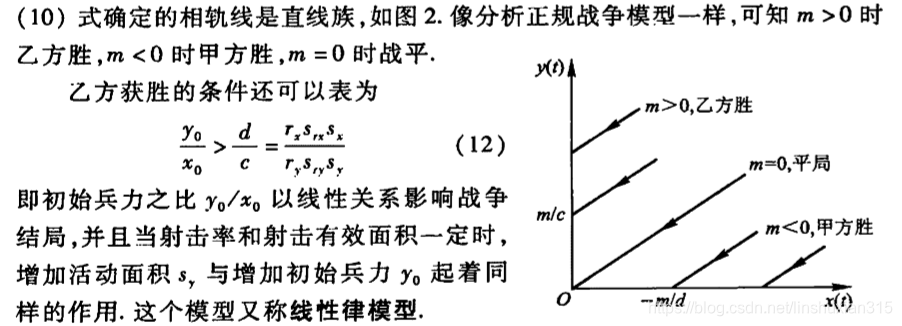
混合战争模型

甲方为游击队，乙方为正规部队。
分析

硫磺岛战役

美方和日方都是正规军，日方没有应援。

$A(t)和J(t)表示美军和日军第t天的天数，在正规战争模型(2)式中忽略非战斗减员，且v=0，再加上初始条件，有$
用求和代替积分，可得:
估计b的方法：在（22）式中，t=36，A(t)是实际统计的数据，通过统计36天的A(t)值得到${\sum }_{t=1}^{36}A(t)=2037000$,于是由$J(36)=0,J(0)=21500$可以估计出b的值：
$b=\frac{21500}{203700}=0.0106$再把这个值代入（22）式，即可算出$J(t),t=1,2,\dots ，36$