【无标题】

最新推荐文章于 2024-07-11 15:29:37 发布

linyuxi_loretta

最新推荐文章于 2024-07-11 15:29:37 发布

阅读量642

点赞数

分类专栏：线性代数文章标签：前端算法 javascript

本文链接：https://blog.csdn.net/linyuxi_loretta/article/details/126801006

版权

线性代数专栏收录该内容

7 篇文章 0 订阅

订阅专栏

Lec09. 线性相关性、基、维数dimension

the space they span 向量组所“生成”的空间

a basis for a subspace/ vector space向量空间的“基”

我们说向量组线性无关，但不会说“矩阵”线性无关

重要的背景知识：

准备求解Ax=0，

m<n, 方程个数m 较少，未知数个数n 较多

推论：在A的零空间中，除了零向量之外，还包含一些别的向量。

方程组Ax=0含有非零解non-zero（special solutions）

定义一：向量组线性无关

定义：除了系数全为零，如果存在一种组合，使得结果为零向量，那么他们是线性相关的。

平面内的任意三个向量一定是相关的，存在多余变量（自由变量）

对于矩阵A，各列是否相关？如果N(A)里存在非零向、---> 相关

假设在m维空间里，能直接判断向量组的线性相关性、零空间里只有0向量、

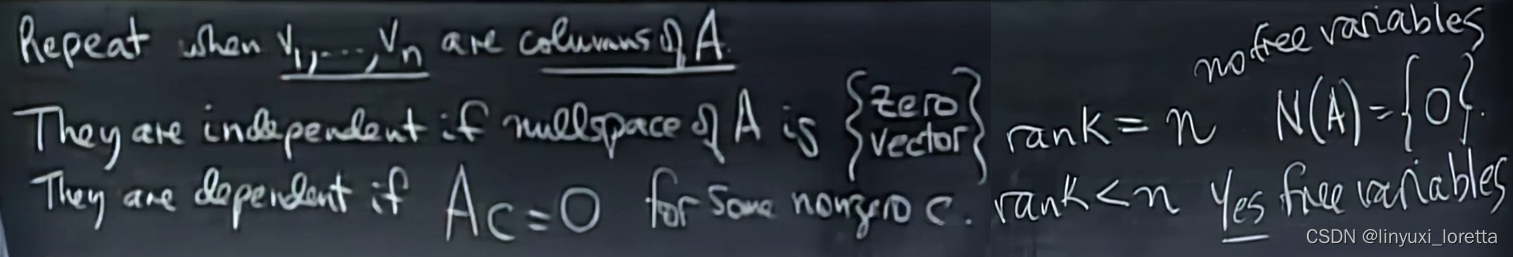
自由列free columns的实质在于：they're a combination of earlier columns

i'm often interested in the case when my vectors are popped into a matrix对矩阵里面的向量组感兴趣

so the definition of independence ---didn't talk about any matrix“线性相关性”定义并不是对矩阵来说的

the vectors didn't have to be vectors in N dimensional space没有规定向量必须在n维空间里

but most of time, the vectors we think of are columns, and we can put them in a matrix,然后将向量组的线性相关性和矩阵的零空间联系起来

定义二：向量空间的“基”

向量组“生成”一个空间

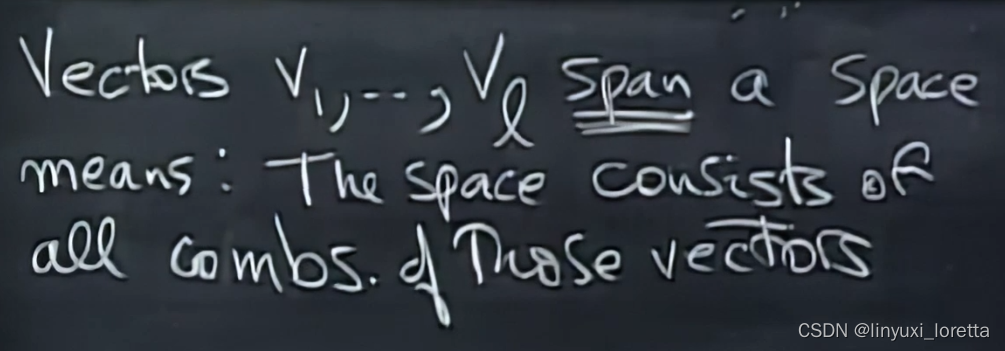
矩阵的列--->找到列所有的线性组合、等于找到矩阵的列空间、they span the column space

向量空间的一组“基”指：一个向量组、满足两个特征

子空间的基，包含子空间的全部有用信息

例子：

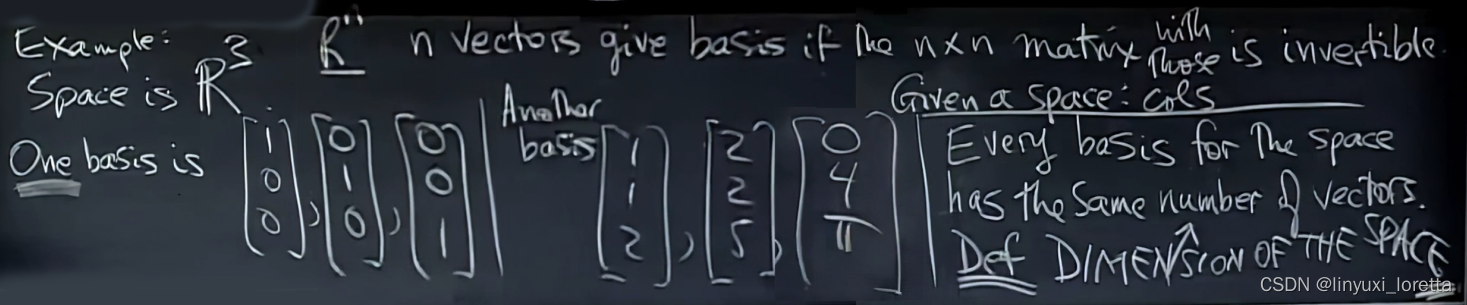
矩阵为方阵，满足什么条件、其列才能组成基？可逆

复习：

可逆：AB=BA=I，

性质：可逆矩阵一定是方阵、A的逆矩阵唯一、非奇异矩阵、满秩矩阵、rref(A)=I、

矩阵可逆、与均相关：

（1）行列式|A| 的值（≠0）、

（2）向量组相关性（无关）、

（3）方程组解的情况（齐次线性方程组Ax=0只有零解；非齐次线性方程组Ax=b总有唯一解）、

（4）矩阵A的特征值（全不为0）

虽然基有很多组，但所有基的向量个数是一样的，”维数“

总结：

线性无关：着眼于线性组合不为0

生成：着眼于所有的线性组合

基：是一组无关的向量、并生成空间

维数：表示基向量的个数

e.g.

rank(A) = # pivot columns = dimension of C(A) =2

维度为2，选2个线性无关的向量，就能生成这个空间

dim N(A)=# free variables = n-r

零空间的维数=自由向量的个数

等于0的特解、

向量空间维数是能够表示出该空间的需求的最少向量个数

矩阵的四个基本子空间

$\begin{bmatrix} 123\\ 123 \\ 258 \\ \end{bmatrix}$

矩阵不可逆，-->第三列不可能和前两列线性无关，

、因为矩阵前两个是一样的、这是个方阵，行很明显是线性相关的，

and that makes the columns dependent,

联系行空间和列空间的重要结论:

4 subspaces A is m x n

column space C(A) in R^m
null space N(A) in R^n

N(A) ，n维向量（x是n维的、）且是Ax=0的解

零空间的维度等于自由列的个数、n-r、组成零空间的向量都是n维的向量

row space = all combinations of rows = all combs of columns of A^T = C(A^T) in R^n
null space of A^T = N(A^T) = left null space of A 左零空间 in R^m

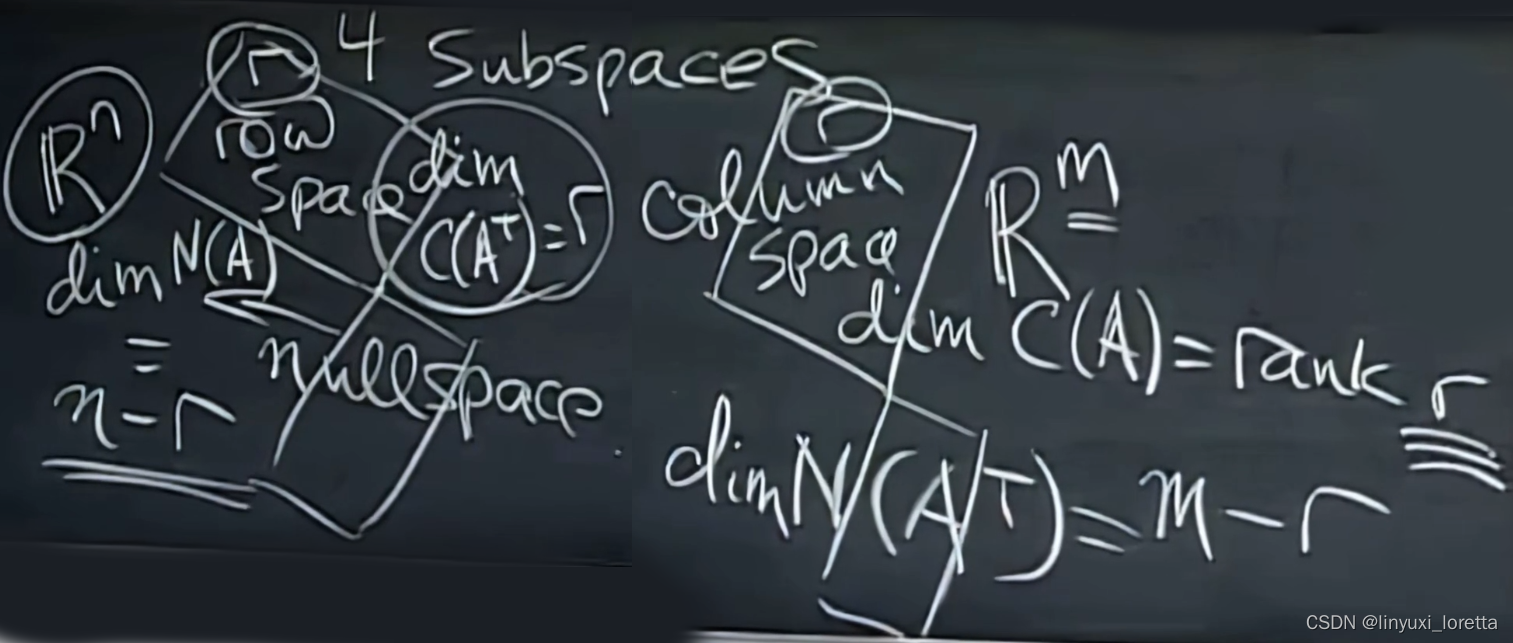
	C(A)	N(A)
basis？	pivot cols.	special solution
dimension？	r	n-r

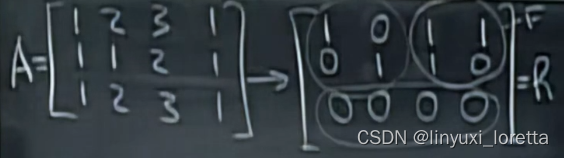
行变换不会对行空间产生影响

different col spaces C(R) ≠ C(A)

same row space； basis for row space is first r rows of R

N(A^T)：左零空间

if A^T y =0，then 向量y就在A的转置矩阵的零空间里

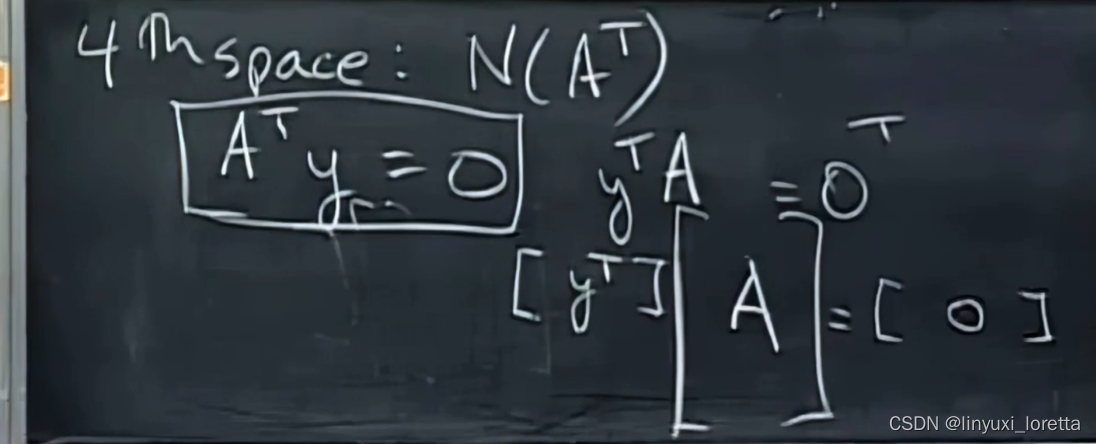
special solutions 是对Ax=0而言的，现在准备求解A转置

gauss-Jordan消元法：tack on the identity matrix （之前用于求可逆方阵的逆

E是”初等方阵“合并而成。记录变化

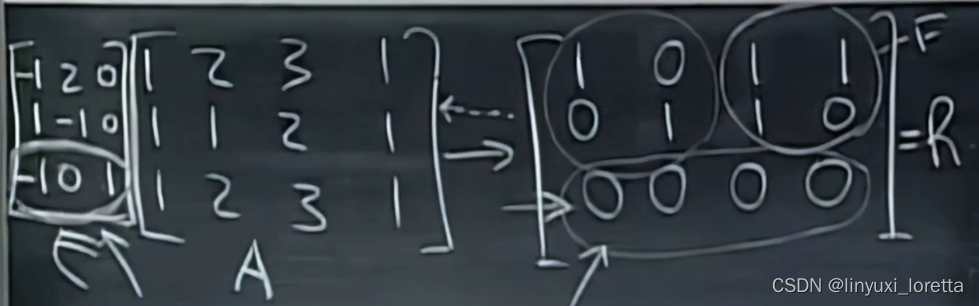
所有零行对应的E行构成基

矩阵空间

每个3x3矩阵都是一个”向量“

满足全部向量空间的八条运算律

对角矩阵的一组基：这三个矩阵线性无关、任何的对角矩阵可通过这仨组合得到，因此他们生成了对角矩阵空间

dim M = 9

symmetric dim S = 6

upper trianglar dim U=6

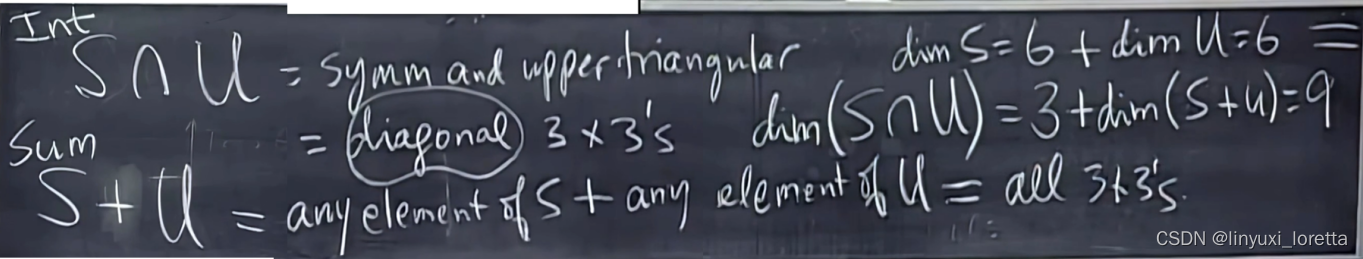
dim S +dim U = dim(S∩U) + dim(S+U)

微分方程的零空间，（解空间）

e^(ix) = cos x+ i sinx e^(-ix)= cos x- i sinx

sinx 和cosx是一组基、他们就像特殊解（special solutions）to 微分方程

线性微分方程的重要课题：寻找解空间的一组基。

解空间的维度永远是2，因为方程是二阶方程

秩1矩阵

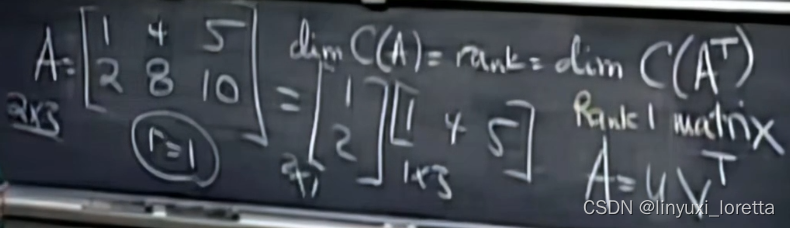
所有的秩4矩阵能构成一个子空间么？

M = all 5 x 17 matrices

subset of rank 4 matrices

问题关键：两个秩4矩阵相加、和是秩4矩阵？

r(A+B) ≤ r(A)+r(B)

要看是不是同一组积木

看两个矩阵的基元素在不在一个空间

和不封闭，not a subspace

e.g.

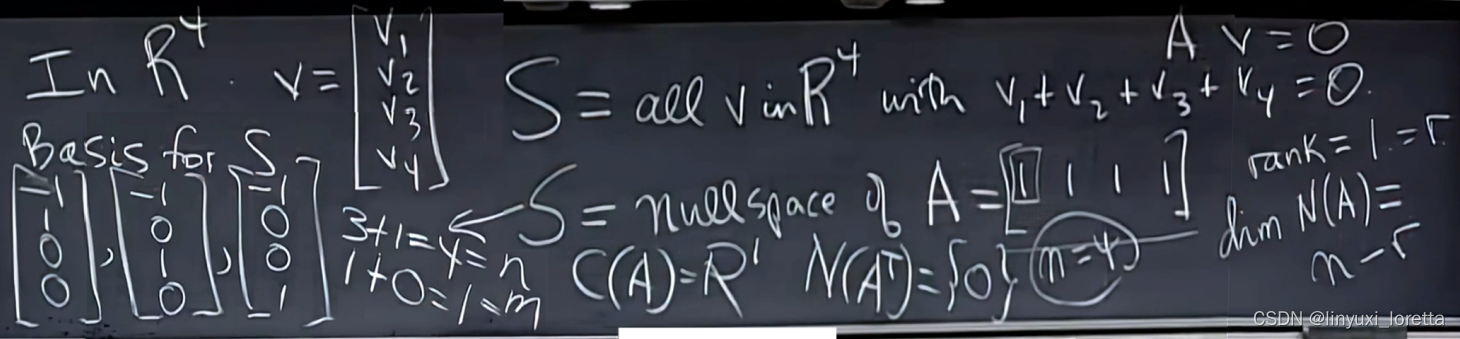
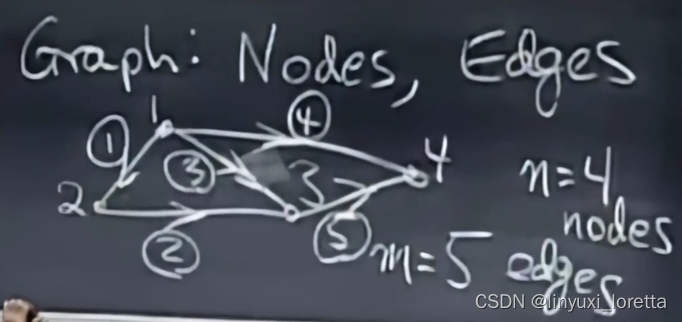
Graph 图论

图是结点和边的集合、

邻接矩阵

问题：从任意一个结点到任意其他结点、共需要走多少步

六度分离猜想

通过一些捷径、the distances come down dramatically

definite structure拓扑结构

e.g. 化学：矩阵的实际意义：有多少分子、参与了化学反应、反应的结果是什么

对矩阵进行初等行变换、可以使复杂的化学反应变得更直观

离散数学图

potential电势、电势差potential difference、currents电流

electrical network电路网络

电池内的电流是负极流向正极、因此-1和1。 -1电流流出、1电流流进，

关联矩阵incidence matrix

子图subgraph、回路loop

对于一个图来说，回路的数量和位置至关重要。”回路“意味着”相关“

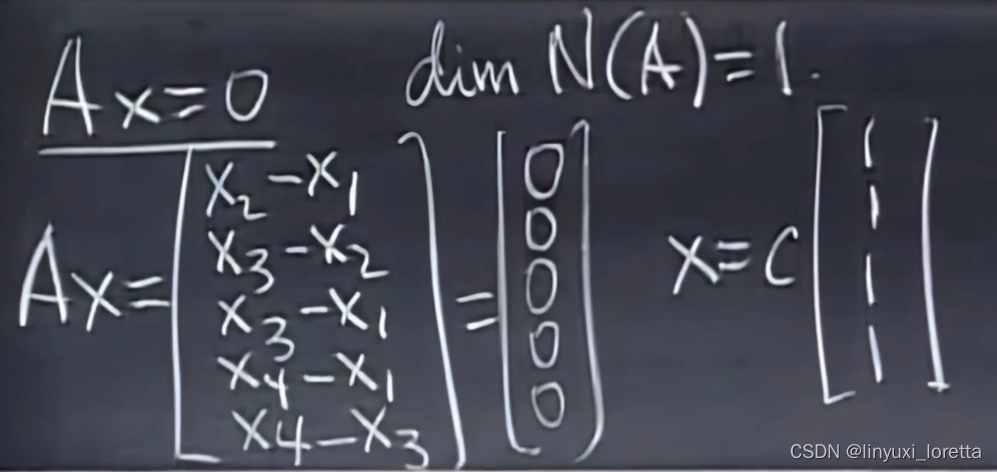
Q1：矩阵的零空间（columns 线性相关？）

矩阵A的实际意义：结点间的电势差

零空间：constant potential等电势

arbitrary任意，微积分里也存在任意常数c、以不定积分为例、通常在原函数后面加上常数c；若要确定c、必先确定初始值

对于这个例子我们先确定其中一点的电势、例如最后一个结点、典型方法是将他接地、令其电势为零，只要确定了一点电势、其他结点电势也可求出

x4=0----> r=3

A转置的零空间。 A^T y =0

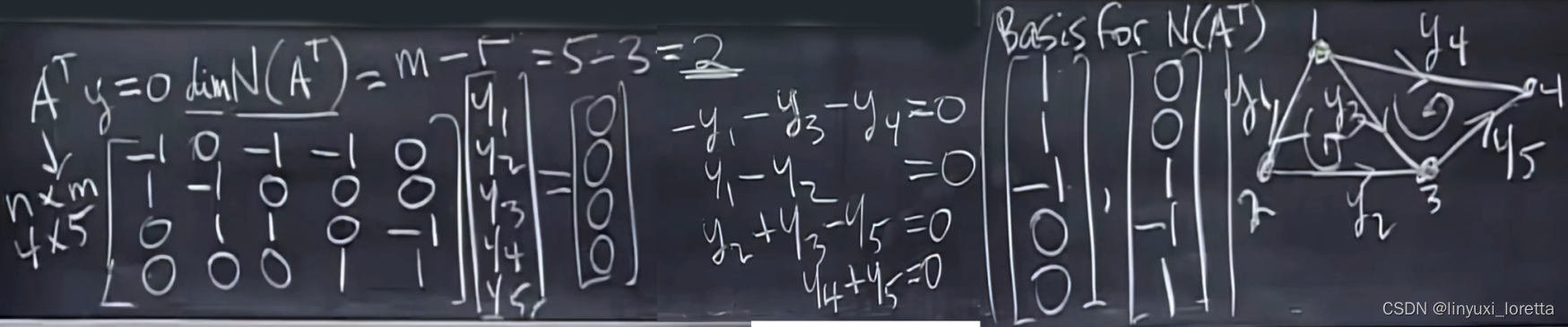
实际意义：

矩阵C 把电势差和电流current联系起来，欧姆定理：边上的电流值是电势差的倍数，这数值是边的电导conductance of the edge，电阻resistance的倒数

U=IR ，I=CU（C电导）

电势的改变产生了电流，欧姆定理告诉我们产生了多少电流

KCL是电路分析中的一个定理，对于任意一个电路中的结点、流入电流和等于流出电流和。同一结点net flow为0，节点上不会积累电荷

基尔霍夫电流定律Kirchoff's Current Law 。物理意义：电荷守恒、电荷均匀分布。回路电流法

A转置的零空间、里面的向量，--->五个满足KCL的电流值，

找一组y，电流是怎么在这个电路中流动、又不积累电荷的

分别取两个回路带个特值

维数=回路数

没有回路的图：tree

看看维度公式的意义

dim N(A^T) = m-r

#loops = # edges - (#nodes -1) (rank = n-1)

#nodes - # edges + #loops =1 Euler's formula

potential differences 电势差记作e

没考虑外部电源的影响

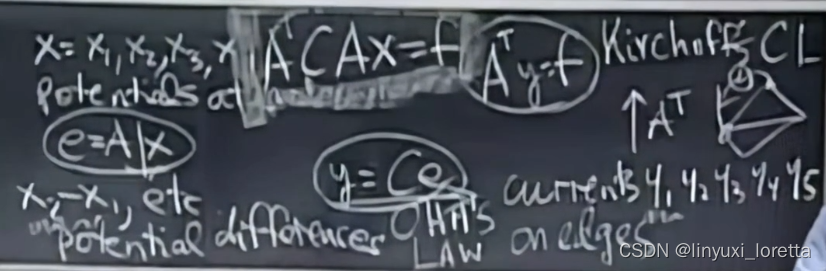
边上加电池（电压源）；在结点加电流源

A^T *A =symmetric对称

正交orthogonal

零空间和行空间都在n维空间里，交集只有零向量，正交

正交的条件？点乘 x^T y=0

用毕达哥拉斯直角三角形定理，证明：

向量长度的平方： $x^{T}x = {x_{1}}^{2}+{x_{2}}^{2}+...+{x_{n}}^{2}$

内积（inner product）是点积（dot product）的另一种说法

若两个子空间正交、他们一定不会交于某个非零向量

when 两个子空间在一个平面内正交？

注意这里的row1 row2如果要不带T写出来的话是竖着的，符合一般向量书写习惯
书写习惯，他标转置是为了表示这是行向量

e.g.

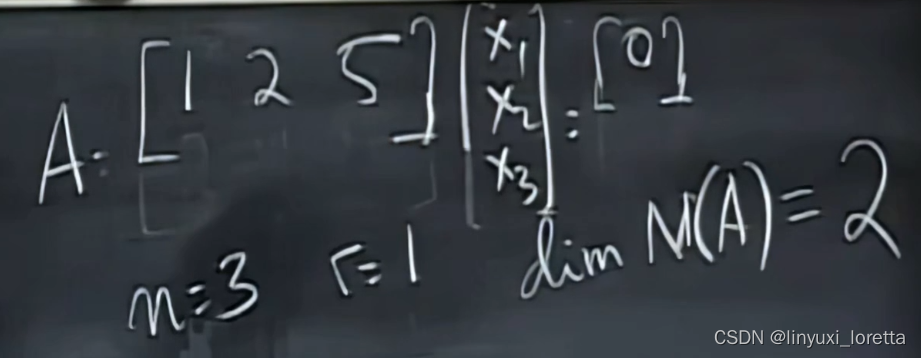
方程的零空间、是个平面

微积分，该平面的法向量（the normal vector）

orthogonal complements正交补

行空间的正交补，包含所有与之正交的向量。

即：零空间包含所有垂直于行空间的向量

线性代数：

PART1

线性代数的基本定理：关于四个基本子空间之间的关系

重点：研究维数、

PART2

已知维数

重点：研究他们的正交性

PART3

关于他们的基。 orthogonal bases正交基

如何求一个无解的方程组的解

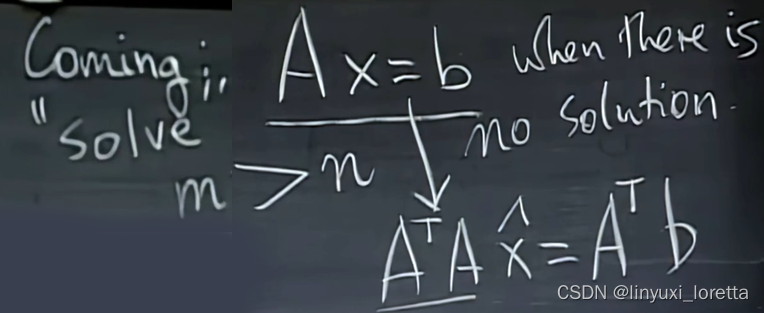
指b不在A的列空间里

方程组 m > 未知数的个数 n

e.g. 测出卫星的位置、做了一千次测量、但用来确定卫星位置的参数，也许只需要六七个就足够了

e.g. 确定体检者的脉搏频率

”坏数据“

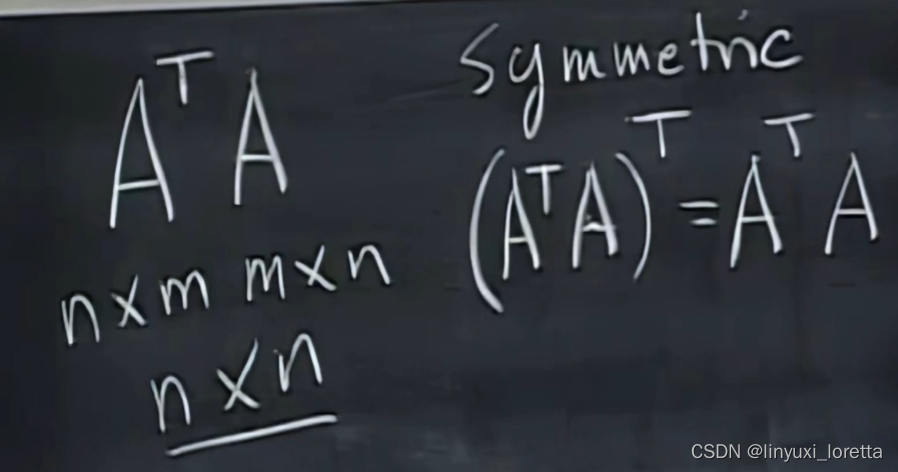
A^T *A 什么时候可逆？A满秩

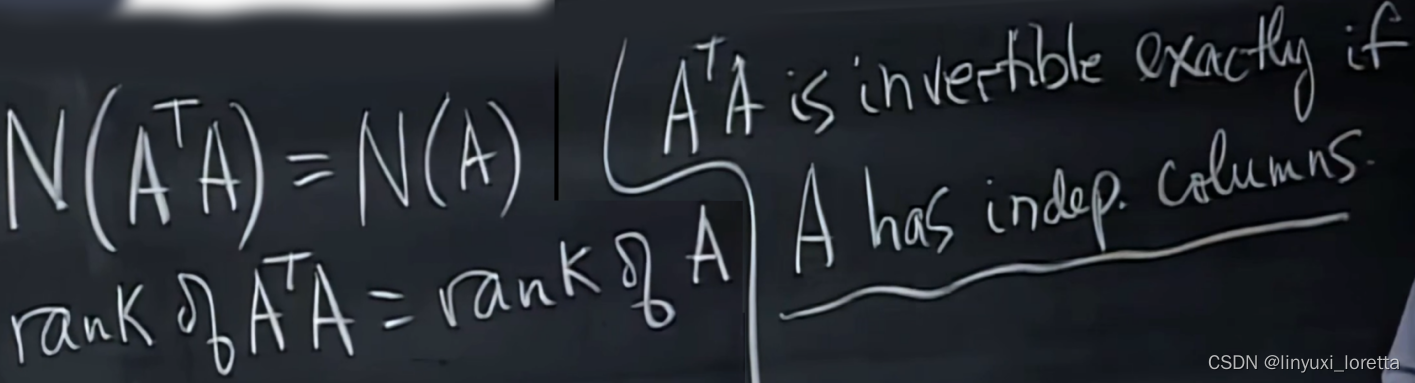
这是把b映射到a的行空间(一般是整个n空间中)，然后ata的行空间一般也是n空间，解决问题了

物理，误差分析课有专门一章讲这个A转置乘A的矩阵

rAB <=min（rA，r B）
这里是因为两矩阵相乘结果的行/列向量为原矩阵向量线性组合，必然要小于原矩阵的秩

ATA中每列是AT的各列线性组合，ATA中每行是A的各行的线性组合

这段的意义是，A列满秩可能有唯一解或无解，ATA即使变成满秩方阵也是有解的。从这个角度来看，假如b中有几个坏数据，增广矩阵消元之后会导致某几行出现方程两边无法相等，方程组也无解。ATA却必有解

投影projection

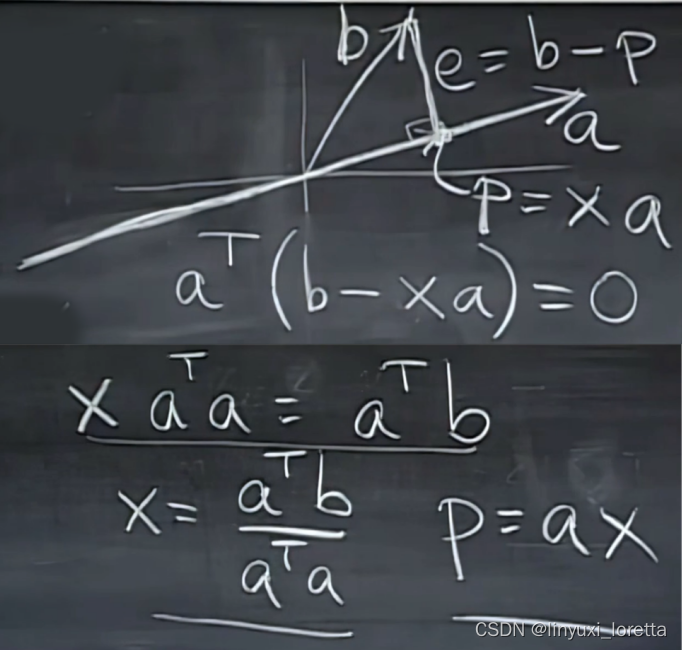
找到离线b最近的那个点，p 最优点（b在a上的投影）

e= b-p error：how mach i'm wrong by， the difference between b and p

p在a的1维子空间里、p是a的倍数

向量a点乘(b-p)，矩阵的表示方式为a的转置乘(b-p)

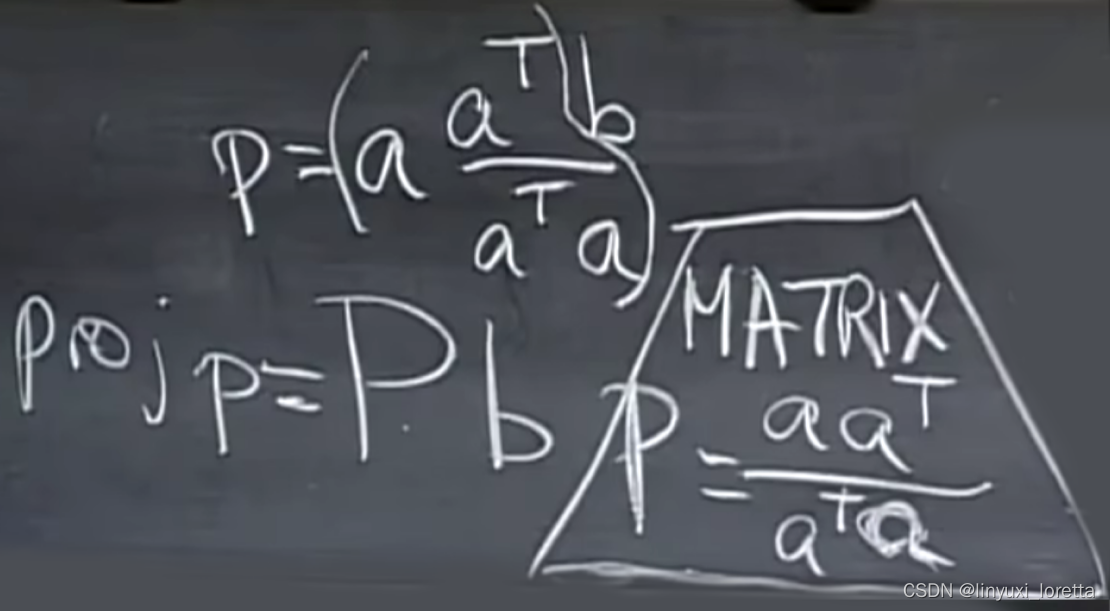
能写成分式是因为a'a是标量，但向量本身没法消

其实矩阵是不能除的，这里教授把ATA除过去是因为ATA在这里是个常数了

a^T a just a number, the length of a squared

分子是一列乘一行（一个矩阵），分母是一行乘一列（一维可看作常数）

矩阵P的性质？

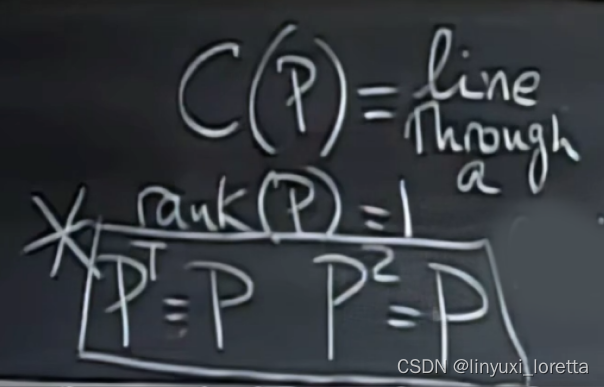
1. 列空间：A和At都是秩为1的矩阵，A At秩为1

随便用什么乘以这个矩阵、总会停在列空间里

P的列空间是由向量a生成的，所以右乘的向量b是关于a的线性组合的系数，结果p仍然是a生成的

因为只有一条直线，如果是rank=2那列空间会是一个平面

这是xy平面上所以直线是一维的如果在一个xyz平面上投影矩阵是不是就是二维的了

同解方程组套用上节最后的秩相同的结论

2.对称？yes

3.if 做两次投影会怎样？研究P平方的性质

还是P，投过一次和投过n次的结果是一样

投影矩阵的幂等性

why project？

求p---->求 $\hat{x}$

寻找合适的列组合、好让误差向量垂直于这个平面

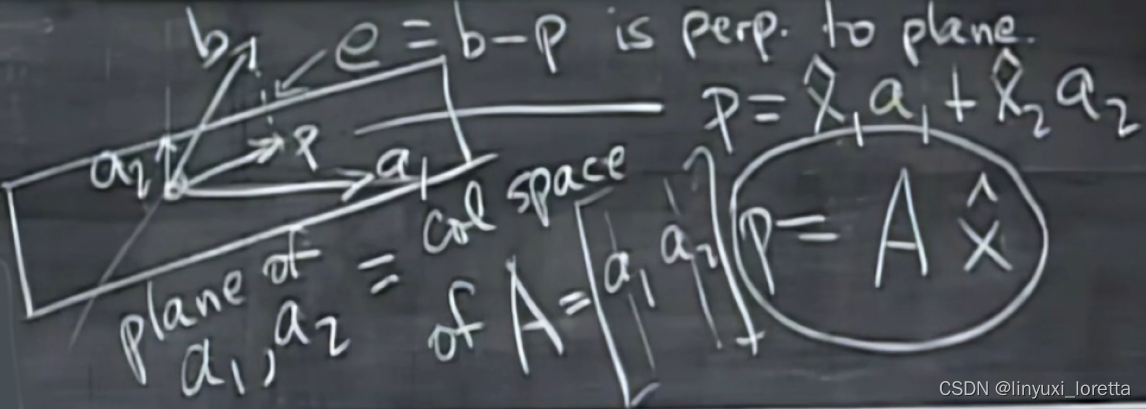
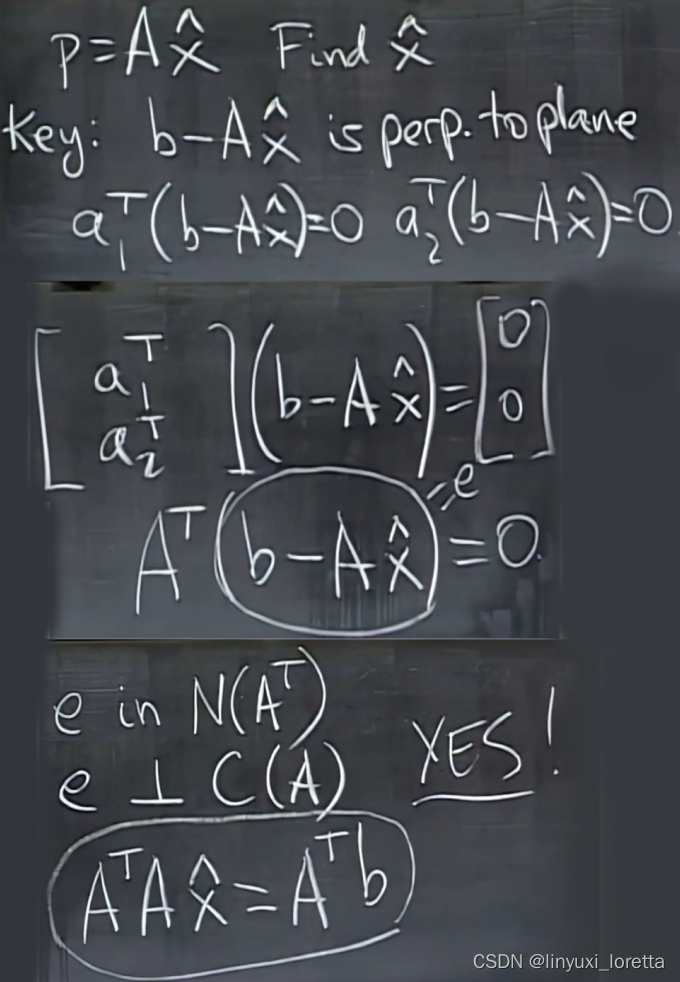
what‘s x hat？what‘s 投影？what‘s 投影矩阵？

A的列向量线性无关，r(A)=n,ATA是一个n阶方阵，而r(ATA)=r(A)=n,满秩所以ATA是可逆的

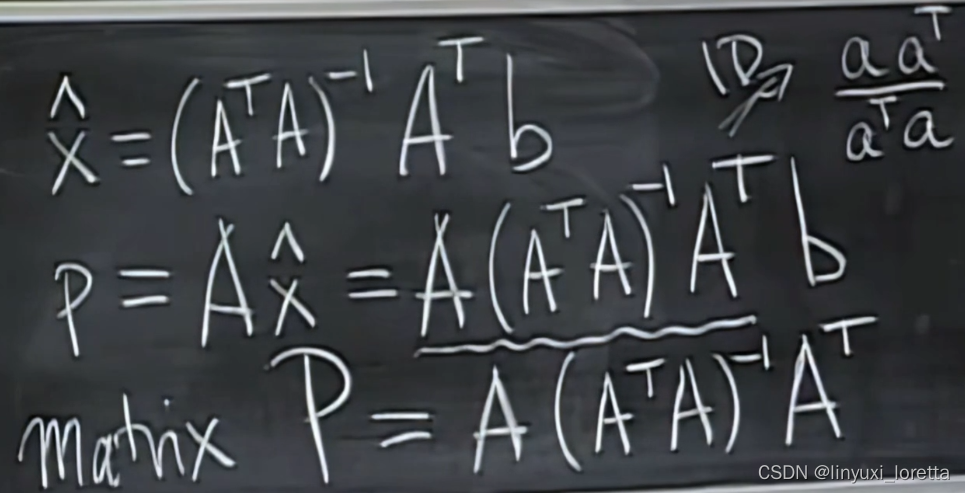
如果A可逆的话，投影矩阵为单位阵，此时p=b

因为括号的逆展开后，里面的矩阵位置要倒过来，之前的课讲到A=LU的三维矩阵的时候有讲到，只是没有写成括号逆的形式

如果A是方阵并且可逆，那列空间A一定是充满整个维度的，就不需要投影了，任何Ax=b都可以直接解

因为方阵可逆就一定是完整的n维空间，向量在空间中的投影就是本身。所以投影矩阵为I

A为可逆方阵、b本身属于三维空间、投影矩阵P=I。但如果投影到子空间、不允许这样做

P的性质？

$A^{T}A$ 和他的逆都是对称阵

一般情况下向量会有一分量在列空间里、另一分量则和他垂直

投影在做的就是，去掉后者、保留前者

if b垂直于column space、A转置的零空间里的向量

(ATA)^-1 *(ATA)=I

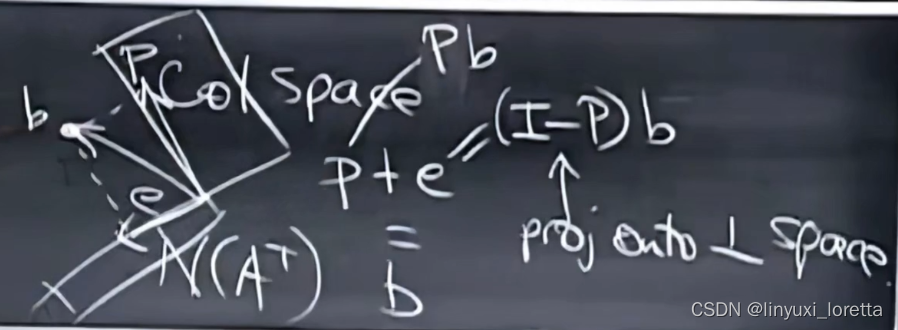
P将向量投到正交的子空间

e=b-p=b-Pb=Ib-Pb=(I-P)b

之前讲过两个相互垂直的子空间把一个完整的N维空间分成两部分，完整的N维空间就是满秩的I

应用：

有太多方程、现在我们需要求他的最优解

最小二乘法拟合一条线，使得总误差最小

总误差怎么度量？定义误差，minimize，find C和D

首先建立矩阵A、这些公式就能用了

设最优直线b=C+Dt

Ax=b无解 ---->两边乘以A转置、得到一个有解的方程 $A^{^{T}}A \hat {x}= A^{^{T}}b$ 求出最优解 x hat

best possible最接近的解，即最小化这些方程的误差平方和，least squares solution

Minimize $\left \| Ax-b \right \|^{^{2}} = \left \| e \right \|^{^{2}}$

= ${e_{1}}^{2}+{e_{2}}^{2}+{e_{3}}^{2}$

outlier 离群值，统计学中并不对其平方

所以才要做数据清洗，把点按统计特性分类，然后去除坏点

是点与点之间的距离，不是点与直线的距离

这里的误差指的是用直线预测的值（bbar或者说是y bar）和真实值（b或者说y）的差值（estimate value-ture value）

感觉就是 b是真实值 p是预测值拟合出了个线性方程预测出来的值

解p

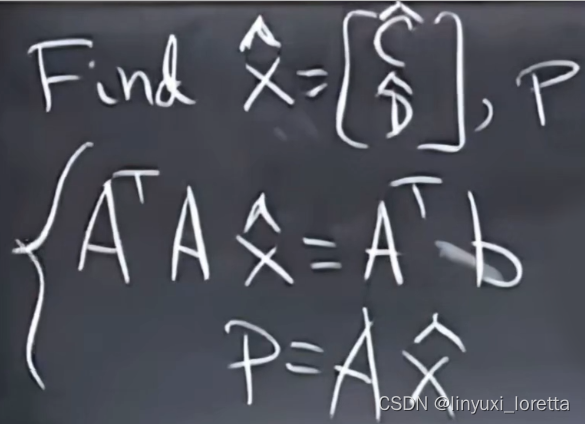
hat，来提醒：这里表示的是最优的估计，而不是完美的结果

ATA ：

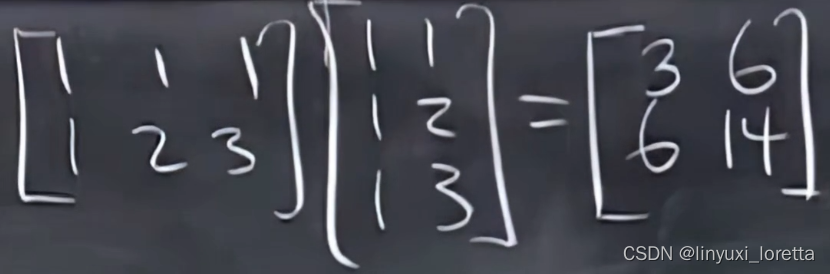
ATA ：对称、可逆、正定positive definite

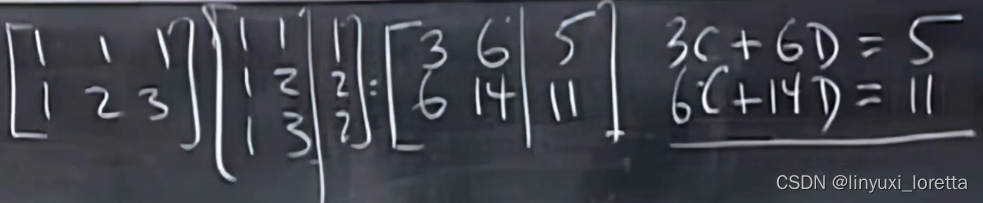
正规方程组normal equations

增广矩阵，连同右侧一起算

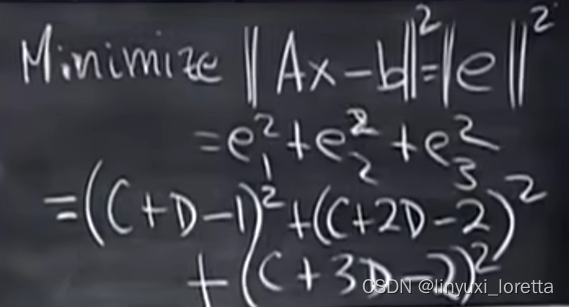
微积分法，二元函数求极值、

求偏导，令误差对C的偏导数=0，令误差对D的偏导数=0，得到两个线性方程（这就是平方的好处）

bp不应该垂直于C+Dt这条直线吗，为什么b，p横坐标相等呢

最小二乘中，误差向量e和b共享一个X坐标

向量的关系图：由C和D确定的列组合就是向量p

最优直线图：C和D定义了最优直线

A的各列线性无关，是最小二乘法成立的大前提

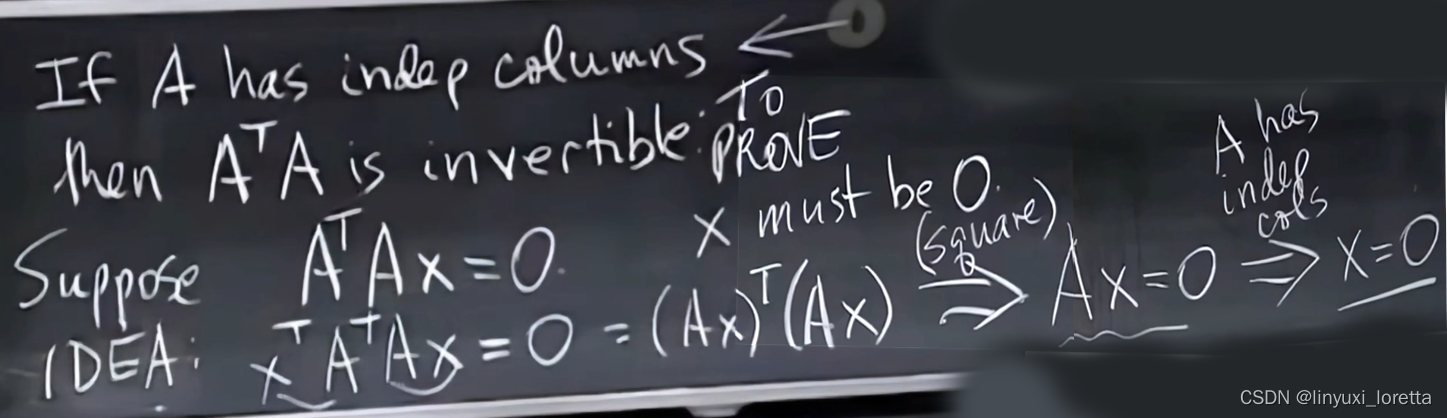
为啥yTy = 0 y一定为零向量？向量不能与自己垂直

向量长度的平方为零

搞数学时，我们要时刻记得用到命题的假设

标准正交向量组

there's one case of independent ---- when columns are sure to be independent

互相垂直的各列一定是线性无关的（排除0向量，单位向量）

Columns definitely independent if

they are perp. unit vectors （ perpendicular垂直

标准正交向量组orthonormal vectors

例：旋转矩阵

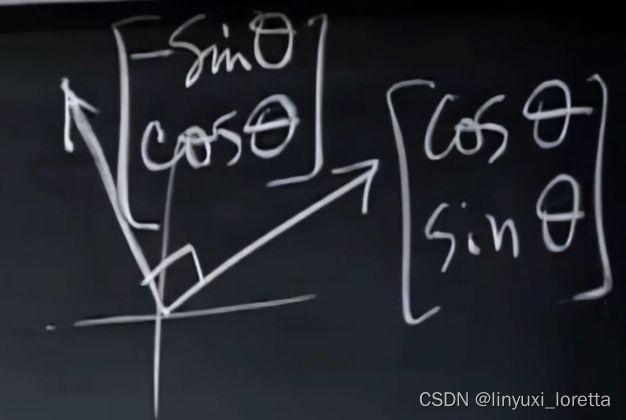
克罗内尔符号，张量分析

标准正交向量，容易操控、从不上溢或下溢

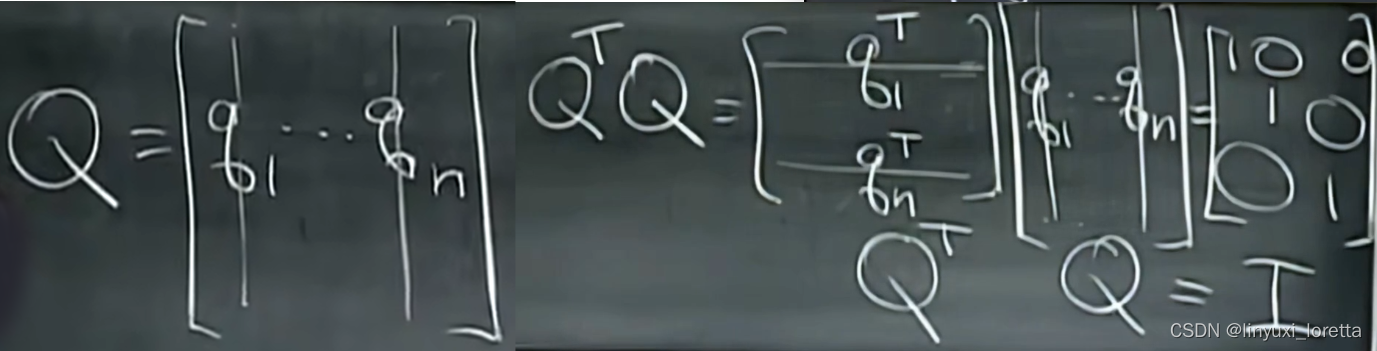
正交矩阵orthogonal matrix，方阵

orthonormal matrix标准正交

If Q is sauqre then $Q^{T}Q=I$

tells us $Q^{T} = Q^{-1}$

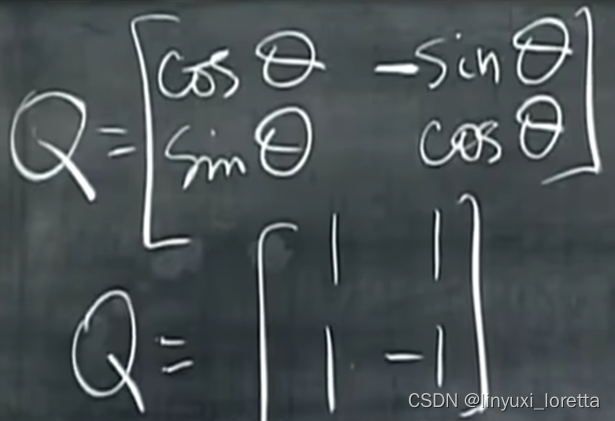
这是θ= π/4 时的情况

正交归一化，把各项变为三角函数值

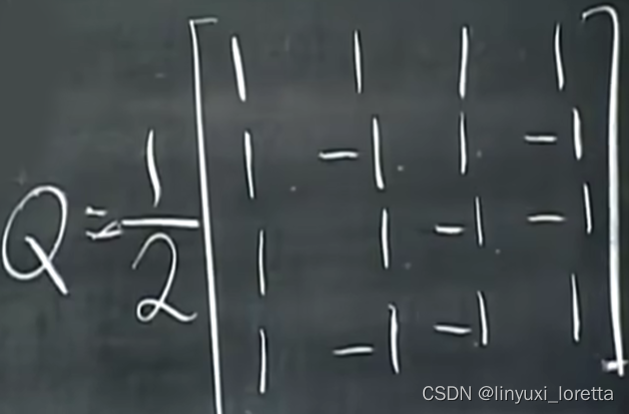
这种构造法是以阿德玛命名的 Adhemar

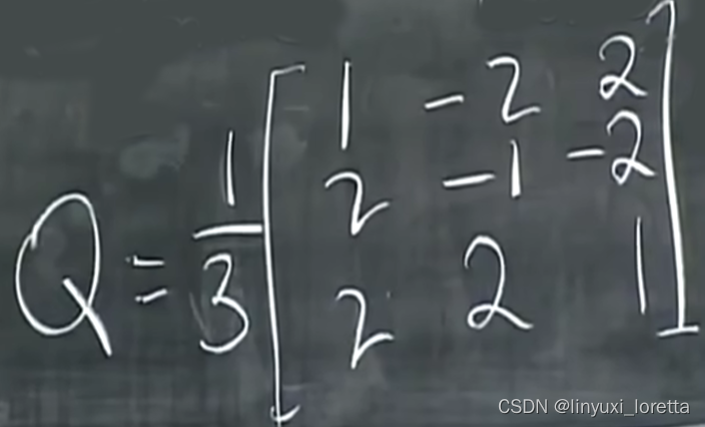
顿悟法：任意两列内积=0

格拉姆-施密特正交化法的缺点：根号常常出现

求得Q的好处：

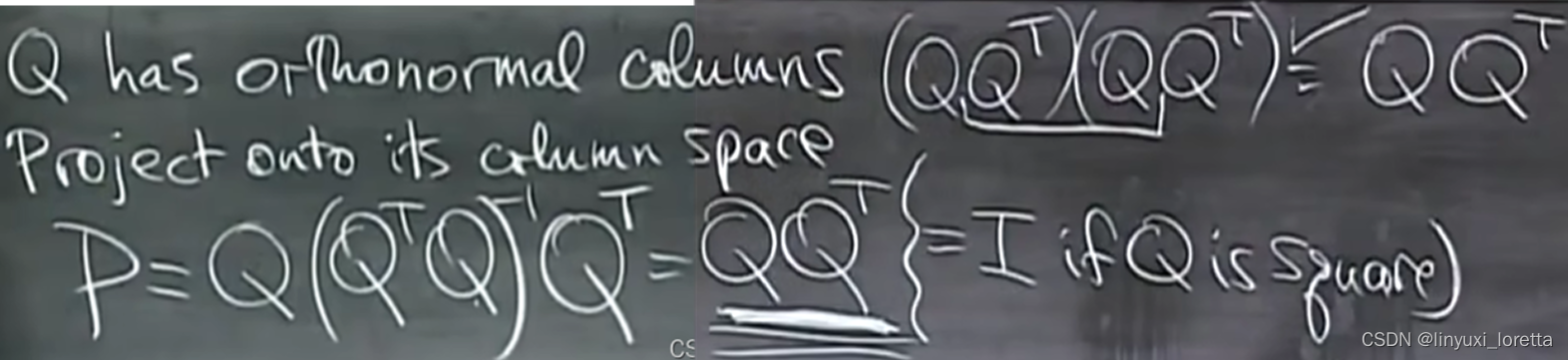
单位矩阵的逆就是单位矩阵。

如果Q各列线性无关，且是n*n方阵显然Rn空间内所有向量都在其中，投影矩阵没有意义，只是单位矩阵

投影矩阵2条性质：1. 对称 2. A^2=A

正规方程normal equation

x hat 的分量就是Q`乘b，第i个分量等于第i个基向量乘以b。如果我们有标准正交基、在第i个基方向上的投影就等于qi`b

这其实就是求余弦分量，从几何上想是给你一个单位向量作为方向，求b在这个方向上的分量

通过向标准基投影直接求倍数x。qT b=|b|cosθ

Gram-Schmidt

independent vectors a,b

---> orthogonal A,B,C

---> orthonormal $q_{1}=\frac{A}{||A||}$ $q_{2}=\frac{B}{||B||}$ $q_{3}=\frac{C}{||C||}$

$B=b- \frac{A^{T}b}{A^{T}A}A$

A ⊥B ： $A^{T}B=A^{T}\left ( b- \frac{A^{T}B}{A^{T}A}A \right ) =0$

$C=c- \frac{A^{T}c}{A^{T}A}A-\frac{B^{T}c}{B^{T}B}B$

C到A和B组合空间的投影，向量到平面的投影
减去在a上和b上的分量

e.g.

A--->Q：same column space

右乘对应着对Q矩阵的列进行线性组合，保证不会改变Q的列空间，从而使A和Q的列空间保持一致。

A=LU A=QR

$\begin{bmatrix} a_{1}&a_{2} \end{bmatrix}= \begin{bmatrix} q_{1}&q_{2} \end{bmatrix}\begin{bmatrix} q_{1}^{T}a_{1} &q_{1}^{T}a_{2} \\ q_{2}^{T}a_{1} & q_{2}^{T}a_{2} \end{bmatrix}$

格拉姆-施密特法的关键点在于，我们构造的这些q向量都是垂直于原先向量的

a1和q2是正交的所以是0

也可以从线性组合角度考虑，第一个基向量是自己，第二个是第一个和第二个的线性组合，以此类推，上三角矩阵

也可以说正交化是以前面的向量为基准，对后一个向量进行线性组合使其正交前面的所有向量，所以前面的向量没有通过后面的向量进行线性组合，所以下三角全是0

linyuxi_loretta

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【无标题】

定义：除了系数全为零，如果存在一种组合，使得结果为零向量，那么他们是线性相关的。平面内的任意三个向量一定是相关的，存在多余变量（自由变量）对于矩阵A，各列是否相关？如果N(A)里存在非零向、---> 相关假设在m维空间里，能直接判断向量组的线性相关性、零空间里只有0向量、自由列free columns的实质在于：they're a combination of earlier columns。
复制链接

扫一扫