当2k析因设计中的因子个数增加时,设计的一次完全重复所需做的试验次数迅速增大,以至超出大多数实验者所拥有的资源。例如,一个26设计的完全重复需要做64次试验,在此设计中,63个自由度中仅有6个与主效应对应,仅有15个自由度对应于二因子交互作用。其余的42个自由度与三因子交互作用及更高阶的交互作用有关。
如果实验者能合理地假定某些高阶交互作用可被忽略,则关于主效应和低阶交互作用的信息就可只做完全析因实验的一部分而求得,此类分式析因设计是在产品设计、过程设计以及过程改进方面得到最广泛应用的一类设计。
分式析因设计主要用于筛选实验,此类实验是要在众多因子中识别出有(如果有的话)大效应的那些因子,筛选实验通常在项目的早期阶段进行,那时,一开始所考虑的很多因子有可能对响应只有小的效应或没有效应。那些被识别出的重要因子在随后的实验中将被更为深入的研究分式析因设计的成功应用基于下面3个关键的思想:
(1)效应稀疏原理。当有很多变量时,系统或过程很可能被少量几个主效应和低阶交互作用所主宰.
(2)投影性质。分式析因设计可以投影到更强的(更大的)由显著性因子的子集组成的设计中去。
(3)序贯实验。可以将两个(或多个)分式析因设计序贯地组合成一个设计,用来估计所感兴趣的因子效应和交互作用。
本章将主要讨论这些原理并用几个例子来加以说明。
8.2.1定义基本原理(略)
8.2.2设计分辨度(略)
8.2.3 1/2分式设计的构造与分析
一个2k析因设计的1/2分式设计的最高分辨度构造法如下。先写出由完全2k一1析因设计的试验组成的基本设计(basic design),然后加进用它们的加号水平和诚号水平来判定取加号或减号的最高阶交互作用ABC···(K一1)作为第K个因子。因此,先写出完全的22析因设计作为基本设计,然后令因子C等于交互作用AB,就求得23-1分式析因设计。备选分式析因设计令因子C等于交互作用一AB即得。表8.2说明了这一方法。基本设计的试验次数(行数)正好,但缺少一列。用生成元I=ABC,K解出缺少的列(K),所以K=ABC···(K一1)是第K个因子,其水平由各行中各加号与减号的乘积来确定。

任一交互作用效应都可用来生成第K个因子的那一列。不过,采用任一不同于ABC···(K一1)的其他效应,都得不到最高可能分辨度的设计。
另一个构造1/2分式析因设计的方法,是把试验分解为与最高阶交互作用ABC···K相混的两个区组。每一区组是最高分辨度的2k-1分式析因设计。
1.分式析因设计在析因设计中的授影
任一分辨度为R的分式析因设计包含任一R一1个因子的子集的完全析因设计(可能有重复的)。这是一个重要的而且有用的概念,例如,实验者有几个可能感兴趣的因子,但相信只有其中的R-1个有重要的效应,于是,取分辨度为R的分式析因设计是恰当的选择。如果实验者是正确的则分辨度为R的分式析因设计将投影到R一1个显著性因子的完全析因设计上。图8.2对23-1III设计说明了这一过程,它投影到每个二因子子集的22设计上。
因为2k析因设计的1/2分式设计最大可能的分辨度是R=k,每个2k-1分式设计可投影到原来k个因子的任意(k一1)个构成的完全析因设计上。还有,2k-1分式设计又可投影到两次重复的任一k-2个因子子集构成的完全析因设计,4次重复的任一k-3个因子子集构成的完全析因设计,等等。
例8.1 考虑例6.2的渗透率实验。原来的设计是单次重复的24设计,如表6.10所示。在这个例子中,我们发现,主效应A,C,D以及交互作用AG和AD都不等于零。现在,重新回到这个实验,用24析因设计的1/2分式设计来替代原来的完全析因设计,模拟这一实验,看看将会出现什么情况。
我们用以I=ABCD为生成元的24-1分式析因设计,最高可能的分辨度为IV。要构造出这一设计,先写出基本设计(它是23析因设计),如表8.3头3列所示,基本设计有必需的试数次数(8次)。但只有3列(因子)。要求出第4个因子的水平,用I=ABCD来求出D,即D=ABC。这样,D在每次试验所取的水平就是列A,B,C的加减符号的乘积。表8.3说明了这种方法,因为生成元ABCD是正的,这一24-1IV设计就是主分式设计。图8.3是此设计的图解。

利用定义关系,每一主效应的别名是三因子交互作用。也就是说,A=A2BCD=BCD,B=AB2CD=ACD,C=ABC2D=ABD,D=ABCD2=ABC。而且,每个二因子交互作用的别名是另一个二因子交互作用。这些别名关系是AB=CD,AC=BD,BC=AD。4个主效应加上3个二因子交互作用别名对,总共占用了此没计的7个自由度。
此时,依随机顺序做这8个试验。因为已经做了完全24设计的实验,所以我们简单地从例6.2中选取8个观测到的渗透率与24-1IV设计的实验相对应。这些观测值列于表8.3最后一列,也标在图8.3中。
由此24-1IV没计求得的效应估计量见表8.4。为说明计算方法,与A效应有关的观测值的线性组合是
[A]=1/4(-45+100-45+65-75+60-80+96)=19.00→A+BCD
而对于AB效应,求得
[AB]=1/4(45-100-45+65+75-60-80+96)=-1.00→AB+CD
审核表8.4中的信息,有理由认为主效应A,C,D较大。而且,若A,C,D是重要的主效应,因为交互作用AC与AD也是显著的,则两个交互作用别名AC十BD与AD+BC自然会有大的效应。这里运用了Ockham割刀原则(William Ockham所称),即当碰到一个现象有多个不同的可能解释时,最简单的解
释通常是正确的。可以看出上述解释与例6.2中完全24设计的分析所得的结论一致。
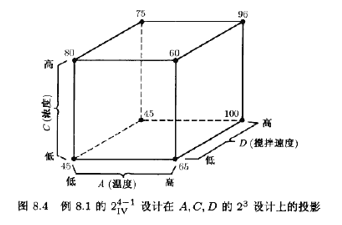
因为因子B不显著,对它可以不加考虑。因此,可以将这24-1IV设计投影到关于因子A,C,D的单次重复的23设计上,如图8.4所示。对此立方图的检查使我们对上面所得到的结论更加放心。当温度(A)处于低水平时,浓度(C有较大的正效应:而当温度处于高水平时,浓度有很小的效应。这很可能是由AC的交互作用引起的。而且,当温度处干低水平时,搅拌速度(D)可被忽略,而当温度处于高水平时,搅拌速度有较大的正效应。这很可能是由前面识别出的AD交互作用引起的。

a显著的效应是A,C,D.AC,AD
基于上述分析,可以得到用于预测实验区域内的透率的模型。此模型为
![]()
其中x1,x3,x4是表示A,C,D的规范变量(-1≤xi≤+1),像前面一样,βˆ是由效应估计得到的回归系数,因此,预测方程为
![]()
记住截距项βˆ0是实验的所有8次试验的响应值的平均值。此模型与例6.2中根据2k完全析因设计所得的模型非常相似。
#p244 例8.1

from pyDOE2 import *
import statsmodels.formula.api as smf
import pandas as pd
import statsmodels.api as sm
from sklearn import linear_model
import seaborn as sns
import matplotlib.pyplot as plt
mydoe=fracfact('a b c abc')
y =[45,100,45,65,75,60,80,96]
df =pd.DataFrame(mydoe)
df['y']=y
model = smf.ols('df.y~df[0]*df[1]*df[2]*df[3]', data=df).fit()
print(model.summary2())
Results: Ordinary least squares
====================================================================
Model: OLS Adj. R-squared: nan
Dependent Variable: df.y AIC: -448.3165
Date: 2024-04-25 11:51 BIC: -447.6809
No. Observations: 8 Log-Likelihood: 232.16
Df Model: 7 F-statistic: nan
Df Residuals: 0 Prob (F-statistic): nan
R-squared: 1.000 Scale: inf
--------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
--------------------------------------------------------------------
Intercept 35.3750 inf 0.0000 nan nan nan
df[0] 4.7500 inf 0.0000 nan nan nan
df[1] 0.3750 inf 0.0000 nan nan nan
df[0]:df[1] -0.2500 inf -0.0000 nan nan nan
df[2] 3.5000 inf 0.0000 nan nan nan
df[0]:df[2] -4.6250 inf -0.0000 nan nan nan
df[1]:df[2] 4.7500 inf 0.0000 nan nan nan
df[0]:df[1]:df[2] 4.1250 inf 0.0000 nan nan nan
df[3] 4.1250 inf 0.0000 nan nan nan
df[0]:df[3] 4.7500 inf 0.0000 nan nan nan
df[1]:df[3] -4.6250 inf -0.0000 nan nan nan
df[0]:df[1]:df[3] 3.5000 inf 0.0000 nan nan nan
df[2]:df[3] -0.2500 inf -0.0000 nan nan nan
df[0]:df[2]:df[3] 0.3750 inf 0.0000 nan nan nan
df[1]:df[2]:df[3] 4.7500 inf 0.0000 nan nan nan
df[0]:df[1]:df[2]:df[3] 35.3750 inf 0.0000 nan nan nan
--------------------------------------------------------------------
Omnibus: 1.160 Durbin-Watson: 0.390
Prob(Omnibus): 0.560 Jarque-Bera (JB): 0.712
Skew: 0.363 Prob(JB): 0.700
Kurtosis: 1.732 Condition No.: 1
====================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors
is correctly specified.
[2] The input rank is higher than the number of observations.
print(model.params)
anovatable=sm.stats.anova_lm(model)
anovatable
ValueError: shapes (16,16) and (8,) not aligned: 16 (dim 1) != 8 (dim 0)
model = smf.ols('df.y~df[0]+df[1]+df[2]+df[3]+df[0]:df[1]+df[0]:df[2]+df[0]:df[3]+df[1]:df[2]+df[1]:df[3]+df[2]:df[3]', data=df).fit()
print(model.summary2())
C:\Users\Administrator\AppData\Local\Programs\Python\Python311\Lib\site-packages\scipy\stats\_stats_py.py:1736: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=8
warnings.warn("kurtosistest only valid for n>=20 ... continuing "
C:\Users\Administrator\AppData\Local\Programs\Python\Python311\Lib\site-packages\statsmodels\regression\linear_model.py:1717: RuntimeWarning: divide by zero encountered in double_scalars
return np.dot(wresid, wresid) / self.df_resid
C:\Users\Administrator\AppData\Local\Programs\Python\Python311\Lib\site-packages\statsmodels\regression\linear_model.py:1795: RuntimeWarning: divide by zero encountered in divide
return 1 - (np.divide(self.nobs - self.k_constant, self.df_resid)
C:\Users\Administrator\AppData\Local\Programs\Python\Python311\Lib\site-packages\statsmodels\regression\linear_model.py:1795: RuntimeWarning: invalid value encountered in double_scalars
return 1 - (np.divide(self.nobs - self.k_constant, self.df_resid)
Results: Ordinary least squares
==================================================================
Model: OLS Adj. R-squared: nan
Dependent Variable: df.y AIC: -430.1565
Date: 2024-03-14 14:40 BIC: -429.5209
No. Observations: 8 Log-Likelihood: 223.08
Df Model: 7 F-statistic: nan
Df Residuals: 0 Prob (F-statistic): nan
R-squared: 1.000 Scale: inf
--------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
--------------------------------------------------------------------
Intercept 70.7500 inf 0.0000 nan nan nan
df[0] 9.5000 inf 0.0000 nan nan nan
df[1] 0.7500 inf 0.0000 nan nan nan
df[2] 7.0000 inf 0.0000 nan nan nan
df[3] 8.2500 inf 0.0000 nan nan nan
df[0]:df[1] -0.2500 inf -0.0000 nan nan nan
df[0]:df[2] -4.6250 inf -0.0000 nan nan nan
df[0]:df[3] 4.7500 inf 0.0000 nan nan nan
df[1]:df[2] 4.7500 inf 0.0000 nan nan nan
df[1]:df[3] -4.6250 inf -0.0000 nan nan nan
df[2]:df[3] -0.2500 inf -0.0000 nan nan nan
------------------------------------------------------------------
Omnibus: 0.078 Durbin-Watson: 2.881
Prob(Omnibus): 0.962 Jarque-Bera (JB): 0.288
Skew: -0.119 Prob(JB): 0.866
Kurtosis: 2.101 Condition No.: 1
==================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the
errors is correctly specified.
[2] The input rank is higher than the number of observations.
>>> print(model.params)
Intercept 70.750
df[0] 9.500
df[1] 0.750
df[2] 7.000
df[3] 8.250
df[0]:df[1] -0.250
df[0]:df[2] -4.625
df[0]:df[3] 4.750
df[1]:df[2] 4.750
df[1]:df[3] -4.625
df[2]:df[3] -0.250
dtype: float64
anovatable=sm.stats.anova_lm(model)
ValueError: shapes (11,11) and (8,) not aligned: 11 (dim 1) != 8 (dim 0)
anovatable
model = smf.ols('df.y~df[0]+df[2]+df[3]+df[0]:df[2]+df[0]:df[3]', data=df).fit()
print(model.summary2())
print(model.params)
>>> print(model.params)
Intercept 70.75
df[0] 9.50
df[2] 7.00
df[3] 8.25
df[0]:df[2] -9.25
df[0]:df[3] 9.50
dtype: float64
anovatable=sm.stats.anova_lm(model)
anovatable
>>> anovatable
df sum_sq mean_sq F PR(>F)
df[0] 1.0 722.0 722.00 222.153846 0.004471
df[2] 1.0 392.0 392.00 120.615385 0.008189
df[3] 1.0 544.5 544.50 167.538462 0.005916
df[0]:df[2] 1.0 684.5 684.50 210.615385 0.004714
df[0]:df[3] 1.0 722.0 722.00 222.153846 0.004471
Residual 2.0 6.5 3.25 NaN NaN
例8.2用来改进生产过程的25-1分式设计
在一集成电路生产线上用25-1设计来研究5个因子,以改进生产量。5个因子是:A=孔径设定(小,大),B=曝光时间(低于额定的20%,高于额定的20%),C=冲洗时间(30秒,45秒),D=掩膜尺寸(小,大),B=蚀刻时间(14.5分钟,15.5分钟)。25-1分式设计的构造如表8.5所示。构造此设计的方法是,先写出有16个试验的基本设计(A,B,C,D的一个24设计),选取ABCDE为生成元。然后设定第5个因子E=ABCD的水平。图8.5给出了这一设计的图形表示。
此设计的定义关系是I=ABCDE。因此,每一主效应的别名是一个四因子交互作用(例如,[AB]→A+BCDE),每个二因子交互作用的别名是一个三因子交互作用(例如,[AB] →AB+CDE)。这样,该设计的分辨度为V。我们希望这一25一1设计能很好地提供关于主效应和二因子交互作用的信息。
表8.6列出了这一实验的15个效应的估计量、平方和与回归系数。图8.6画出了这一实验的效应估计量的正态概率图。主效应A,B,C以及AB交互作用较大。因为别名关系,这些效应实际上是A+BCDE,



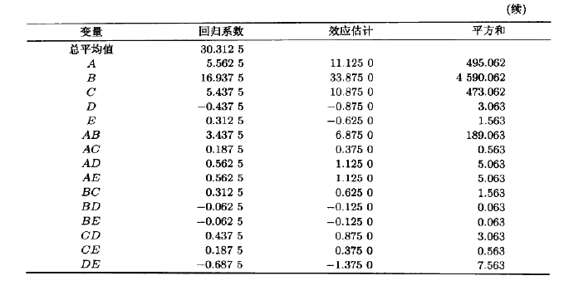

B+ACDE,C+ABDE,AB+CDE。不过,因为三因子交互作用和更高的交互作用可被忽略这一点看起来挺有道理,因此,可以认为只有A,B,C和AB是重要的效应。
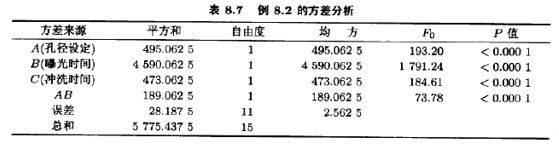
表8.7是此实验的方差分析表。模型平方和是
SS模型=SSA+SSB+SSc+SSAB=5747.25,它占了产量总变异性的99%以上。图8.7是残差的正态概率图。图8.8是残差与预测值的关系图。这两张图都是令人满意的
#p245 例8.2
from pyDOE2 import *
import statsmodels.formula.api as smf
import pandas as pd
import statsmodels.api as sm
from sklearn import linear_model
import seaborn as sns
import matplotlib.pyplot as plt
mydoe=fracfact('a b c d abcd')
y =[8,9,34,52,16,22,45,60,6,10,30,50,15,21,44,63]
df =pd.DataFrame(mydoe)
df['y']=y
model = smf.ols('df.y~df[0]+df[1]+df[2]+df[3]+df[4]+df[0]:df[1]+df[0]:df[2]+df[0]:df[3]+df[0]:df[4]+df[1]:df[2]+df[1]:df[3]+df[1]:df[4]+df[2]:df[3]+df[2]:df[4]+df[3]:df[4]', data=df).fit()
print(model.summary2())
print(model.params)
>>> print(model.params)
Intercept 30.3125
df[0] 5.5625
df[1] 16.9375
df[2] 5.4375
df[3] -0.4375
df[4] 0.3125
df[0]:df[1] 3.4375
df[0]:df[2] 0.1875
df[0]:df[3] 0.5625
df[0]:df[4] 0.5625
df[1]:df[2] 0.3125
df[1]:df[3] -0.0625
df[1]:df[4] -0.0625
df[2]:df[3] 0.4375
df[2]:df[4] 0.1875
df[3]:df[4] -0.6875
dtype: float64
anovatable=sm.stats.anova_lm(model)
anovatable
>>> anovatable
df sum_sq mean_sq F PR(>F)
df[0] 1.0 4.950625e+02 495.0625 0.0 NaN
df[1] 1.0 4.590062e+03 4590.0625 0.0 NaN
df[2] 1.0 4.730625e+02 473.0625 0.0 NaN
df[3] 1.0 3.062500e+00 3.0625 0.0 NaN
df[4] 1.0 1.562500e+00 1.5625 0.0 NaN
df[0]:df[1] 1.0 1.890625e+02 189.0625 0.0 NaN
df[0]:df[2] 1.0 5.625000e-01 0.5625 0.0 NaN
df[0]:df[3] 1.0 5.062500e+00 5.0625 0.0 NaN
df[0]:df[4] 1.0 5.062500e+00 5.0625 0.0 NaN
df[1]:df[2] 1.0 1.562500e+00 1.5625 0.0 NaN
df[1]:df[3] 1.0 6.250000e-02 0.0625 0.0 NaN
df[1]:df[4] 1.0 6.250000e-02 0.0625 0.0 NaN
df[2]:df[3] 1.0 3.062500e+00 3.0625 0.0 NaN
df[2]:df[4] 1.0 5.625000e-01 0.5625 0.0 NaN
df[3]:df[4] 1.0 7.562500e+00 7.5625 0.0 NaN
Residual 0.0 5.105508e-27 inf NaN NaN
model = smf.ols('df.y~df[0]+df[1]+df[2]+df[0]:df[1]', data=df).fit()
print(model.summary2())
print(model.params)
>>> print(model.params)
Intercept 30.3125
df[0] 5.5625
df[1] 16.9375
df[2] 5.4375
df[0]:df[1] 3.4375
dtype: float64
anovatable=sm.stats.anova_lm(model)
Anovatable
>>> anovatable
df sum_sq mean_sq F PR(>F)
df[0] 1.0 495.0625 495.0625 193.195122 2.534760e-08
df[1] 1.0 4590.0625 4590.0625 1791.243902 1.560258e-13
df[2] 1.0 473.0625 473.0625 184.609756 3.213624e-08
df[0]:df[1] 1.0 189.0625 189.0625 73.780488 3.301648e-06
Residual 11.0 28.1875 2.5625 NaN

3个因子A,B,C有较大的正效应。图8.9画出了AB或孔径设定曝光时间交互作用的图形。这图形表明,当A与B都处于高水平时产量较高。
25-1设计可压缩为由原来5个因子中的任意3个构成的23设计的两次重复(参见图8.5)。图8.10是因子A,B,C的立方体图,在8个角点上注上了平均产量。审查此立方图,显然可见,最高的产量在A,B,C都处于高水平时达到。因子D和E对平均产量有较小的效应。因此,它们的取值大小可从优化其他目标〔例如成本)考虑。


2.分式析因设计的试验顺序
用分式析因设计通常使得实验既省钱效率又高,特别是在实验可以序贯地进行时。例如,假定要研究k=4个因子(24=16个试验),则我们经常喜欢做
24-1IV分式设计(8个试验),分析其结果,然后决定下一次最好做哪些试验。当有必要去弄清模糊不清的情况时,就可再做备选的分式设计实验,完成24设计的实验。当用这种方法来完成实验设计时,两个1/2分式设计实验代表将最高阶交互作用与区组相混(此处是混杂了ABCD)的完全混区设计的两个区组。这样一来,序贯实验的结果仅仅损失了最高阶交互作用的信息。另外,在大多数情况下,从1/2分式析因设计实验中,我们会非常清楚进行下一阶段的实验时,应该加进哪些因子,去掉哪些因子,改变哪些响应变量,或者改变某些因子的取值范围等。这些可能情形以图形方式列在图8.11中。

例8.3重新考虑例8.1中的实验。用24-1IV设计初步识别出3个大的主效应:A,C,D。有两个大的效应与二因子交互作用有关:AC+BD和AD+BC。在例8.2中,根据主效应B可以忽路,初步认为重要的交互作用是AC和AD。有时,实数者具备某些工序知识,从而方便判别交互作用中那个可能更重要。不过,完成由I=-ABCD确定的备选分式设计后,总能找出显著的交互作用,以下直接列出此设计与响应:
这些效应估计量(以及它们的别名)由上述备选分式没计算得:
[A]’=24.25→A-BCD
[B]’=4.75→B-ACD
[C]’=5.75→C-ABD
[D]’=12.75→D-ABC
[AB]’=1.25→AB-CD
[AC]’=-17.75→AC-BD
[AD]’=14.25→AD-BC

这些估计量和由原来的1/2分式设计所得的估计量组合起来就得到下列效应估计量:

from pyDOE2 import *
import statsmodels.formula.api as smf
import pandas as pd
import statsmodels.api as sm
from sklearn import linear_model
import seaborn as sns
import matplotlib.pyplot as plt
mydoe=fracfact('a b c -abc')
y =[43,71,48,104,68,86,70,65]
df =pd.DataFrame(mydoe)
df['y']=y
model = smf.ols('df.y~df[0]*df[1]*df[2]*df[3]', data=df).fit()
print(model.summary2())
这些估计量与原先例6.2中作为单次重复的24析因设计的数据分析结果完全一致。显然,大的交互作用是AC和AD。
把备选分式设计添加到主分式设计可以看作是一种确认实验(confirmation experiment),这是因为它提供的信息使我们强化了关于二因子交互作用效应的最初结论。8.5节与8.6节中还将研究用于区分交互作用的组合分式析因设计的其他一些方面,确认实验并不需要这样复杂。一种非常简单的确认实验是:为了利用模型方程去预测在设计空间的某个感兴趣点(并非该设计中的点)处的响应值,那么就以该处理组合实际进行试验(也许重复几次),然后比较响应的实际值与预测值就行了,它们相当接近则表明,分式析因的解释是正确的,反之,若存在很大不同则意味若解释存在问题。由此可以看到,附加实验可用于区分混淆。
以例8.1中的24-1分式析因设计为例。实验者想要找出响应变量渗透率较高的一组条件,但是要求甲醛浓度(因子C)比较低,这表明因子A和D应该取高水平,而因子C应该取低水平。检查图8.3,可以看到,当B取低水平时,在分式析因设计中该处理组合进行了试验,得到响应观测值为100。但是B取高水平时的该处理组合不在原先设计中,故此处理组合应该是合理的确认试验。在因子A,B,D取高水平而因子C取低水平时,由例8.1的模型方程可以算得预测响应如下:

该处理组合处的响应观测值是104(参见图6.10,其中给出了完全的24析因设计的各种响应数据)。因为渗透率的观测值与预测值非常接近,所以这是一个成功的确认实验。这也表明分式析因实验的解释是正确的。
有时一个确认试验的预测值与观测值并不是这么接近,这就有必要回答两个值是否足够接近,从而有理由认为分式设计的解释是正确的,回答这个问题的一种方法是:构造该确认试验的未来响应值的预测区间(prediction interval),然后看实际观测值是否落在预测区间中,在l0.6节介绍回归模型的预测区间时,我们将用这个例子来说明这一点。

























 1826
1826

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










