数学中的特征线法是求解偏微分方程的一种方法,适用于准线性偏微分方程的求解。只要初始值不是沿着特征线给定,即可通过特征线法获得偏微分方程的精确解。 其基本思想是通过把双曲线型的准线性偏微分方程转化为两组常微分方程,再对常微分方程进行求解。两组常微分方程中的一组用于定义特征线,另一组用以描述解沿给定特征线变化。
设所需求解的准线性偏微分方程为
-
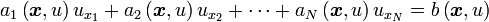 )(1)
)(1)
其中 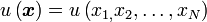 。
。
取某变量  ,令
,令  对
对  求导,可得
求导,可得
-
 (2)
(2)
若定义  ,可知
,可知
-
 (3)
(3)
即,求解的偏微分方程 (1) 的过程变作对联立的常微分方程组作积分
-
 (4)
(4)
积分过程需要给定初始条件。一般初始条件给定的形式为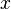 空间中的流形
空间中的流形
-
 (5)
(5)
将此曲面对应为  。
。
设想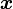 和
和  依赖于变量
依赖于变量  ,则
,则 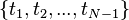 可作方程(5) 中的初始值,即
可作方程(5) 中的初始值,即
-
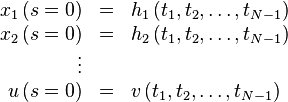 (6)
(6)
从方程组(4)和初始条件(6)确定 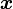 和
和  后,可以得到解的隐式形式。如果可以解析消掉
后,可以得到解的隐式形式。如果可以解析消掉 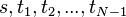 ,则可获得显式形式的解。
,则可获得显式形式的解。
一阶偏微分方程的特征线法
沿着一阶偏微分方程的特征线, 偏微分方程简化为一个常微分方程. 沿着特征线求出对应常微分方程的解就可以得到偏微分方程的解.
为了更好的解释这一方法, 考虑具以下形式的偏微分方程
-

(
假设解 u 已知, 考虑R3中的曲面 z = u(x,y). 曲面的法向量为
与曲面 z = u(x,y) 在任意点处相切. 换句话说, 解函数的图像必定是该向量场的积分曲线的并. 这些积分曲线被称作偏微分方程的特征线.







 本文介绍了一种解决偏微分方程的方法——特征线法。该方法适用于求解准线性偏微分方程,并将其转化为两组常微分方程进行求解。文中详细解释了一阶偏微分方程的特征线法,包括如何定义特征线及求解过程。
本文介绍了一种解决偏微分方程的方法——特征线法。该方法适用于求解准线性偏微分方程,并将其转化为两组常微分方程进行求解。文中详细解释了一阶偏微分方程的特征线法,包括如何定义特征线及求解过程。

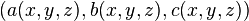
















 6689
6689

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








