基于转换的神经网络依存句法分析器

littlely_ll

已于 2024-11-08 17:07:09 修改

阅读量5.4k

点赞数 6

分类专栏：自然语言处理自然语言处理文章标签：依存分析自然语言处理神经网络

于 2018-01-06 17:41:55 首次发布

本文链接：https://blog.csdn.net/littlely_ll/article/details/78990444

版权

自然语言处理同时被 2 个专栏收录

10 篇文章

订阅专栏

自然语言处理

7 篇文章

订阅专栏

本文介绍了基于转换的神经网络依存句法分析，包括arc-eager和arc-standard两种方法。Chen和Manning提出的模型利用神经网络改进了分析器，提高了依存分析的准确性和效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

点击下方图片查看HappyChart专业绘图软件

依存句法分析是自然语言处理中一个关键的问题，一是判断给定的句子是否合乎语法，再是为合乎语法的句子给出句法结构。为了准确做出句子的依存关系，不少学者提出了一些方法，如基于图的方法，基于转换的方法等。

基于转换的依存句法分析

Yamada和Matsumoto提出了使用SVM来训练基于转换的依存分析算法。他们根据三种**分析行为（shift, right, left）**对输入的句子进行从左到右顺序构建一颗依存树，他们的算法属于自底向上（bottom-up）的分析算法。分析器算法分为两步：

使用目标节点周围上下文信息估计合适的分析行为
依据所执行的行为构建一个依存树
分析算法的核心就是提取目标结点的上下文信息，并依据模型估计最可能的分析行为（在训练模型时是由标注的依存树给出分析行为，在预测的时候是学习的模型给出）。
为了提取特征，Yamada使用一个三元组 $(p, k, v)$ 来表示一个特征， $p$ 表示距离目标节点的位置， $k$ 为特征类型， $v$ 为特征的值。对于特征类型和特征值他给出了一个表格。然后对应特征和分析行为（shift, right, left）进行训练。由于是多分类任务，Yamada使用了O vs.O的训练方法，并给出了一些评价分析器的标准：
$\frac{the number of correct parents}{the total number of parents}$
$\frac{the number of correct root nodes}{the total number of sentences}$
$\frac{the number of complete parsed sentences}{the total number of sentences}$
Nivre总结了两种基于转换的依存分析方法，一种是arc-standard parsing，另一种是arc-eager parsing。前一种是标准的自下而上的方法，如Yamada提出的方法；后一种是结合了自底而上和自上而下（top-down）的方法，这个方法是只要head和其依赖存在，就向依存图中添加弧，即使这个依赖的依赖还没有添加弧。
###arc-standard parsing
对于一个单词序列 $w_1\cdots w_n$ ，我们认为 $w_i < w_j$ ，即单词 $w_i$ 在单词 $w_j$ 的前面， $w_i\rightarrow w_j$ 表示从 $w_i$ 到 $w_j$ 有一个弧， $A$ 为 $w_i, w_j)$ 弧的集合。arc-standard parsing的构造由一个三元组 $< S, I, A >$ 构成。 $S$ 是一个栈， $I$ 是一个输入序列，是一个列表， $A$ 是依存图的弧关系。给定一个输入字符串 $W$ ，分析器的初始化为 $<nil,W,\emptyset>$ ，最后终结为 $< S, ni l, A >$ 。
那么，arc-standard分析器的策略有三种：
left-reduce转换，它通过一个左向的弧 $w_j\rightarrow w_i$ 把栈顶最上的两个元素 $w_i$ 和 $w_j$ 联系起来，并抛出 $w_i$ 。
right-reduce转换，它通过右向弧 $w_i\rightarrow w_j$ 把栈顶最上的两个元素 $w_i$ 和 $w_j$ 联系起来，并抛出 $w_j$ 。
shift转换，把 $I$ 中的下一个输入 $w_j$ 压进栈。

left-reduce和 right-reduce的约束就是一个词只能有一个依赖，即 $w_i\rightarrow w_j\bigwedge w_k\rightarrow w_j \Rightarrow w_i=w_k$ 。而shift的约束就是输入列表中不能为空。
整个过程由下图表示：
这里写图片描述

arc-eager parsing

arc-eager算法的转换过程如下：

left-arc转换，从下一个输入 $w_j$ 到栈顶的元素 $w_i$ 加一个弧 $w_j\rightarrow w_i$ 并把栈顶的元素 $w_i$ 抛出。
right-arc转换，从栈顶的元素 $w_i$ 像下一个输入 $w_j$ 添加一个弧 $w_i\rightarrow w_j$ ，并把 $w_j$ 压进栈中。
reduce转换，是抛出栈顶元素。
shift转换，是把下一个输入元素 $w_j$ 压进栈。
left-arc，right-arc和shift与arc-standard中的约束一样，而 reduce的约束是栈顶的元素已经有了一个head。具体表示如下图：

基于转换的神经网络依存分析器

由于很多的依存分析器基于很多的稀疏特征，他们的推广性较差，并且计算代价大，Chen和Manning提出了基于转换的神经网络依存分析，它使用了少量的密集特征，计算迅速，并且attachment scores有所提升。
他们使用的转换方法是arc-standard方法，前面已经叙述过。由下面的一张图展示依存分析转换的过程，其中，第三张图的每一行就是一个configuration：
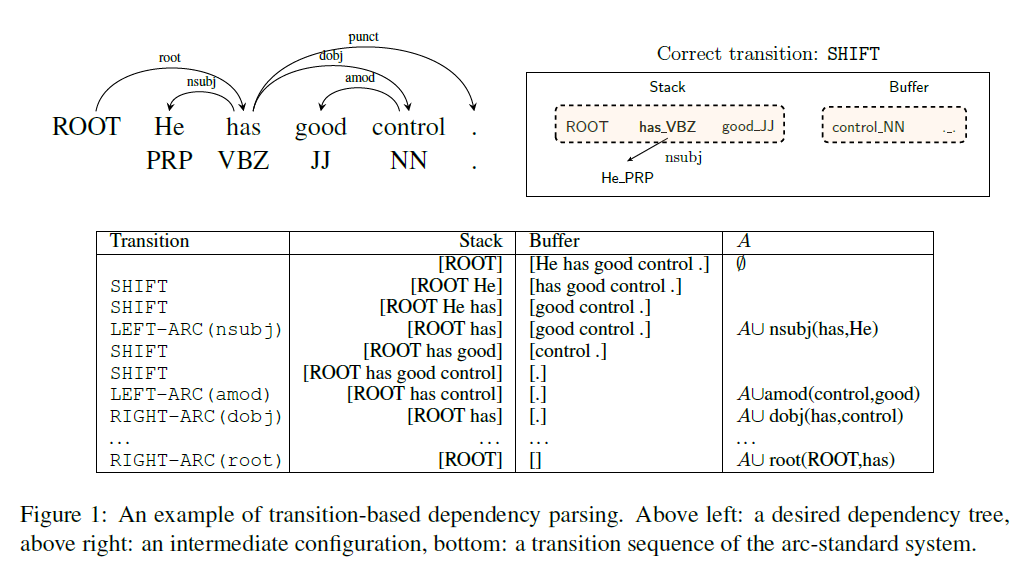
这里写图片描述

不过，这里面我有一点不懂的是，它是怎么把栈顶第二个元素抛出而不影响栈顶第一个元素的，比如在上图的第三张图中，第5行的转换为SHIFT，栈为[ROOT has good control]，经过LEFT-ARC(amod)转换后，怎么把good抛出的（计算机中，如果是栈的话，抛出栈顶第二个元素那么肯定把栈顶第一个元素已经抛出了，为什么control还在栈中呢？是不是把它又压进栈了呢，不清楚）。
这个神经网络分析器其实只有三层结构，输入层，隐含层和输出层。下图展示了分析器的层级结构：
这里写图片描述
输入层是词向量，词性标注向量和弧标签向量的拼接层；隐含层使用了一个三次方的非线性函数；输出层就是一个softmax层。其实重点在这个输入层怎么表示。
首先对于词向量，对于每一个词，使用d维的向量 $e_i^w\in R^d$ 来表示，整个词向量矩阵表示为 $E^w\in R^{d\times N_w}$ ，其中， $N_w$ 为字典大小。同样的，词性标注和弧标签也由一个d维的向量表示 $e^t_i, e^l_j \in R^d$ ，对应的词性标注和弧标签向量矩阵分别为 $E^t\in R^{d\times N_t}, E^l\in R^{d\times N_l}$ ，其中， $N_t,N_l$ 分别为词性标注和弧标签的个数。
用 $S^w, S^t, S^l$ 分别代表从单词，词性标注和弧标签抽取的集合，每一个configuration都有一个 $S^w, S^t, S^l$ 。例如，在上图的configuration中，词性标注集合 $S^t=\{lc_1(s_2).t, s_2.t, rc_1(s_2).t, s_1.t\}$ ，从左到右意思为栈顶第二个元素左子结点的词性、栈顶第二个元素的词性、栈顶第二个元素右子结点的词性、栈顶第一个元素的词性，则它们分别为PRP、VBZ、NULL、JJ，用NULL表示不存在。一般来说，最多使用目标词的子结点的子结点就够了，即 $lc_i(lc_i(s_2)).t$ ，再深的没见过。
这样我们得到了 $S^w, S^t, S^l$ ，这里面只是一个个的单词、词性及标签，并不是它们的向量表示。用 $n_w,n_t,n_l$ 分别表示选择每种类型元素的个数，则 $x^w=[e^w_{w_1};e^w_{w_2};\cdots;e^w_{w_{n_w}}]$ ，其中， $S^w=\{w_1,\cdots,w_{n_w}\}$ ，类似地可以得到 $x^t, x^l$ 。即把 $x^w, x^t, x^l]$ 代入输入层。
从输入层到隐藏层使用三次方激活函数:
$(W^w_1x^w + W^t_1x^t + W^l_1x^l +b_1)^3$
其隐层单元个数为 $d_h$ ， $W^w_1\in R^{d_h\times(d\cdot n_w)}$ ， $W^t_1\in R^{d_h\times(d\cdot n_t)}$ ， $W^l_1\in R^{d_h\times(d\cdot n_l)}$ ， $b_1\in R^{d_h}$ 为偏置。
softmax层输出多元概率 $p=softmax(W_2h)$ ，其中， $W_2\in R^{|T|\times d_h}$ ， $∣ T ∣$ 为转换类型的个数。
###参数初始化及训练
首先从训练句子和“黄金分析树”中产生训练集为 $\{(c_i,t_i)\}^m_{i=1}$ ， $c_i$ 为configuration， $t_i\in T$ 为转换。
目标函数为交叉熵损失函数加上L2正则化：
$L(\theta) = -\Sigma_ilogp_{t_i}+\frac{\lambda}{2}||\theta||^2$
其中， $\theta$ 为 $\{W^w_1, W_1^t, W_1^l, b_1, W_2, E^w,E^t,E^l\}$ 的参数集。
初始化：用预训练的词向量(使用word2vec)初始化 $E^w$ ，也可以进行随机初始化，用在(-0.01,0.01)内的数随机初始化 $E^t,E^l$
优化：使用min-batched AdaGrad，dropout(0.5)
预测：首先从configuration c中抽取对应的词向量，词性标注向量和类别标签向量，然后计算隐藏层 $h(c)\in R^d$ ，在softmax输出时，找到最大概率的转换：
$arg\quad max_{t\_is\_feasible}W_2(t, \cdot)h(c)$
然后再执行转换 $c\rightarrow t(c)$ ，直至把整个句子转换完。
Weiss等人在Chen的基础上又增加了一层隐含层和一层感知机层，并且这两层隐含层和softmax层与感知机层都有连接，如下图：
这里写图片描述
此网络结构在Chen的基础上准确度提高了大约1%。具体可以参考他们的文章Structured Training for Neural Network Transition-Based Parsing

【Hiroyasu Yamada, Yuji Matsumoto】STATISTICAL DEPENDENCY ANALYSIS WITH SUPPORT VECTOR MACHINES
【Joakim Nivre】Inductive Dependency Parsing
【Joakim Nivre】Incrementality in Deterministic Dependency Parsing
【Danqi Chen, Christopher D. Manning】A Fast and Accurate Dependency Parser using Neural Networks
【David Weiss, Chris Alberti, Michael Collins, Slav Petrov】Structured Training for Neural Network Transition-Based Parsing