排序算法详解

于 2024-01-22 18:38:26 发布
阅读量945 收藏 17
点赞数 19
分类专栏： 算法与数据结构 文章标签： 排序算法 算法 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/liu_xinLL/article/details/135755449
版权
博客提及离散数学中偏序和全序的定义，还指出若图中存在有向环，顶点无法满足拓扑次序，涉及信息技术领域的离散数学知识。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

O(n^2)
代码实现：
void select_sort( int * arr , int l , int r ) {
    for ( int i = 0, I = r - 1; i < I; i++) {
        int ind = i;
        for ( int j = i + 1; j < r ; j++) {
            if ( arr [j] < arr [ind]) ind = j;
        }
        swap( arr [i], arr [ind]);
    }
    return ;
}
O（n^2）但比选择排序略快
代码实现：
void insert_sort( int * arr , int l , int r ) {
    for ( int i = l + 1; i < r ; i++) {
        int j = i;
        while (j > l && arr [j] < arr [j - 1]) {
            swap( arr [j], arr [j - 1]);
            j--;
        }
    }
    return ;
} ;
优化：
void unguarded_insert_sort( int * arr , int l , int r ) {
    int ind = l ;
    for ( int i = l + 1; i < r ; i++) {
        if ( arr [ind] > arr [i]) ind = i;
    }
    //保证了插入排序算法的稳定性
    while (ind > l ) {
        swap( arr [ind], arr [ind - 1]);
        ind -= 1;
    }
    for ( int i = l + 1; i < r ; i++) {
        int j = i;
        //体现了无监督
        while ( arr [j] < arr [j - 1]) {
            swap( arr [j], arr [j - 1]);
            j--;
        }
    }
    return ;
}
希尔排序（分组插入排序） 
1、设计⼀个【步长】序列 
2、按照步长，对序列进⾏分组，每组采用插⼊排序 
3、直到执 ⾏ 到步长为1为 ⽌
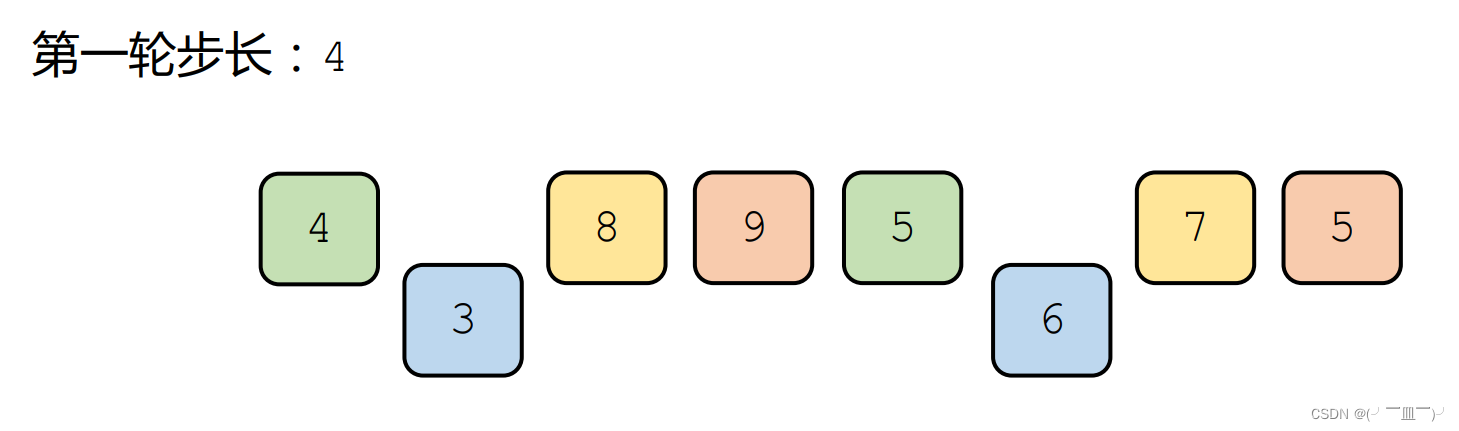
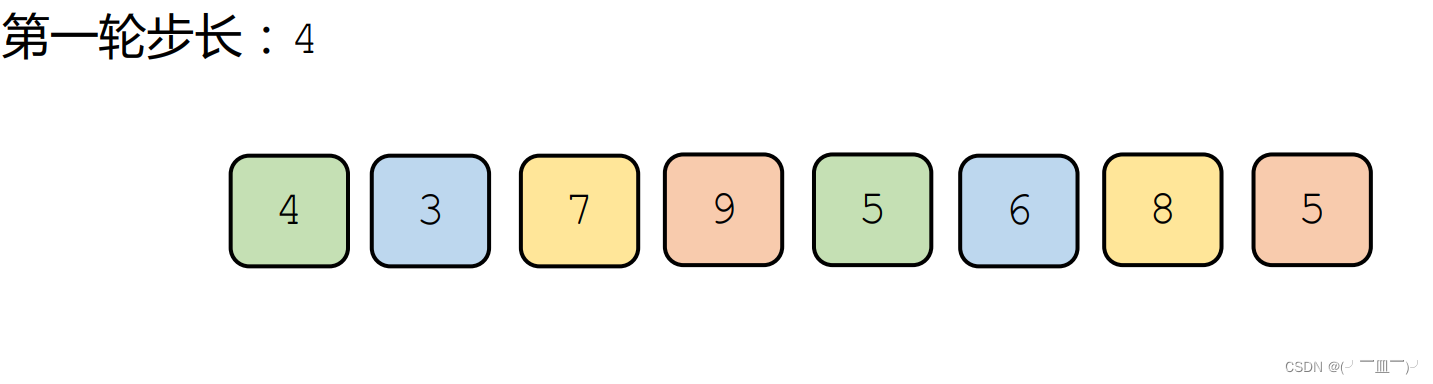
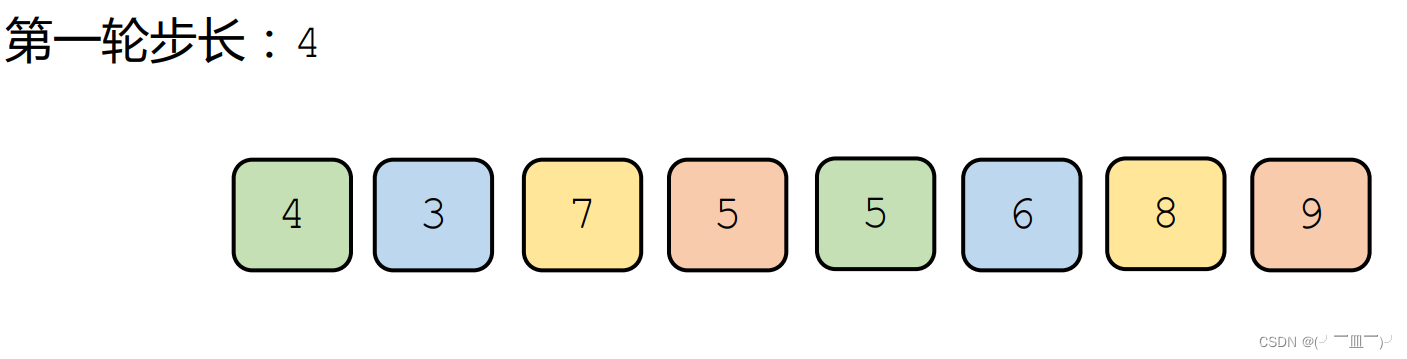
希尔排序的效率和【步长序列】紧密相关 
参考时间复杂度：O(nlogn) ~ O(n^2) 
O(n^2) 希尔增量序列：n/2、n/4、n/8、n/16 …… 
O(n^1.5) Hibbard增量序列：1、3、7 … 2k-1
代码实现：
void unguarded_insert_sort( int * arr , int l , int r , int step ) {
    int ind = l ;
    for ( int i = l + step ; i < r ; i += step ) {
        if ( arr [i] < arr [ind]) ind = i;
    }
    while (ind > l ) {
        swap ( arr [ind], arr [ind - step ]);
        ind -= step ;
    }
    for ( int i = l + 2 * step ; i < r ; i += step ) {
        int j = i;
        while ( arr [j] < arr [j - step ]) {
            swap ( arr [j], arr [j - step ]);
            j -= step ;
        }
    }
    return ;
}
void shell_sort( int * arr , int l , int r ) {
    int k = 2, n = ( r - l ), step;
    do {
        //计算步长
        step = n / k == 0 ? 1 : n / k;
        for ( int i = l , I = l + step; i < I; i++) {
            unguarded_insert_sort( arr , i, r , step);
        }
        k *= 2;
    } while (step != 1);
    return ;
}
void shell_sort_hibbard( int * arr , int l , int r ) {
    int step = 1, n = ( r - l );
    //计算步长
    while (step <= n / 2) step = step * 2 + 1;
    do {
        step /= 2;
        for ( int i = l , I = l + step; i < I; i++) {
            unguarded_insert_sort( arr , i, r , step);
        }
    } while (step > 1);
    return ;
}
冒泡排序
1、将数组分成『已排序区』和『待排序区』 
2、从头到尾扫描『待排序区』，若前面元素比后面元素⼤，则交换。 
3、每⼀轮都会将『待排序区』中最⼤的放到『已排序区』的开头 
4、直到『待排序区』没有元素为⽌
void bubble_sort( int * arr , int l , int r ) {
        for ( int i = r - 1, I = l + 1; i >= I; i--) {
               for ( int j = l ; j < i; j++) {
                       if ( arr [j] > arr [j + 1])swap( arr [j], arr [j + 1]);
              }
       }
        return ;
}
void bubble_sort_plus ( int * arr , int l , int r ) {
        for ( int i = r - 1, I = l + 1, cnt; i >= I; i--) {
              cnt = 0;
               for ( int j = l ; j < i; j++) {
                       if ( arr [j] <= arr [j + 1]) continue ;
                      swap( arr [j], arr [j + 1]);
                      cnt += 1;
              }
               if (cnt == 0) break ;
       }
        return ;
}
快速排序
时间复杂度：O(nlogn) ~ O(n2)
1.选择数组第一个数为基准值
2.选左右端为指针，移动指针，将数组分为大于基准值和小于基准值的两部分
3.由于快排属于树形结构，所以递归实现
void quick_sort( int * arr , int l , int r ) {
        if ( r - l <= 2) {
               if ( r - l <= 1) return ;
               if ( arr [ l ] > arr [ l + 1]) swap( arr [ l ], arr [ l + 1]);
               return ;
       }
        //partition
        int x = l, y = r - 1, z = arr [ l ];
        while (x < y) {
               while (x < y && z <= arr [y]) --y;
               if (x < y) arr [x++] = arr [y];
               while (x < y && arr [x] <= z) ++x;
               if (x < y) arr [y--] = arr [x];
       }
        arr [x] = z;
        //左闭右开
       quick_sort( arr , 1, x);
       quick_sort( arr , x + 1, r );
        return ;
}
//优化1
void quick_sort_v1( int * arr , int l , int r ) {
    if ( r - l <= 2) {
        if ( r - l <= 1) return ;
        if ( arr [ l ] > arr [ l + 1]) swap( arr [ l ], arr [ l + 1]);
        return ;
    }
    // partition
    int x = l , y = r - 1, z = arr [ l ];
    do {
        //减少了分区的判断操作
        while ( arr [x] < z) ++x;
        while ( arr [y] > z) --y;
        if (x <= y) {
            swap( arr [x], arr [y]);
            ++x, --y;
        }
    } while (x <= y);
    quick_sort_v1( arr , l , x);
    quick_sort_v1( arr , x, r );
    return ;
}
//三点取中法
inline int three_point_select( int a , int b , int c ) {
    if ( a > b ) swap( a , b );
    if ( a > c ) swap( a , c );
    if ( b > c ) swap( b , c );
    return b ;
}
void quick_sort_v2( int * arr , int l , int r ) {
    if ( r - l <= 2) {
        if ( r - l <= 1) return ;
        if ( arr [ l ] > arr [ l + 1]) swap( arr [ l ], arr [ l + 1]);
        return ;
    }
    // partition
    //减少树形结构的层数，减少递归调用的次数
    int x = l , y = r - 1;
    int z = three_point_select(
        arr [ l ],
        arr [ r - 1],
        arr [( l + r ) / 2]
    );
    do {
        while ( arr [x] < z) ++x;
        while ( arr [y] > z) --y;
        if (x <= y) {
            swap( arr [x], arr [y]);
            ++x, --y;
        }
    } while (x <= y);
    quick_sort_v2( arr , l , x);
    quick_sort_v2( arr , x, r );
    return ;
}
void quick_sort_v3( int * arr , int l , int r ) {
    if ( r - l <= 2) {
        if ( r - l <= 1) return ;
        if ( arr [ l ] > arr [ l + 1]) swap( arr [ l ], arr [ l + 1]);
        return ;
    }
    //单边递归法
    while ( l < r ) {
        // partition
        int x = l , y = r - 1;
        int z = three_point_select(
            arr [ l ],
            arr [ r - 1],
            arr [( l + r ) / 2]
        );
        do {
            while ( arr [x] < z) ++x;
            while ( arr [y] > z) --y;
            if (x <= y) {
                swap( arr [x], arr [y]);
                ++x, --y;
            }
        } while (x <= y);
        quick_sort_v3( arr , l , x); // left
        //右边循环实现
        l = x;
    }
    return ;
}
#define threshold 16
void unguarded_insert_sort( int * arr , int l , int r ) {
    int ind = l ;
    for ( int i = l + 1; i < r ; i++) {
        if ( arr [i] < arr [ind]) ind = i;
    }
    while (ind > l ) {
        swap( arr [ind], arr [ind - 1]);
        ind -= 1;
    }
    for ( int i = l + 1; i < r ; i++) {
        int j = i;
        while ( arr [j] < arr [j - 1]) {
            swap( arr [j], arr [j - 1]);
            j -= 1;
        }
    }
    return ;
}
void __quick_sort_v4( int * arr , int l , int r ) {
    //在阈值内采用插入排序
    while ( r - l > threshold ) {
        // partition
        int x = l , y = r - 1;
        int z = three_point_select(
            arr [ l ],
            arr [ r - 1],
            arr [( l + r ) / 2]
        );
        do {
            while ( arr [x] < z) ++x;
            while ( arr [y] > z) --y;
            if (x <= y) {
                swap( arr [x], arr [y]);
                ++x, --y;
            }
        } while (x <= y);
        __quick_sort_v4( arr , l , x); // left
        l = x;
    }
    return ;
}
void quick_sort_v4( int * arr , int l , int r ) {
    __quick_sort_v4( arr , l , r );
    unguarded_insert_sort( arr , l , r );
    return ;
}
归并排序
//保留数组上一次的归并排序结果
int *buff;
buff = ( int *)malloc( sizeof ( int ) * BIG_DATA_N );
//
void merge_sort( int * arr , int l , int r ) {
    if ( r - l <= 1) return ;
    int mid = ( l + r ) / 2;
//分区
    merge_sort( arr , l , mid);
    merge_sort( arr , mid, r );
    // merge
    int p1 = l , p2 = mid, k = 0;
    while (p1 < mid || p2 < r ) {
        if (p2 == r || (p1 < mid && arr [p1] <= arr [p2])) {
            buff[k++] = arr [p1++];
        } else {
            buff[k++] = arr [p2++];
        }
    }
//拷贝
    for ( int i = l ; i < r ; i++) arr [i] = buff[i - l ];
    return ;
}
应用：求解逆序问题（海贼oj_248）
基数排序--O(logK * n)
步骤：
1.将要排序数分为两部分，作为基数
2.分别计算相同基数的被排序数的个数，确定从哪开始排序
3.分别以基数的大小进行排序，基数相同的数相对位置不变
代码实现：
//正数的排序
void radix_sort( int * arr , int l , int r ) {
    #define K 65536
    int *cnt  = ( int *)malloc( sizeof ( int ) * K );
    int *temp = ( int *)malloc( sizeof ( int ) * ( r - l ));
    // round 1
    //将前2^16位作为基数
    memset(cnt, 0, sizeof ( int ) * K );
    for ( int i = l ; i < r ; i++) cnt[ arr [i] % K ] += 1;
    for ( int i = 1; i < K ; i++) cnt[i] += cnt[i - 1];
    for ( int i = r - 1; i >= l ; i--) temp[--cnt[ arr [i] % K ]] = arr [i];
    memcpy( arr + l , temp, sizeof ( int ) * ( r - l ));
    // round 2
    //将后2^16位作为基数
    memset(cnt, 0, sizeof ( int ) * K );
    for ( int i = l ; i < r ; i++) cnt[ arr [i] / K ] += 1;
    for ( int i = 1; i < K ; i++) cnt[i] += cnt[i - 1];
    for ( int i = r - 1; i >= l ; i--) temp[--cnt[ arr [i] / K ]] = arr [i];
    memcpy( arr + l , temp, sizeof ( int ) * ( r - l ));
    return ;
}
总结：
排序算法的稳定性：相同元素的相对位置不改变，则排序算法具有稳定性。
稳定排序：插入排序，冒泡排序，归并排序，基数排序
非稳定排序：选择排序，希尔排序，快速排序，堆排序
内部/外部排序：只可以使用内存空间/可以使用内存空间和硬盘空间，进行排序。
外部排序可以用于大数据排序。
内部排序： 插入排序，冒泡排序， 选择排序，希尔排序，快速排序，堆排序。
外部排序： 归并排序，基数排序
sort:
#include<algorithm>
sort(首指针/首迭代器，尾指针+1/尾迭代器，cmp(函数))
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
#include "0.sort_test.h"
using namespace std;
void output( int * arr , int n , const char * s = "arr" );
template < typename T >
void output( vector < T >& arr );
void test1() {
    printf( "\ntest array : \n" );
    // sort array
    int * arr = getRandData(10);
    output(arr, 10);
    //从小到大
    sort(arr, arr + 10); // [)
    output(arr, 10);
    //从大到小
    sort(arr, arr + 10, greater < int >());
    output(arr, 10);
    free(arr);
    return ;
}
void test2() {
    printf( "\ntest vector : \n" );
    // sort vector
    vector < int > arr;
    for ( int i = 0; i < 10; i++) arr.push_back(rand() % 10000);
    output(arr);
    sort(arr.begin(), arr.end());
    output(arr);
    sort(arr.begin(), arr.end(), greater < int >());
    output(arr);
    return ;
}
struct Data {
    int x, y;
};
ostream & operator<< ( ostream & out , const Data & d ) {
    out << "(" << d .x << ", " << d .y << ")" ;
    return out ;
}
bool cmp( const Data & a , const Data & b ) {
    //先按x从小到大排
    if ( a .x != b .x) return a .x < b .x;
    //再按y从大到小排
    return a .y > b .y;
}
void test3() {
    printf( "\ntest my data structure : \n" );
    vector < Data > arr;
    for ( int i = 0; i < 10; i++) {
        Data d;
        d.x = rand() % 10, d.y = rand() % 10;
        arr.push_back(d);
    }
    output(arr);
    sort(arr.begin(), arr.end(), cmp);
    output(arr);
    return ;
}
void test4() {
    //不改变原数组数据的排序--下标排序
    printf( "\ntest sort ind : \n" );
    int * arr = getRandData(10);
    int * ind = getRandData(10);
    for ( int i = 0; i < 10; i++) ind[i] = i;
    output(arr, 10);
    //表达式
    sort(ind, ind + 10, [&]( int i , int j ) -> bool {
        return arr[ i ] < arr[ j ];
        });
    output(arr, 10);
    output(ind, 10, "ind" );
    return ;
}
int main() {
    test1();
    test2();
    test3();
    test4();
    return 0;
}
template < typename T >
void output( vector < T >& arr ) {
    printf( "arr[%lu] = " , arr .size());
    for ( int i = 0; i < arr .size(); i++) {
        cout << arr [i] << " " ;
    }
    printf( "\n" );
    return ;
}
void output( int * arr , int n , const char * s ) {
    printf( "%s[%d] = " , s , n );
    for ( int i = 0; i < n ; i++) {
        printf( "%d " , arr [i]);
    }
    printf( "\n" );
    return ;
}
拓扑排序：
有向无环图：指的是一个无回路的有向图。如果有一个非有向无环图，且A点出发向B经C可回到A，形成一个环。将从C到A的边方向改为从A到C，则变成有向无环图。 一个有向无环图至少有一个入度为0的顶点和一个出度为0的顶点。
对一个 有向无环图 ( Directed Acyclic Graph 简称 DAG ) G 进行拓扑排序，是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v ，若边 < u , v > ∈ E ( G )，则 u 在线性序列中出现在 v 之前。通常，这样的线性序列称为满足拓扑次序 ( Topological Order ) 的序列，简称拓扑序列。 由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。
ps:
  • 离散数学中关于偏序和全序的定义：
         若集合X上的关系是R,且R是自反的、反对称的和传递的，则称R是集合X上的偏序关系。 设R是集合X上的偏序（Partial Order）,如果对每个x,y属于X必有xRy 或 yRx，则称R是集合X上的全序关系。 比较简单的理解：偏序是指集合中只有部分成员可以比较，全序是指集合中所有的成员之间均可以比较。
  • 若图中存在有向环，则不可能使顶点满足拓扑次序。
作用： 图形的顶点可以表示要执行的任务（递归函数），并且边可以表示一个任务 （递归函数） 必须在另一个任务 （递归函数） 之前执行的约束；在这个应用中，拓扑排序只是一个有效的任务 （递归函数调用） 顺序，以此实现递归转非递归
拓扑排序实现过程：
1.找出入度为0的节点，入队
2.处理当前队首节点，将队首节点有向边指向的所有节点的入度减一，并将入度为一的节点入队（bfs）
3.队首元素出队，处理新的队首元素
4.循环至队为空
5.出队序列就为拓扑序列
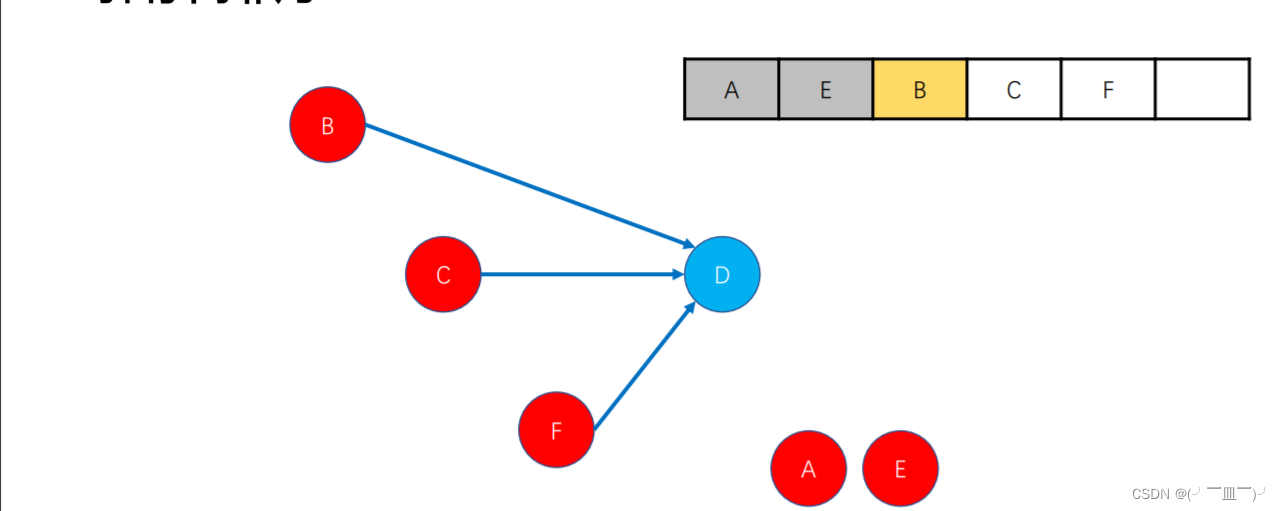
代码演示：
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;
#define MAX_N 2000
//入度
int indeg[ MAX_N + 5] = {0};
//路径
vector < vector < int >> g( MAX_N + 5);
//拓扑序列
int ans[ MAX_N + 5], cnt = 0;
int main() {
    int n, m;
    cin >> n >> m;
    for ( int i = 0, a, b; i < m; i++) {
        cin >> a >> b;
        indeg[b] += 1;
        g [ a ] .push_back(b);
    }
    set < int > q;
    for ( int i = 1; i <= n; i++) {
        if (indeg[i] == 0) q.insert(i);
    }
    while (q.size() > 0) {
        int now = * q.begin(); // top()
        ans[cnt++] = now;
        q.erase(q.begin());   // pop()
        //-------
        for ( int i = 0, I = g [ now ] .size(); i < I; i++) {
            int t = g [ now ][ i ] ;
            indeg[t] -= 1;
            if (indeg[t] == 0) {
                q.insert(t);
            }
        }
        //-------
    }
    for ( int i = 0; i < n; i++) {
        if (i) cout << " " ;
        cout << ans[i];
    }
    cout << endl;
    return 0;
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值