无线通信中的分式规划（Fractional Programming）与Matlab实现

伽蓝雨不停

已于 2024-01-04 10:49:59 修改

阅读量1.7k

点赞数 10

分类专栏：无线通信仿真文章标签： matlab 开发语言 5G 论文阅读算法

于 2023-08-02 14:03:34 首次发布

本文链接：https://blog.csdn.net/liujun19930425/article/details/132059080

版权

无线通信仿真专栏收录该内容

6 篇文章 90 订阅

订阅专栏

引言

本文主要介绍Shen Kaiming老师的论文《Fractional programming for communication systems—Part I: Power control and beamforming》所介绍的无线通信中遇到的多项分式规划求解方法。

在多用户（multi user）无线通信的系统优化设计中，经过遇到以下两类优化问题：

1. 最大化系统和速率（Sum Rate）问题

$\max { }\sum_{i=1}^{n}{\log\left( 1+\gamma_i \right)}$

$\gamma_i$ 是 $i$ 用户的SINR。目标函数对多个对数函数求和，优化变量是SINR的自变量。

2. 最大化系统能量效率（Energy Efficiency）问题

$\max \frac{\sum_{i=1}^{N}{R_i\left( p \right)}}{\sum_{i=1}^{N}{p}+P_{\text{on}}} \\ s.t. \sum_{i=1}^{N}{p}\leq P_{\max}$

问题1可以通过[1]中所提出的拉格朗日对偶变换（Lagrangian dual transform）转化为一个多项分式规划问题；问题2是一个分式规划问题。类似于以上多项对数和或者目标函数含有多项分式和的问题，都可以可以通过[2]中所提出的二次变换（Quadratic transform）来解决。该方法是无线通信优化论文中较常见的将非凸优化问题转化为凸优化问题的方法，在RIS的优化中也有见到，因此在本文中介绍该转化方法的核心思想和功率控制部分的matlab代码（波束成形和能效能量效率问题的部分后续补上），供大家参考，如果有不清楚或者文中理解不准确的地方，希望大家留言或私信交流。

传统分式规划方法

传统的分式规划问题多集中于单项分式规划问题，即目标函数中只含有一个分式，而多项分式规划问题是多个分式求和的形式，下面简要介绍传统的分式规划问题求解方法。单项分式规划问题可表示为以下的通用形式

$\max \frac{A\left( \mathbf{x} \right)}{B\left( \mathbf{x} \right)}\\ \text{s.t. }\mathbf{x}\in\mathcal{X}. \\$

其中 $A\left( \mathbf{x} \right):\mathbb{R}^d\rightarrow\mathbb{R}_+$ 是值域为非负的函数， $B\left( \mathbf{x} \right):\mathbb{R}^d\rightarrow\mathbb{R}_{++}$ 是值域为正的函数。

Charnes-Cooper变换

引入两个辅助变量：

$z=\frac{1}{B\left( \mathbf{x} \right)},\mathbf{q}=\frac{\mathbf{x}}{B(\mathbf{x})}\\$

因此通用形式的单项分式规划问题可以写成以下形式

$\max_{z,\mathbf{q}} zA\left( \frac{\mathbf{q} }{z} \right)\\ \text{s.t. } zB\left( \frac{\mathbf{q} }{z} \right) \leq 1 \\ z\in\mathcal{Z} \\ \mathbf{q}\in\mathcal{Q} \\$

很明显带入辅助变量，目标函数不变， $z$ 和 $\mathbf{q}$ 的定义域根据 $\mathbf{x}$ 的定义域计算，因此该方法较为麻烦， $z$ 和 $\mathbf{q}$ 二者相互迭代优化，且很难推广到求解多项分式规划问题。

Dinkelbach's变换

该方法思路简单，主要是将分式规划问题变换为差的形式，如下所示：

$\max_\mathbf{x} A\left( \mathbf{x} \right) - y{B\left( \mathbf{x} \right)}\\ \text{s.t. }\mathbf{x}\in\mathcal{X}. \\$

其中 $y\left[ t+1 \right]=\frac{A\left( \mathbf{x}\left[ t \right] \right)}{B\left( \mathbf{x}\left[ t \right] \right)}$ ，两个变量相互迭代更新，而且不用重新计算辅助变量的定义域，但是目标函数的值和原目标函数的值不同，因此无法应用到多项分式规划中。

二次变换

以上单项分式规划都难以推广到多项分式规划中，主要是变化后的目标函数值和原目标函数值发生了变化，当多项分式规划时，对单项分式的值影响不同，导致最优解与原问题不同。因此转化后的目标函数需要满足以下四点条件：

解耦性：新的目标函数的形式需要满足 $g\left( \mathbf{x},y \right)=f\left( A\left( \mathbf{x} \right) \right)q_1\left( y \right)- h\left( B\left( \mathbf{x} \right) \right)q_2\left( y \right)$ ，比较容易理解，需要将分子和分母解耦为差的形式 ;
解的等价性： $A\left( \mathbf{x} \right)/B\left( \mathbf{x} \right)$ 和所设计的函数 $g\left( \mathbf{x},y \right)$ 的最优解 $\mathbf{x}^\star$ 在 $y$ 等于某一个值时相等；
目标值的的等价性： $A\left( \mathbf{x} \right)/B\left( \mathbf{x} \right)$ 和所设计的函数 $g\left( \mathbf{x},y \right)$ 的目标值在 $y$ 等于某一个值时，相等；
凹性：所设计的函数 $g\left( \mathbf{x},y \right)$ 当 $\mathbf{x}$ 固定时，关于 $y$ 是凹函数，即 $\partial^2g/\partial y^2\leq0$ 。

因此可设计如下的变换函数，即二次变换（Quadratic transform）：

$g\left( \mathbf{x},y \right)=2y\sqrt{A\left( \mathbf{x} \right)}-y^2B\left( \mathbf{x} \right)$

利用二次变换可以解决（但不限于）以下三类分项分式规划问题：

1) 对于以下的多项分式规划问题：

$\max_\mathbf{x} \sum_{m=1}^{M}\frac{A_m\left( \mathbf{x} \right)}{B_m\left( \mathbf{x} \right)}\\ \text{s.t. }\mathbf{x}\in\mathcal{X}. \\$

通过二次变换，可以等价地变换为如下形式：

$\max_\mathbf{x,y} \sum_{m=1}^{M}\left( 2y_m\sqrt{A_m\left( \mathbf{x} \right)}-y_m^2 B_m\left( \mathbf{x} \right)\right)\\ \text{s.t. }\mathbf{x}\in\mathcal{X}, y_m\in\mathbb{R} \\$

2) 给定一系列的非减函数 $f_m\left( \cdot \right)$ 和比值 $A_m\left( \mathbf{x} \right)/B_m\left( \mathbf{x} \right), m=1,\dots,M$ ，那么多项比例函数的和（sum-of-functions-ratio）问题：

$\max_\mathbf{x} \sum_{m=1}^{M}f_m\left(\frac{A_m\left( \mathbf{x} \right)}{B_m\left( \mathbf{x} \right)}\right)\\ \text{s.t. }\mathbf{x}\in\mathcal{X}. \\$

通过二次变换，可以等价地变换为如下形式：

$\max_\mathbf{x,y} \sum_{m=1}^{M}f_m\left( 2y_m\sqrt{A_m\left( \mathbf{x} \right)}-y_m^2 B_m\left( \mathbf{x} \right)\right)\\ \text{s.t. }\mathbf{x}\in\mathcal{X}, y_m\in\mathbb{R} \\$

3) 对于最大最小分式（max-min-ratio）问题：

$\max_\mathbf{x} \min_{m} \left\{ \frac{A_m\left( \mathbf{x} \right)}{B_m\left( \mathbf{x} \right)} \right\}\\ \text{s.t. } \mathbf{x}\in\mathcal{X} \\$

等价于

$\max_{\mathbf{x},\mathbf{y},z} ~~z\\ \text{s.t.} ~~\mathbf{x}\in \mathcal{X}, y_m\in\mathbb{R}, z\in\mathbb{R}\\ 2y_m\sqrt{A_m\left( \mathbf{x} \right)}-y_m^2B_m\left( \mathbf{x} \right)\geq z, \forall m. \\$

以上的变换都比较容易理解，具体证明可以仔细阅读文献[2]的相关内容。为解决无线通信中的相关问题，二次变换也可以拓展到向量和复数域。

Concave-Convex分式规划

以上的变换对于分式的分子只有非负而分母为正的限制条件，但如果需要进一步使得经过二次变换后的问题容易求解，或者说当 $y$ 固定时候是凸的，则需要满足

分式的分子是凹函数
分母是凸函数
约束集合 $\mathcal{X}$ 是凸集

以上条件较为容易理解，当 $y$ 固定时，二次变换后的函数 $g\left( \mathbf{x},y \right)$ 中 $A_m\left( \mathbf{x} \right)$ 前是正号，对于最大化问题， $A_m\left( \mathbf{x} \right)$ 需要满足是凹函数的条件，而 $B_m\left( \mathbf{x} \right)$ 前是负号，因此需要 $B_m\left( \mathbf{x} \right)$ 满足是凸函数的条件，此时 $g\left( \mathbf{x},y \right)$ 整体是凹函数，可以利用CVX直接求解。

因此这种比较容易求解的分式规划问题称为Concave-Convex分式规划问题，在无线通信中也比较容易满足以上三个条件。

Concave-Convex分式规划的迭代式求解方法

1）当 $\mathbf{x}$ 固定时， $g\left( \mathbf{x},y \right)$ 对 $y$ 求偏导，并令偏导数等于0： $\partial g\left( \mathbf{x},y \right)/\partial y =0$ ，可以得到最优 $y_m$ 的闭式解为：

$y_m^\star = \frac{\sqrt{A\left( \mathbf{x} \right)}}{B\left( \mathbf{x} \right)}, \forall m=1,\dots,M. \\$

2) 当 $y$ 固定时， $g\left( \mathbf{x},y \right)$ 关于 $\mathbf{x}$ 是凹函数，可以通过凸优化工具箱求解。

步骤1）2）相互迭代，直至收敛。

实例：无线通信中的功率控制问题

功率控制问题

多用户多小区蜂窝无线通信系统中，功率控制问题是最为常见的一类问题，一般是在最大功率的约束下，通过控制不同基站的发射功率而达到系统的和速率最大化，尽量减小小区间干扰的影响，各用户的速率可以表示为：

$R_i=\log\left( 1+\frac{\left| h_{i,i} \right|^2p_i}{\sum_{j\ne i}{h_{i,j}p_j}+\sigma^2} \right) \\$

其中 $h_{i,j}$ 表示基站 $j$ 到用户 $i$ 的信道， $p_i$ 表示第 $i$ 各基站的发射功率，假设每个小区中只存在一个单天线的用户。加权速率和最大化函数为：

$f\left( \mathbf{p} \right)=\sum_{i\in\mathcal{B}}{w_iR_i}\\$

功率控制问题：

$\max_{\mathbf{p}}~~ f\left( \mathbf{p} \right) \\ \text{s.t. } ~~0\le p_i \le P_{\max}, \forall i\in\mathcal{B} \\$

由于 $R_i$ 中的SINR是分式形式，所以功率控制问题是一个典型的多项比例函数的和问题， $\log\left( \cdot \right)$ 是一个非减函数，SINR的分子和分母都既是凸函数又是凹函数，可以利用Concave-Convex分式规划的方法求解。

1）直接式求解方法

对 $f\left( \mathbf{p} \right)$ 进行二次变换，可以得到：

$f^{\mathsf{DIR}}\left( \mathbf{p},\mathbf{y} \right)=\sum_{i\in\mathcal{B}}{w_i\log\left( 1+2y_i\sqrt{\left| h_{i,i} \right|^2p_i}-y_i^2\left( \sum_{j\ne i}{\left| h_{i,j} \right|^2p_j}+\sigma^2 \right) \right)} \\$

优化问题可以变换为

$\max_{\mathbf{p},\mathbf{y}}~~ f^{\mathsf{DIR}}\left( \mathbf{p},\mathbf{y} \right) \\ \text{s.t.}~~~~~~~ 0\le p_i \le P_{\max}, \forall i \in \mathcal{B} \\ ~~~~~~~~~~~~y_i\in\mathbb{R}, \forall i \in \mathcal{B} \\$

固定 $\mathbf{p}$ 时，最优 $y_i$ 的闭式解为

$y_i^\star = \frac{\sqrt{\left| h_{i,i} \right|^2p_i}}{\sum_{j\ne i}{h_{i,j}p_j}+\sigma^2} \\$

固定 $\mathbf{y}$ 时，变换后的问题是一个凸优化问题，可以根据以下的伪代码迭代求解

2）闭式解方法

该方法利用[1]中给出的拉格朗日对偶变换（Lagrangian dual transform）（这个变换在以后有时间再详细介绍，在此不再赘述，不清楚的可以阅读文献[1]），通过引入辅助变量的方法解决掉分式外层的对数函数，拉格朗日对偶变换后会出现新的不含有对数函数的分式，可以通过上文提到的二次变换处理。首先对 $f\left( \mathbf{p} \right)$ 进行拉格朗日对偶变换：

$f_1^{\mathsf{CF}}(\mathbf{p}, \gamma)=\sum_{i \in \mathcal{B}} w_i \log ( \left.1+\gamma_i\right)-\sum_{i \in \mathcal{B}} w_i \gamma_i +\sum_{i \in \mathcal{B}} \frac{w_i\left(1+\gamma_i\right)\left|h_{i, i}\right|^2 p_i}{\sum_{j \in \mathcal{B}}\left|h_{i, j}\right|^2 p_j+\sigma^2} \\$

论文[2]中对 $f_1^{\mathsf{CF}}(\mathbf{p}, \gamma)$ 关于 $\gamma$ 求偏导， $\partial f_1^{\mathsf{CF}}(\mathbf{p}, \gamma)/\partial \gamma_i=0$ ，得到最优解

$\gamma_i = \frac{\left| h_{i,i} \right|^2p_i}{\sum_{j\ne i}{h_{i,j}p_j}+\sigma^2} \\$

但是根据这里对 $\gamma_i$ 求导的得到的最优解进行迭代，我自己根据论文所给的伪代码仿真始终无法收敛，会产生振荡，甚至系统和速率会逐渐减小，所以在拉格朗日对偶变换就直接对 $\gamma_i$ 求偏导表示存疑，而且这样迭代更新的 $\gamma_i$ 和后面进行二次变换后的辅助变量 $y_i$ 无法产生关系，我自己理解应该是在拉格朗日对偶变换和二次变换后再对 $\gamma_i$ 求偏导。

对 $f_1^{\mathsf{CF}}(\mathbf{p}, \gamma)$ 的分式部分进行二次变换可以得到

$f_2^{\mathsf{CF}}(\mathbf{p}, \gamma,\mathbf{y})=\sum_{i \in \mathcal{B}} w_i \log ( \left.1+\gamma_i\right)-\sum_{i \in \mathcal{B}} w_i \gamma_i +\sum_{i \in \mathcal{B}}{2y_i\sqrt{w_i\left(1+\gamma_i\right)\left|h_{i, i}\right|^2 p_i}}-\sum_{i \in \mathcal{B}}{y_i^2\left(\sum_{j \in \mathcal{B}}\left|h_{i, j}\right|^2 p_j+\sigma^2 \right)} \\$

对 $f_2^{\mathsf{CF}}(\mathbf{p}, \gamma,\mathbf{y})$ 关于 $\gamma$ 求偏导， $\partial f_2^{\mathsf{CF}}(\mathbf{p}, \gamma,\mathbf{y})/\partial \gamma_i=0$ ，得到最优解

$\gamma_i^\star = \frac{y_i^2\left| h_{i,i} \right|^2p_i+\sqrt{\left( y_i^2\left| h_{i,i} \right|^2p_i \right)^2+4y_i^2\left| h_{i,i} \right|^2p_i}}{2}\\$

同理，可以得到最优解 $p_i^\star$ 和 $y_i^\star$

$p_i^{\star}=\min \left\{P_{\max }, \frac{y_i^2 w_i\left(1+\gamma_i\right)\left|h_{i, i}\right|^2}{\left(\sum_{j \in \mathcal{B}} y_j^2\left|h_{j, i}\right|^2\right)^2}\right\}, y_i^{\star}=\frac{\sqrt{w_i\left(1+\gamma_i\right)\left|h_{i, i}\right|^2 p_i}}{\sum_{j \in \mathcal{B}}\left|h_{i, j}\right|^2 p_j+\sigma^2}, \forall i \in \mathcal{B} \\$

论文中给出的闭式方法求解的伪代码如下：

但是根据该伪代码和公式(42)的迭代方法，大多数情况下收敛曲线振荡无法收敛，对照公式调试很久也无法得到论文中呈现的效果，不清楚我自己理解是否有问题，如果理解有错误，欢迎评论和私信交流。因此我在二次变换后，再对 $\gamma_i$ 求偏导，然后根据以下的方式进行迭代更新，才得到较好的效果：

$\mathbf{y}\rightarrow\mathbf{p}\rightarrow\gamma\rightarrow\mathbf{p} \\$

仿真

仿真环境

论文中设置的是7个相邻的正六边形蜂窝小区，每个蜂窝小区中有且仅有一个用户，在7个小区中随机撒点得到以下用户位置

仿真结果

复现得到的结果：

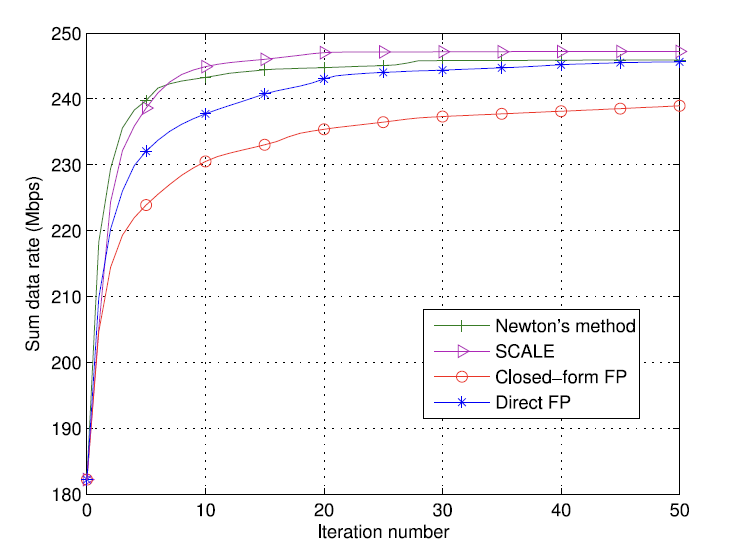
复现代码在文章标题下方下载！！

参考文献

[1] Shen K, Yu W. Fractional programming for communication systems—Part II: Uplink scheduling via matching[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2631-2644.

[2] Shen K, Yu W. Fractional programming for communication systems—Part I: Power control and beamforming[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2616-2630.

总结

二次变换和拉格朗日对偶变换在处理多项分式规划问题，高效且容易理解，但是仿真复现时，感觉收敛速度没有论文给出的快，特别是闭式解方法，若复现代码有问题，欢迎大家指出。

伽蓝雨不停

关注

10
点赞
踩
48

收藏

觉得还不错? 一键收藏
打赏
13
评论
无线通信中的分式规划（Fractional Programming）与Matlab实现

二次变换和拉格朗日对偶变换在处理多项分式规划问题，高效且容易理解，但是仿真复现时，感觉收敛速度没有论文给出的快，特别是闭式解方法，若复现代码有问题，欢迎大家指出。
复制链接

扫一扫