计算摄影-相机模型（针孔相机模型）

迷途小牛马

已于 2023-03-30 14:08:10 修改

阅读量277

点赞数

文章标签：数码相机计算机视觉 opencv 人工智能

于 2023-03-29 16:36:24 首次发布

本文链接：https://blog.csdn.net/liulibo1/article/details/129836949

版权

我们在图像中，一个像素P的坐标可以描述为(u,v),那么在真实世界中，便有一个点 $P_w(X_w,Y_w,Z_w)$ 与它对应。那么怎么它们之间存在什么样的数学关系呢？而表示它们之间的相互关系便是相机模型的研究内容。

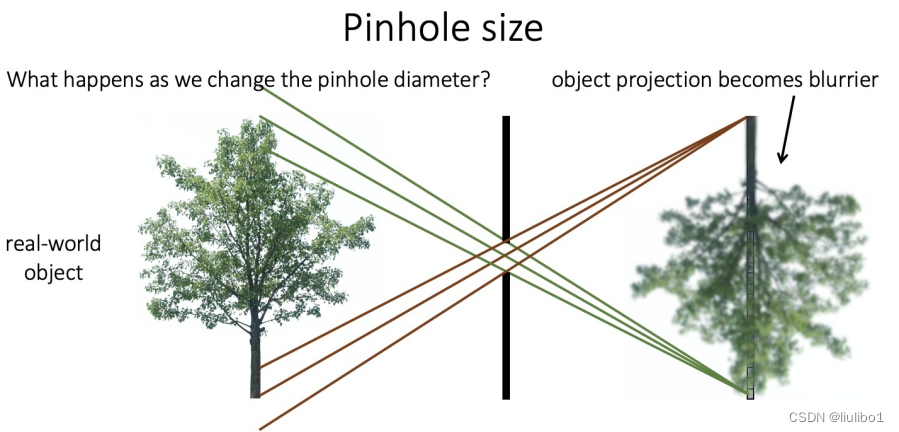
在描述这个过程之前，我们先看一下针孔相机的成像过程吧。在针孔相机模型中，如下图所示，空间中的物体通光的直射将物体的倒影反映在成像平面上。在这个过程中，物体的反射光线经过小孔，反射到成像平面。在实际的相机中，这个小孔便是透镜，而成像平面则是成像传感器（CCD or CMOS）。

那么，在这个过程中，三维空间中的一个点 $P_w$ 的坐标经过了空间坐标系-相机坐标系-成像平面坐标系-图像坐标系这几次坐标系转换成这个点在图像中的位置(u,v)。下面，我们来回顾这个过程。那么第一步便是空间坐标系到相机坐标系的转换。在这里，我们假设三维空间存在一个点 $P_w$ ，它在空间坐标系下的位置为 $(X_w,Y_w,Z_w)$ 。对应的，如果我们把它转为以相机光心（即小孔中心）为原点的相机坐标系，其坐标我们假设为 $P_w(X_c,Y_c,Z_c)$ 。这个过程可以表示为：

$P_c=RP_w+T$ （1)

其中，R为旋转矩阵，T为平移矩阵。上述过程通俗来讲，可以理解为将空间坐标系的原点通过旋转和平移转到相机表坐标系的原点。那么，为了更加方便的计算相关参数，我们也可以公式1用q齐次坐标表示，即：

$\begin{pmatrix} X_c \\ Y_c\\ Z_c\\ 1\\ \end{pmatrix}=\begin{pmatrix} R _{3\times3}&T_{3\times1} \\ 0^T & 1& \end{pmatrix} \begin{pmatrix} X_w \\ Y_w\\ Z_w\\ 1\\ \end{pmatrix}$ (2)

那么，上式 $R_{3\times3}$ 和 $T_{3\times1}$ 便是旋转矩阵和平移矩阵，它们被称为相机的外参数。那么如果从相机坐标系转为成像平面坐标系呢。这个过程分为两步，第一步我们需要求点 $P_c$ 在成像平面上的对应点 $P'$ 在相机坐标系下的坐标。第二部则是将这个坐标转换为以成像平面中心为原点的成像平面坐标系下的坐标 $P_i$ 。首先第一步，因为 $P_c$ 和 $P_i$ 成相似三角形关系，所以我们有：

$\frac{f}{Z_c}=\frac{X'}{X_c}=\frac{Y'}{Y_c}$ (3)

上式中，f为焦距(即光心到成像平面的距离)。那么我们可以得到下列公式：

$X'_c=f\frac{X_c}{Z_c} \\ Y'_c=f\frac{Y_c}{Z_c}$ (4)

那么，因为成像平面是一个二维坐标系，P点在成像平面坐标系上的Z=0,而X,Y则不动，所以：

$\begin{pmatrix} X_i\\ Y_i\\ 1\\ \end{pmatrix}= \begin{pmatrix} \frac{f}{Z_c}&0&0\\ 0&\frac{f}{Z_c}&0\\ 0&0&\frac{f}{Z_c} \end{pmatrix} \begin{pmatrix} X_c\\ Y_c\\ Z_c\\ \end{pmatrix}$ (5)

而成像平面坐标系和图像坐标系不一样，因为成像平面坐标系以成像平面中心为原心，而图像坐标系以左上角为原心，所以在这里我们需要做一个平移，而成像平面坐标系和图像坐标系量纲不一样，所以还需要做一个单位的换算。所以有：

$u=X_i*K_u+u_0 \\ v=Y_i*K_v+v_0$ (6)

也可以写成：

$\begin{pmatrix} u\\ v\\ 1\\ \end{pmatrix}= \begin{pmatrix} k_u&0&u_0\\ 0&k_v&v_0\\ 0&0&1\\ \end{pmatrix} \begin{pmatrix} X_i\\ Y_i\\ 1\\ \end{pmatrix}$ (7)

上式中：R和T为外参数，公式5和公式7可以合并，得到：

$\begin{pmatrix} u\\ v\\ 1\\ \end{pmatrix}= \begin{pmatrix} k_u&0&u_0\\ 0&k_v&v_0\\ 0&0&1\\ \end{pmatrix} \begin{pmatrix} \frac{f}{Z_c}&0&0\\ 0&\frac{f}{Z_c}&0\\ 0&0&\frac{f}{Z_c} \end{pmatrix} \begin{pmatrix} X_c\\ Y_c\\ Z_c\\ \end{pmatrix}$ （8）