《算法导论》笔记－－霍夫曼（Huffman）树构造

最新推荐文章于 2023-12-21 09:36:53 发布

liyiwen007

最新推荐文章于 2023-12-21 09:36:53 发布

阅读量314

点赞数

分类专栏：算法笔记文章标签：算法 C C++ C# F#

算法笔记专栏收录该内容

8 篇文章 0 订阅

订阅专栏

　　Huffman Code是应用很广泛的一种文本压缩编码方式。它的原理就是用不等长的编码来表示不同出现频率的字符。出现频率高的字符，就用比较短的编码来表示，出现频率低的，就是较长的编码来表示。如下表：

压缩效果表

　　图中是一个文件中出现的字符（abcdeft）以及相应的出现频率。如果使用等长编码方式，则每个字符都要用三位来表示，总的长度就是300个bit，如果用变长码来表示，则总长度为224个bit。（对于出现频率最高的a，我们就用一个0来表示它，这样，可以节省很多空间）。Huffman编码的压缩比通常都在20%－90%。

　　Huffman编码是一种前缀编码方式，所谓前缀编码，即，在编码集合中，没有任何一个编码是另一个编码的前缀。例如，用0来表示a，用10表示b，那么a的编码就不是b的编码的前缀部分。（其实把这种编码叫"前缀编码"实在是别扭，意思刚好相反了。不过《算法导论》一书也提出这种说法，"前缀编码"已经是一个通用的叫法了，所以只好一直沿用下去）

一个字符集合的最优压缩编码方案总是可以用前缀编码表示出来。前缀编码最大的好处就是没有二义性，当我们顺序读取编码文件时，只要有编码与字符匹配，就可以直接把读出来的数据翻译成相应的字符，然后再继续后面的解码。因为前缀编码决定了一个已经匹配的编码，决不可能是另一个编码的一部分，所以可以直接确定对应的字符是什么。

　　使用Huffman编码的时候，一般要生成对应文本的编码集合（Huffman树），然后再将文本的每个字符相应都转成压缩码。解码时也要依赖于对应的Huffman树，Huffman树是满二叉树（即除了叶节点之外，内部节点都有两个子节点）。如上面图中的字符以及出现频率来讲，其中的一种Huffman树可能如下图所示：

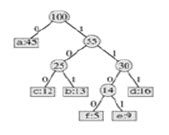
Huffman树例子

　　在解码时，先获取相应的压缩码，然后每次取一位，从树部开始查找，如果取出的位是0，就向左子节点移动，如果取出的位是1，则向右子节点移动，然后再取下一位，一直到叶节点为止。每个叶节点都是一个相应的字符。由于Huffman编码是前缀编码，所以到达叶节点时可以确定对应这个压缩码的字符就是当前所在的叶节点了。然后再取后面的压缩码，继续前面过程，最终就可以将整个文件都解码出来。

Huffman树的构造：

　　Huffman树的构造可以采用贪婪算法。用贪婪算法解决的问题，一般要满足两个条件：

1. 存在贪婪选择
2. 存在最优子结构

　　Huffman树构造问题对应的，有这样的性质（这里只阐述性质，并不进行证明了，具体的证明可以参考《算法导论》16.3节，比较详细了）：

1. 对于一字符的集合所构造的Huffman树中，频率最低的两个字符对应的节点x和y，是最优树从节点开始的最大路径长度，且x和y或为子节点。这也就意味着，频率最低的两个字符对应的编码是等长的（在压缩编码中也是最长的），而且它们之间只有最后一个bit是不同的。这一性质，表明Huffman树构造问题，是存在贪婪选择性质的。
2. 对于一个字符集C，c是C中的元素，f[c]表示字符c的出现频率。x和y是字符集C中最低频率的两个字符。如果将x和y节点去掉，换一个新节点z，且使得f[z] = f[x] + f[y]，并令，字符集C'表示这样的集合{c，c属于C－{x,y}+z}。用树T'对应字符集C'的最优编码树。那么，将T'的叶节点z去掉，并将一个包含x、y为子节点的新内节点放在z的位置，那么，得到的树T就是字符集C的一棵最优编码树。这一性质表示Huffman构造问题也存在最优子结构。

　　这样，Huffman树的构造问题就可以用贪婪算法来解决了。附件中是相应的代码。对于本文开头图中提到的例子，构造过程将如下图所示：

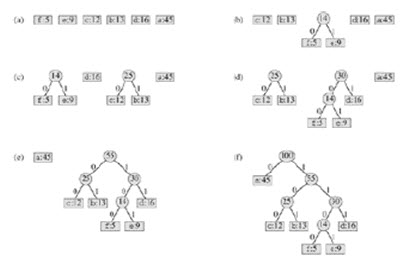
Huffman树构造

代码如下：

# 仅仅模拟了最小优先级队列的功能，并未用最小堆来实作
class MinPriorityQ:
    def __init__(self):
        self.heaplist = []
    def Dequeue(self):
        minObj = self.heaplist[0]
        idxMin = 0
        for o in self.heaplist:
            if o.comFun(minObj) < 0: 
                minObj = o
                idxMin = self.heaplist.index(o)       
        del self.heaplist[idxMin]
        return minObj
    def Insert(self, objectIn):
        self.heaplist.append(objectIn)
    def Empty(self):
        return len(self.heaplist) == 0

# Huffman树上的每个节点
class HuffmanTreeNode:
    def __init__(self, freq, char):
        self.key = freq   # 存储字符的频率
        self.char = char  # 存储字符本身
        self.left = 0     # 左子节点
        self.right = 0    # 右子节点
    def comFun(self, OtherNode): # 比如树节点，是以字符出现的频率为key来进行的
        if self.key > OtherNode.key:
            return 1
        elif self.key == OtherNode.key:
            return 0
        else:
            return -1

# 生成一树Huffman树。
def MakeHuffmanTree(charList, freList):
    num = len(charList)
    minQ = MinPriorityQ()
    # 将所有字符以及出现频率生成相应的树节点，插入到以频率为key的
    # 最小优先级队列中去
    for i in range(0, num): 
        node = HuffmanTreeNode(freList[i], charList[i])
        minQ.Insert(node)
    for i in range(0, num - 1):
        # 最出优先级最低的两个节点
        x = minQ.Dequeue()   
        y = minQ.Dequeue()
        # 用取出的两个节点的频率和作为新节点的频率
        z = HuffmanTreeNode(x.key + y.key, 0)
        # 取出的两个节点作为新节点的左右子节点
        z.left = x
        z.right = y
        minQ.Insert(z)  # 将新节点插入到队列中
    return minQ.Dequeue()    


#-----------------------------------------------
# 以下程序仅用于测试
def PrintHuffmanTree(ht):
    code = []
    Traval(code, ht)

def Traval(code, root, dir='3'):
    if not dir == '3':
        code.append(dir)

    if not root.char == 0:
        print root.char, " : ", "".join(code)
    else:
        Traval(code, root.left, '0')
        code.pop()
        Traval(code, root.right, '1')
        code.pop()
    

if __name__ == '__main__':
    charList = ['a', 'b', 'c', 'd', 'e', 'f', 'g']
    freqList = [ 2,  5,   9,    3,   40,  6,  10 ]
    TreeTop = MakeHuffmanTree(charList, freqList)
    PrintHuffmanTree(TreeTop)