前言
文中算法公式摘自《捷联惯导算法与组合导航原理》(严恭敏、翁浚 编著)、《惯性导航》(秦永元 编著),其他理解仅代表个人观点。本文对捷联惯导算法使用Matlab进行简单实现,不包含算法理解。
一、捷联惯导算法实现内容
已知初始位置和加速度计比力、陀螺仪角增量(即很短测量时间段内各个轴向速度和角度变化)推算出整个过程中姿态(俯仰角 、横滚角 、航向角 )、速度、位置(纬度 、经度 、高度 )信息。
二、用到的参数

三、捷联惯导更新算法
1.姿态更新算法
1.1、姿态更新算法中用到的是姿态更新矩阵进行更新,首先将姿态角转化为姿态更新矩阵

程序实现
function [ Mat ] = Att2Mat_sins( att )
%姿态角转化为姿态矩阵
C_1=[ 1 0 0;
0 cos(att(1)) sin(att(1));
0 -sin(att(1)) cos(att(1))];
C_2=[cos(att(2)) 0 -sin(att(2));
0 1 0;
sin(att(2)) 0 cos(att(2))];
C_3=[cos(att(3)) -sin(att(3)) 0;
sin(att(3)) cos(att(3)) 0;
0 0 1];
Mat=(C_2*C_1*C_3)';
end
1.2算法程序

用到的子函数
function [ MRV ] = MRV( phi )
n=length(phi);
phi_fan=Fan(phi);
phi_2=norm(phi,2);
MRV=eye(n)+sin(phi_2)/phi_2*phi_fan+(1-cos(phi_2))/phi_2^2*phi_fan^2;
end
function [ phi_fan ] = Fan( phi )
% 反对称阵
phi_fan=[0 -phi(3) phi(2);phi(3) 0 -phi(1);-phi(2) phi(1) 0];
end
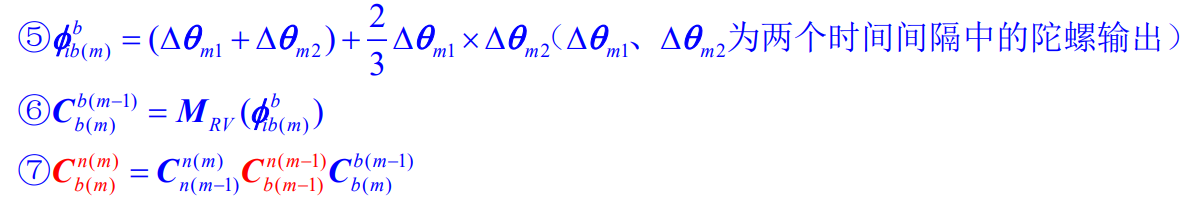
1.3最后将姿态矩阵转化为姿态角
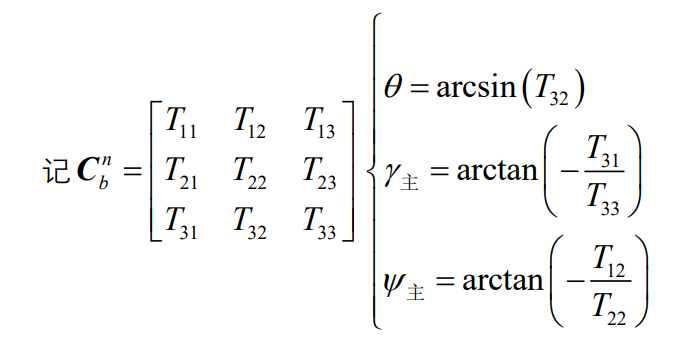
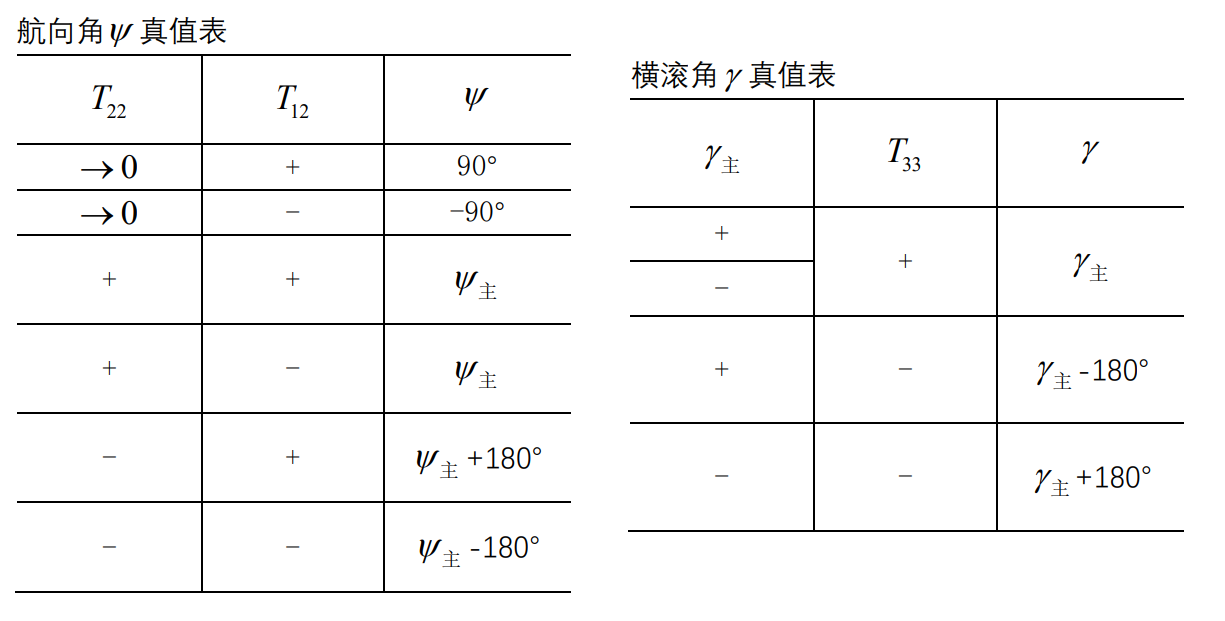
在Matlab中可以直接进行转化,不需要判断,程序如下:
function [ att ] = Mat2Att_sins( Mat )
%姿态矩阵转化为姿态角,转化结果单位为度
att=[asind(Mat(3,2)) rad2deg(atan2(-Mat(3,1),Mat(3,3))) rad2deg(atan2(Mat(1,2),Mat(2,2)))];
end
1.4完整姿态更新程序
%姿态更新
C_bn1=Att2Mat_sins(avp1(1:3));%姿态角转化为姿态矩阵
wien_1=[0 wie*cos(avp1(7)) wie*sin(avp1(7))]';
wenn_1=[-avp1(5)/(R_M_1+avp1(9)) avp1(4)/(R_N_1+avp1(9)) tan(avp1(7))*avp1(4)/(R_N_1+avp1(9))]';
winn_1=wien_1+wenn_1;
C_nn=MRV(Tm*winn_1)';
phi_ibb=(delta_theta1+delta_theta2)+2/3*cross(delta_theta1,delta_theta2);
C_bb=MRV(phi_ibb);
C_bn2=C_nn*C_bn1*C_bb;%姿态更新
avp2(1:3)=Mat2Att_sins(C_bn2);%姿态矩阵转化为姿态角
2.速度更新算法

数据外推程序
function [y10 ] = waitui( y1,y0 )
%数据外推
y10=(3*y1-y0)/2;
end
第一次解算速度更新算法:
%速度更新
deltav_rot=1/2*cross((delta_theta1+delta_theta2),(delta_v1+delta_v2));
deltav_scul=2/3*(cross(delta_theta1,delta_v2)+cross(delta_v1,delta_theta2));
deltav_sfm=(eye(3)-Tm/2*Fan(winn_1))*C_bn1*(delta_v1+delta_v2+deltav_rot+deltav_scul)';
g=g0*(1+5.27094e-3*sin(avp1(7))^2+2.32718e-5*sin(avp1(7))^4)-3.086e-6*avp1(9);
gn=[0 0 -g];
deltav_cor=(gn-cross((2*wien_1+wenn_1),avp1(4:6)))*Tm;
avp2(4:6)=avp1(4:6)+deltav_sfm'+deltav_cor;%速度更新
后续解算使用外推数据更新算法
%外推数据速度更新
wien_0=[0 wie*cos(avp0(7)) wie*sin(avp0(7))]';
wenn_0=[-avp0(5)/(R_M_0+avp0(9)) avp0(4)/(R_N_0+avp0(9)) tan(avp0(7))*avp0(4)/(R_N_0+avp0(9))]';
wien_10=waitui(wien_1,wien_0);
wenn_10=waitui(wenn_1,wenn_0);
winn_10=wien_10+wenn_10;%x_10代表外推数据
deltav_rot=1/2*cross((delta_theta1+delta_theta2),(delta_v1+delta_v2));
deltav_scul=2/3*(cross(delta_theta1,delta_v2)+cross(delta_v1,delta_theta2));
deltav_sfm=(eye(3)-Tm/2*Fan(winn_10))*C_bn1*(delta_v1+delta_v2+deltav_rot+deltav_scul)';
g_1=g0*(1+5.27094e-3*sin(avp1(7))^2+2.32718e-5*sin(avp1(7))^4)-3.086e-6*avp1(9);
g_0=g0*(1+5.27094e-3*sin(avp0(7))^2+2.32718e-5*sin(avp0(7))^4)-3.086e-6*avp0(9);
gn=[0 0 -waitui(g_1,g_0)];
deltav_cor=(gn-cross((2*wien_10+wenn_10),waitui(avp1(4:6),avp0(4:6))))*Tm;
avp2(4:6)=avp1(4:6)+deltav_sfm'+deltav_cor;%速度更新
3.位置更新算法
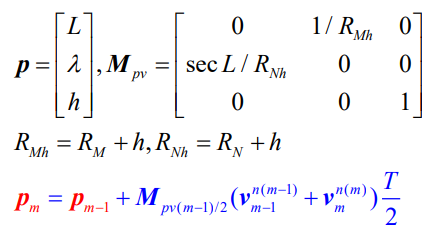
对矩阵可以使用整体外推法,也可以对矩阵中的元素外推,再构造矩阵,程序中使用整体外推法。
第一次解算位置更新程序
%位置更新
Mpv=[0 1/(R_M_1+avp1(9)) 0; sec(avp1(7))/(R_N_1+avp1(9)) 0 0;0 0 1];
avp2(7:9)=avp1(7:9)+(Mpv*(avp1(4:6)+avp2(4:6))'*Tm/2)';%位置更新
后续使用外推解算位置更新程序
%外推数据位置更新
Mpv_1=[0 1/(R_M_1+avp1(9)) 0; sec(avp1(7))/(R_N_1+avp1(9)) 0 0;0 0 1];
Mpv_0=[0 1/(R_M_0+avp0(9)) 0; sec(avp0(7))/(R_N_0+avp0(9)) 0 0;0 0 1];
Mpv=waitui(Mpv_1,Mpv_0);%使用对矩阵Mpv整体外推法
avp2(7:9)=avp1(7:9)+(Mpv*(avp1(4:6)+avp2(4:6))'*Tm/2)';%位置更新
附录(完整程序)
程序清单:
1、主函数
2、主要子函数(2个):第一次解算函数、后续使用外推数据解算函数
3、其他子函数(5个):姿态角转化为姿态矩阵函数、姿态矩阵转化为姿态角函数、等效旋转矢量函数、反对称矩阵函数、数据外推函数
主函数
clc
clear
load imu.mat;%1-3列:陀螺仪xyz轴数据(单位:弧度)、4-6列:加速度计xyz轴数据(单位m/s)、第7列为时间
ins_data=zeros(length(imu)/2+1,10);%俯仰、横滚、航向角、xyz轴速度、纬度、经度、高度、时间,角度单位为度
ins_data(1,:)=[0 0 -10*180/pi 0 0 0 34 106 380 0];%初始值,最后一列为时间
ins_data(2,:)=sins(ins_data(1,:),imu(1:2,:));%第一次解算不使用外推
for k=4:2:length(imu)
%使用二子样算法,每次输入两次的惯性器件采样数据和前两时刻的avp数据
ins_data(k/2+1,:)=sins_waitui(ins_data(k/2,:),ins_data(k/2-1,:),imu(k-1:k,:));
end
第一次解算函数
function [ avp2 ] = sins( avp1,imu )
%imu数据
Tm=2*(imu(2,7)-imu(1,7));
delta_theta1=imu(1,1:3);delta_theta2=imu(2,1:3);
delta_v1=imu(1,4:6);delta_v2=imu(2,4:6);
%参数
Re=6378254;%单位:m
f=1/298.3;
wie=7.292115e-5;%单位:rad/s
g0=9.780325333434361;%单位;m/s^2
e2=2*f-f^2;
R_N_1=Re/sqrt(1-e2*sin(avp1(7)));
R_M_1=R_N_1*(1-e2)/(1-e2*sin(avp1(7))^2);
avp1([1:3 7 8])=deg2rad(avp1([1:3 7 8]));%将所有角度转化为弧度,结算中用到的角度都是弧度单位
%姿态更新
C_bn1=Att2Mat_sins(avp1(1:3));%姿态角转化为姿态矩阵
wien_1=[0 wie*cos(avp1(7)) wie*sin(avp1(7))]';
wenn_1=[-avp1(5)/(R_M_1+avp1(9)) avp1(4)/(R_N_1+avp1(9)) tan(avp1(7))*avp1(4)/(R_N_1+avp1(9))]';
winn_1=wien_1+wenn_1;
C_nn=MRV(Tm*winn_1)';
phi_ibb=(delta_theta1+delta_theta2)+2/3*cross(delta_theta1,delta_theta2);
C_bb=MRV(phi_ibb);
C_bn2=C_nn*C_bn1*C_bb;%姿态更新
avp2(1:3)=Mat2Att_sins(C_bn2);%姿态矩阵转化为姿态角
%速度更新
deltav_rot=1/2*cross((delta_theta1+delta_theta2),(delta_v1+delta_v2));
deltav_scul=2/3*(cross(delta_theta1,delta_v2)+cross(delta_v1,delta_theta2));
deltav_sfm=(eye(3)-Tm/2*Fan(winn_1))*C_bn1*(delta_v1+delta_v2+deltav_rot+deltav_scul)';
g=g0*(1+5.27094e-3*sin(avp1(7))^2+2.32718e-5*sin(avp1(7))^4)-3.086e-6*avp1(9);
gn=[0 0 -g];
deltav_cor=(gn-cross((2*wien_1+wenn_1),avp1(4:6)))*Tm;
avp2(4:6)=avp1(4:6)+deltav_sfm'+deltav_cor;%速度更新
%位置更新
Mpv=[0 1/(R_M_1+avp1(9)) 0; sec(avp1(7))/(R_N_1+avp1(9)) 0 0;0 0 1];
avp2(7:9)=avp1(7:9)+(Mpv*(avp1(4:6)+avp2(4:6))'*Tm/2)';%位置更新
avp2(7:8)=rad2deg(avp2(7:8));%将角度坐标转化为弧度
avp2(10)=imu(2,7);%时间
end
后续使用外推数据解算函数
function [ avp2 ] = sins_waitui( avp1,avp0,imu )
%imu数据
Tm=2*(imu(2,7)-imu(1,7));
delta_theta1=imu(1,1:3);delta_theta2=imu(2,1:3);
delta_v1=imu(1,4:6);delta_v2=imu(2,4:6);
%参数
Re=6378254;%单位:m
f=1/298.3;
wie=7.292115e-5;%单位:rad/s
g0=9.780325333434361;%单位;m/s^2
e2=2*f-f^2;
R_N_0=Re/sqrt(1-e2*sin(avp0(7)));
R_M_0=R_N_0*(1-e2)/(1-e2*sin(avp0(7))^2);
R_N_1=Re/sqrt(1-e2*sin(avp1(7)));
R_M_1=R_N_1*(1-e2)/(1-e2*sin(avp1(7))^2);
avp1([1:3 7 8])=deg2rad(avp1([1:3 7 8]));
avp0([1:3 7 8])=deg2rad(avp0([1:3 7 8]));
%姿态更新
C_bn1=Att2Mat_sins(avp1(1:3));%姿态角转化为姿态矩阵
wien_1=[0 wie*cos(avp1(7)) wie*sin(avp1(7))]';
wenn_1=[-avp1(5)/(R_M_1+avp1(9)) avp1(4)/(R_N_1+avp1(9)) tan(avp1(7))*avp1(4)/(R_N_1+avp1(9))]';
winn_1=wien_1+wenn_1;
C_nn=MRV(Tm*winn_1)';
phi_ibb=(delta_theta1+delta_theta2)+2/3*cross(delta_theta1,delta_theta2);
C_bb=MRV(phi_ibb);
C_bn2=C_nn*C_bn1*C_bb;%姿态更新
avp2(1:3)=Mat2Att_sins(C_bn2);%姿态矩阵转化为姿态角
%速度更新
wien_0=[0 wie*cos(avp0(7)) wie*sin(avp0(7))]';
wenn_0=[-avp0(5)/(R_M_0+avp0(9)) avp0(4)/(R_N_0+avp0(9)) tan(avp0(7))*avp0(4)/(R_N_0+avp0(9))]';
wien_10=waitui(wien_1,wien_0);
wenn_10=waitui(wenn_1,wenn_0);
winn_10=wien_10+wenn_10;%x_10代表外推数据
deltav_rot=1/2*cross((delta_theta1+delta_theta2),(delta_v1+delta_v2));
deltav_scul=2/3*(cross(delta_theta1,delta_v2)+cross(delta_v1,delta_theta2));
deltav_sfm=(eye(3)-Tm/2*Fan(winn_10))*C_bn1*(delta_v1+delta_v2+deltav_rot+deltav_scul)';
g_1=g0*(1+5.27094e-3*sin(avp1(7))^2+2.32718e-5*sin(avp1(7))^4)-3.086e-6*avp1(9);
g_0=g0*(1+5.27094e-3*sin(avp0(7))^2+2.32718e-5*sin(avp0(7))^4)-3.086e-6*avp0(9);
gn=[0 0 -waitui(g_1,g_0)];
deltav_cor=(gn-cross((2*wien_10+wenn_10),waitui(avp1(4:6),avp0(4:6))))*Tm;
avp2(4:6)=avp1(4:6)+deltav_sfm'+deltav_cor;%速度更新
%位置更新
Mpv_1=[0 1/(R_M_1+avp1(9)) 0; sec(avp1(7))/(R_N_1+avp1(9)) 0 0;0 0 1];
Mpv_0=[0 1/(R_M_0+avp0(9)) 0; sec(avp0(7))/(R_N_0+avp0(9)) 0 0;0 0 1];
Mpv=waitui(Mpv_1,Mpv_0);%使用对矩阵Mpv整体外推法
avp2(7:9)=avp1(7:9)+(Mpv*(avp1(4:6)+avp2(4:6))'*Tm/2)';%位置更新
avp2(7:8)=rad2deg(avp2(7:8));%将角度坐标转化为弧度
avp2(10)=imu(2,7);%时间
end
姿态角转化为姿态矩阵函数
function [ Mat ] = Att2Mat_sins( att )
%姿态角转化为姿态矩阵
C_1=[ 1 0 0;
0 cos(att(1)) sin(att(1));
0 -sin(att(1)) cos(att(1))];
C_2=[cos(att(2)) 0 -sin(att(2));
0 1 0;
sin(att(2)) 0 cos(att(2))];
C_3=[cos(att(3)) -sin(att(3)) 0;
sin(att(3)) cos(att(3)) 0;
0 0 1];
Mat=(C_2*C_1*C_3)';
end
姿态矩阵转化为姿态角函数
function [ att ] = Mat2Att_sins( Mat )
%姿态矩阵转化为姿态角,转化结果单位为度
att=[asind(Mat(3,2)) rad2deg(atan2(-Mat(3,1),Mat(3,3))) rad2deg(atan2(Mat(1,2),Mat(2,2)))];
end
等效旋转矢量函数
function [ MRV ] = MRV( phi )
n=length(phi);
phi_fan=Fan(phi);
phi_2=norm(phi,2);
MRV=eye(n)+sin(phi_2)/phi_2*phi_fan+(1-cos(phi_2))/phi_2^2*phi_fan^2;
end
反对称矩阵函数
function [ phi_fan ] = Fan( phi )
% 反对称阵
phi_fan=[0 -phi(3) phi(2);phi(3) 0 -phi(1);-phi(2) phi(1) 0];
end
数据外推函数
function [y10 ] = waitui( y1,y0 )
%数据外推
y10=(3*y1-y0)/2;
end
























 1286
1286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








