LBP特征

最新推荐文章于 2019-05-26 13:44:32 发布

羊肉串串魅力无穷

最新推荐文章于 2019-05-26 13:44:32 发布

阅读量5.5w

点赞数 73

分类专栏：图像 - 特征提取

本文链接：https://blog.csdn.net/lk3030/article/details/84034963

版权

图像 - 特征提取专栏收录该内容

4 篇文章

订阅专栏

LBP是Local Binary Pattern（局部二值模式）的缩写，具有灰度不变性和旋转不变性等显著优点。由于该特征的简单易算性，虽然其总体效果不如Haar特征，但速度则快于Haar，所以也得到了广泛的使用。

文章目录

LBP特征的描述

原始的LBP算子定义为在 $3 * 3$ 的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于等于中心像素值，则该像素点的位置被标记为1，否则为0。这样， $3 * 3$ 邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。需要注意的是，LBP值是按照顺时针方向组成的二进制数。

LBP特征的圆形化改进

基本的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala等对 LBP 算子进行了改进，将 3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子，称为Extended LBP，也叫Circular LBP。

比如下图定了一个5x5的邻域：

上图内有八个黑色的采样点，每个采样点的值可以通过下式计算：

$x_p = x_c+R\cos( \frac{2\pi p}{P} )$

$y_p = y_c-R\sin( \frac{2\pi p}{P} )$

其中 $x_c，y_c)$ 为邻域中心点， $x_p，y_p)$ 为某个采样点。通过上式可以计算任意个采样点的坐标，但是计算得到的坐标未必完全是整数，所以可以通过双线性插值来得到该采样点的像素值：

$f(x,y)\approx \begin{bmatrix} 1-x & x \\ \end{bmatrix} \begin{bmatrix} f(0,0) & f(0,1)\\ f(1,0) & f(1,1) \end{bmatrix}\begin{bmatrix} 1-y\\ y \end{bmatrix}$

几种不同半径不同采样点的LBP算子：

LBP旋转不变模式

下图中的8种 LBP 模式，对应的旋转不变的 LBP模式都是00001111，即 LBP值为 15：

Uniform Pattern LBP等价模式

一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生 $2^P$ 种模式。为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”来对LBP算子的模式种类进行降维。

Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类，除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111(共四次跳变)。。

通过这样的改进，模式数量由原来的 $2^P$ 种减少为 $P (P - 1) + 2$ 种，其中 $P$ 表示邻域集内的采样点数。对于 $3 \times 3$ 邻域内8个采样点来说，二进制模式由原始的256种减少为58种，他们对应的值按照从小到大分别编码为1-58，即它们在LBP特征图像中的灰度值为1-58，而除了等价模式类之外的混合模式类被编码为0，即它们在LBP特征中的灰度值为0，因此等价模式LBP特征图像整体偏暗。这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。

LBP特征用于检测的原理

上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”，那么，对一幅图像（记录的是每个像素点的灰度值）提取其原始的LBP算子之后，得到的原始LBP特征依然是“一幅图片”（记录的是每个像素点的LBP值）。

LBP的应用中，如纹理分类、人脸分析等，一般都不将LBP图谱作为特征向量用于分类识别，而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。

例如：一幅 $100 * 100$ 像素大小的图片，划分为 $10 * 10 = 100$ 个子区域，也就有了 $10 * 10$ 个统计直方图，利用这 $10 * 10$ 个统计直方图，以及各种相似性度量函数，就可以判断两幅图像之间的相似性了。

MB-LBP特征

MB-LBP特征，全称为Multiscale Block LBP，在Traincascade级联目标训练检测中的LBP特征使用的就是MB-LBP。

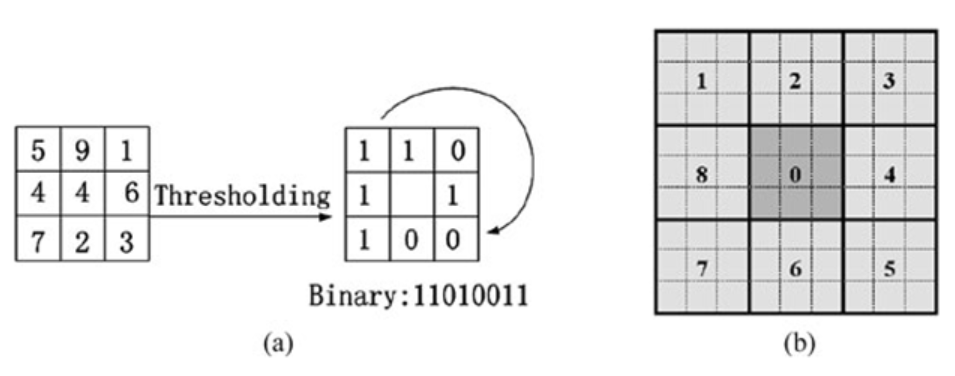
将图像分成一个个小块（Block），每个小块再分为一个个的小区域（类似于HOG中的cell），小区域内的灰度平均值作为当前小区域的灰度值，与周围小区域灰度进行比较形成LBP特征，生成的特征称为MB-LBP。Block大小为 $3 * 3$ 且小区域的大小为1时，就是原始的LBP特征，上图的Block大小为 $9 * 9$ ，小区域的大小为 $3 * 3$ 。

作者对得到LBP特征又进行了均值模式编码，通过对得到的特征图求直方图，得到了LBP特征值0-255之间(0-255即直方图中的bin)的特征数量，通过对bin中的数值进行排序，通过权衡，将排序在前63位的特征值看作是等价模式类，其他的为混合模式类，总共64类，作者在论文中称之为SEMB-LBP(Statistically Effective MB-LBP )。类似于等价模式LBP，等价模式的LBP的等价模式类为58种，混合模式类1种，共59种。二者除了等价模式类的数量不同之外，主要区别在于：对等价模式类的定义不同，等价模式LBP是根据0-1的跳变次数定义的，而SEMB-LBP是通过对直方图排序得到的。

总结：MB-LBP有点类似于先将图像进行平滑处理，然后再求LBP特征。而SEMB-LBP是在MB-LBP进行编码后的图像。类似于等价模式LBP，先求LBP特征，再用等价模式进行编码。当Scale=3时，MB-LBP和SEMB-LBP就是LBP和等价模式LBP。

LBPH，图像的LBP特征向量

LBPH，Local Binary Patterns Histograms，即LBP特征的统计直方图，LBPH将LBP特征与图像的空间信息结合在一起。将LBP特征图像分成m个局部块，并提取每个局部块的直方图，然后将这些直方图依次连接在一起形成LBP特征的统计直方图，即LBPH。

一幅图像具体的计算LBPH的过程（以Opencv中的人脸识别为例）：

计算图像的LBP特征图像。
将LBP特征图像进行分块，Opencv中默认将LBP特征图像分成8行8列64块区域
计算每块区域特征图像的直方图cell_LBPH，将直方图进行归一化，直方图大小为 $1 * n u m P a t t e r n s$
将每块区域的直方图按空间顺序依次排列成一行，形成LBP特征向量，大小为 $1 * (n u m P a t t e r n s * 64)$
用机器学习的方法对LBP特征向量进行训练，用来检测和识别目标

举例说明LBPH的维度：
采样点为8个，如果用的是原始的LBP或Extended LBP特征，其LBP特征值的模式为256种，则一幅图像的LBP特征向量维度为： $64 * 256 = 16384$ 维，而如果使用的UniformPatternLBP特征，其LBP值的模式为59种，其特征向量维度为： $64 * 59 = 3776$ 维，可以看出，使用等价模式特征，其特征向量的维度大大减少，这意味着使用机器学习方法进行学习的时间将大大减少，而性能上没有受到很大影响。Opencv的人脸识别使用的是Extended LBP。

LBP算子的优缺点

优点:

一定程度上消除了光照变化的问题
具有旋转不变性
纹理特征维度低，计算速度快

缺点:

当光照变化不均匀时,各像素间的大小关系被破坏,对应的LBP算子也就发生了变化。
通过引入旋转不变的定义,使LBP算子更具鲁棒性。但这也使得LBP算子丢失了方向信息。

计算原始LBP特征值

import cv2
import numpy as np

def origin_LBP(img):
    dst = np.zeros(img.shape,dtype=img.dtype)
    h,w=img.shape
    for i in range(1,h-1):
        for j in range(1,w-1):
            center = img[i][j]
            code = 0
             
            code |= (img[i-1][j-1] >= center) << (np.uint8)(7)  
            code |= (img[i-1][j  ] >= center) << (np.uint8)(6)  
            code |= (img[i-1][j+1] >= center) << (np.uint8)(5)  
            code |= (img[i  ][j+1] >= center) << (np.uint8)(4)  
            code |= (img[i+1][j+1] >= center) << (np.uint8)(3)  
            code |= (img[i+1][j  ] >= center) << (np.uint8)(2)  
            code |= (img[i+1][j-1] >= center) << (np.uint8)(1)  
            code |= (img[i  ][j-1] >= center) << (np.uint8)(0)  
  
            dst[i-1][j-1]= code
    return dst

gray = cv2.imread('C:/Users/Ivy/Desktop/a.jpg', cv2.IMREAD_GRAYSCALE)
cv2.imshow('img', gray)
org_lbp = origin_LBP(gray)
cv2.imshow('org_lbp', org_lbp)
cv2.waitKey(0)

计算圆形LBP特征值

半径越小，图像纹理越精细，邻域数目越小，图像亮度越低。

原始图 / 原始LBP / 圆形R1P8 / 圆形R3P8 / 圆形R3P6

import cv2
import numpy as np

def circular_LBP(img, radius=3, neighbors=8):
    h,w=img.shape
    dst = np.zeros((h-2*radius, w-2*radius),dtype=img.dtype)
    for k in range(neighbors):
        # 计算采样点对于中心点坐标的偏移量rx，ry
        rx = radius * np.cos(2.0 * np.pi * k / neighbors)
        ry = -(radius * np.sin(2.0 * np.pi * k / neighbors))
        # 为双线性插值做准备
        # 对采样点偏移量分别进行上下取整
        x1 = int(np.floor(rx))
        x2 = int(np.ceil(rx))
        y1 = int(np.floor(ry))
        y2 = int(np.ceil(ry))
        # 将坐标偏移量映射到0-1之间
        tx = rx - x1
        ty = ry - y1
        # 根据0-1之间的x，y的权重计算公式计算权重，权重与坐标具体位置无关，与坐标间的差值有关
        w1 = (1-tx) * (1-ty)
        w2 =    tx  * (1-ty)
        w3 = (1-tx) *    ty
        w4 =    tx  *    ty
        for i in range(radius,h-radius):
            for j in range(radius,w-radius):
                # 获得中心像素点的灰度值
                center = img[i,j]
                # 根据双线性插值公式计算第k个采样点的灰度值
                neighbor = img[i+y1,j+x1] * w1 + img[i+y2,j+x1] *w2 + img[i+y1,j+x2] *  w3 +img[i+y2,j+x2] *w4
                # LBP特征图像的每个邻居的LBP值累加，累加通过与操作完成，对应的LBP值通过移位取得
                dst[i-radius,j-radius] |= (neighbor>center)  <<  (np.uint8)(neighbors-k-1)
    return dst

gray = cv2.imread('C:/Users/Ivy/Desktop/a.jpg', cv2.IMREAD_GRAYSCALE)
cv2.imshow('img', gray)
circul_1_8 = circular_LBP(gray,1,8)
circul_3_8 = circular_LBP(gray,3,8)
circul_3_6 = circular_LBP(gray,3,6)
cv2.imshow('18', circul_1_8)
cv2.imshow('38', circul_3_8)
cv2.imshow('36', circul_3_6)
cv2.waitKey(0)

计算旋转不变圆形LBP特征值

原始图 / 原始LBP / 圆形R3P8 / 旋转不变R3P8

import cv2
import numpy as np

def rotation_invariant_LBP(img, radius=3, neighbors=8):
    h,w=img.shape
    dst = np.zeros((h-2*radius, w-2*radius),dtype=img.dtype)
    for k in range(neighbors):
        # 计算采样点对于中心点坐标的偏移量rx，ry
        rx = radius * np.cos(2.0 * np.pi * k / neighbors)
        ry = -(radius * np.sin(2.0 * np.pi * k / neighbors))
        # 为双线性插值做准备
        # 对采样点偏移量分别进行上下取整
        x1 = int(np.floor(rx))
        x2 = int(np.ceil(rx))
        y1 = int(np.floor(ry))
        y2 = int(np.ceil(ry))
        # 将坐标偏移量映射到0-1之间
        tx = rx - x1
        ty = ry - y1
        # 根据0-1之间的x，y的权重计算公式计算权重，权重与坐标具体位置无关，与坐标间的差值有关
        w1 = (1-tx) * (1-ty)
        w2 =    tx  * (1-ty)
        w3 = (1-tx) *    ty
        w4 =    tx  *    ty
        for i in range(radius,h-radius):
            for j in range(radius,w-radius):
                # 获得中心像素点的灰度值
                center = img[i,j]
                # 根据双线性插值公式计算第k个采样点的灰度值
                neighbor = img[i+y1,j+x1] * w1 + img[i+y2,j+x1] *w2 + img[i+y1,j+x2] *  w3 +img[i+y2,j+x2] *w4
                # LBP特征图像的每个邻居的LBP值累加，累加通过与操作完成，对应的LBP值通过移位取得
                dst[i-radius,j-radius] |= (neighbor>center)  <<  (np.uint8)(neighbors-k-1)
    # 进行旋转不变处理
    for i in range(dst.shape[0]):
        for j in range(dst.shape[1]):
            currentValue = dst[i,j]
            minValue = currentValue;
            for k in range(1, neighbors):
                # 循环左移
                temp = (np.uint8)(currentValue>>(neighbors-k)) |  (np.uint8)(currentValue<<k)
                if temp < minValue:
                    minValue = temp
                
            dst[i,j] = minValue
    
    return dst       

gray = cv2.imread('C:/Users/Ivy/Desktop/a.jpg', cv2.IMREAD_GRAYSCALE)
cv2.imshow('img', gray)
rotation_invariant = rotation_invariant_LBP(gray,3,8)
cv2.imshow('ri', rotation_invariant)
cv2.waitKey(0)

计算Uniform Pattern LBP特征值

原始图 / 圆形R3P8 / 旋转不变R3P8 / UPLBP,R3P8 / UPLBP,R3P8增强亮度显示

import cv2
import numpy as np

def uniform_pattern_LBP(img,radius=3, neighbors=8):
    h,w=img.shape
    dst = np.zeros((h-2*radius, w-2*radius),dtype=img.dtype)
    # LBP特征值对应图像灰度编码表，直接默认采样点为8位
    temp = 1
    table =np.zeros((256),dtype=img.dtype)
    for i in range(256):
        if getHopTimes(i)<3:
            table[i] = temp
            temp+=1
    # 是否进行UniformPattern编码的标志
    flag = False
    # 计算LBP特征图
    for k in range(neighbors):
        if k==neighbors-1:
            flag = True
      
        # 计算采样点对于中心点坐标的偏移量rx，ry
        rx = radius * np.cos(2.0 * np.pi * k / neighbors)
        ry = -(radius * np.sin(2.0 * np.pi * k / neighbors))
        # 为双线性插值做准备
        # 对采样点偏移量分别进行上下取整
        x1 = int(np.floor(rx))
        x2 = int(np.ceil(rx))
        y1 = int(np.floor(ry))
        y2 = int(np.ceil(ry))
        # 将坐标偏移量映射到0-1之间
        tx = rx - x1
        ty = ry - y1
        # 根据0-1之间的x，y的权重计算公式计算权重，权重与坐标具体位置无关，与坐标间的差值有关
        w1 = (1-tx) * (1-ty)
        w2 =    tx  * (1-ty)
        w3 = (1-tx) *    ty
        w4 =    tx  *    ty
        # 循环处理每个像素
        for i in range(radius,h-radius):
            for j in range(radius,w-radius):
                # 获得中心像素点的灰度值
                center = img[i,j]
                # 根据双线性插值公式计算第k个采样点的灰度值
                neighbor = img[i+y1,j+x1] * w1 + img[i+y2,j+x1] *w2 + img[i+y1,j+x2] *  w3 +img[i+y2,j+x2] *w4
                # LBP特征图像的每个邻居的LBP值累加，累加通过与操作完成，对应的LBP值通过移位取得
                dst[i-radius,j-radius] |= (neighbor>center)  <<  (np.uint8)(neighbors-k-1)
                # 进行LBP特征的UniformPattern编码
                if flag:
                    dst[i-radius,j-radius] = table[dst[i-radius,j-radius]]
    return dst
             
def getHopTimes(data):
    '''
    计算跳变次数
    '''
    count = 0;
    binaryCode = "{0:0>8b}".format(data)
     
    for i in range(1,len(binaryCode)):
        if binaryCode[i] != binaryCode[(i-1)]:
            count+=1
    return count

gray = cv2.imread('C:/Users/Ivy/Desktop/a.jpg', cv2.IMREAD_GRAYSCALE)
cv2.imshow('img', gray)
uniform_pattern = uniform_pattern_LBP(gray,3,8)
cv2.imshow('up', uniform_pattern)
cv2.waitKey(0)

计算MB-LBP特征值

原始图 / 原始LBP / MBLBP 3 / MBLBP 9 / MBLBP 15

import cv2
import numpy as np

def multi_scale_block_LBP(img,scale):
    h,w= img.shape
    
    # 定义并计算积分图像
    cellSize = int(scale / 3)
    offset = int(cellSize / 2)
    cellImage = np.zeros((h-2*offset, w-2*offset),dtype=img.dtype)
      
    for i in range(offset,h-offset):
        for j in range(offset,w-offset):
            temp = 0;
            for m in range(-offset,offset+1):
                for n in range(-offset,offset+1):  
                    temp += img[i+n,j+m]
                
            temp /= (cellSize*cellSize);
            cellImage[i-int(cellSize/2),j-int(cellSize/2)] = np.uint8(temp)
             
    dst = origin_LBP(cellImage)
    return dst

gray = cv2.imread('C:/Users/Ivy/Desktop/a.jpg', cv2.IMREAD_GRAYSCALE)
cv2.imshow('img', gray)
mb_3 = multi_scale_block_LBP(gray,3)  
mb_9 = multi_scale_block_LBP(gray,9)  
mb_15 = multi_scale_block_LBP(gray,15)  
cv2.imshow('mb_3', mb_3)
cv2.imshow('mb_9', mb_9)
cv2.imshow('mb_15', mb_15)
cv2.waitKey(0)

计算图像的LBPH特征向量

def getLBPH(img_lbp,numPatterns,grid_x,grid_y,normed):
    '''
    计算LBP特征图像的直方图LBPH
    '''
    h,w=img_lbp.shape
    width = int(w / grid_x)
    height = int(h / grid_y)
    # 定义LBPH的行和列，grid_x*grid_y表示将图像分割的块数，numPatterns表示LBP值的模式种类
    result = np.zeros((grid_x * grid_y,numPatterns),dtype=float)
    resultRowIndex = 0
    # 对图像进行分割，分割成grid_x*grid_y块，grid_x，grid_y默认为8
    for i in range(grid_x):
        for j in range(grid_y):
            # 图像分块
            src_cell = img_lbp[i*height:(i+1)*height,j*width:(j+1)*width]
            # 计算直方图
            hist_cell = getLocalRegionLBPH(src_cell,0,(numPatterns-1),True)
            #将直方图放到result中
            result[resultRowIndex]=hist_cell
            resultRowIndex+=1
    return np.reshape(result,(-1))

def getLocalRegionLBPH(src,minValue,maxValue,normed):
    '''
    计算一个LBP特征图像块的直方图
    '''
    data = np.reshape(src,(-1))
    # 计算得到直方图bin的数目，直方图数组的大小
    bins = maxValue - minValue + 1;
    # 定义直方图每一维的bin的变化范围
    ranges = (float(minValue),float(maxValue + 1))
    hist, bin_edges = np.histogram(src, bins=bins, range=ranges, normed=normed)
    return hist

uniform_pattern = uniform_pattern_LBP(gray,3,8)
lbph = getLBPH(uniform_pattern,59,8,8,True)