卷积神经网络基础:
首先看一下全连接网络,即神经元和相邻层上的每个神经元都连接:
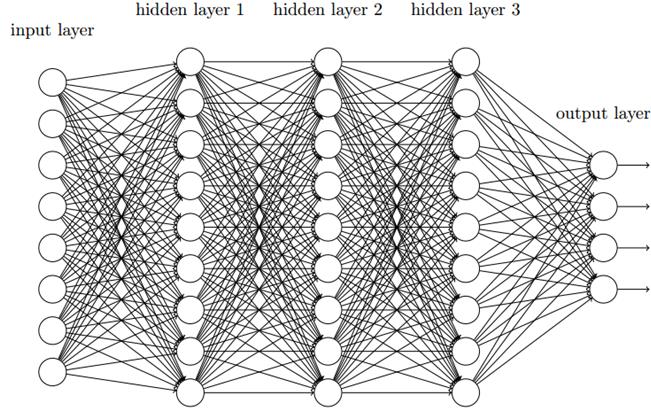
如果我们把图像中的像素点顺序排列作为输入层神经元的值,对于28x28像素的图像,输入神经元有28x28=784个。但是用这种全连接的网络去做图像分类是很奇怪的,因为它没有考虑图像的空间结构(局部特征),它相同看待那些相距很近和很远的像素,这是不好的。
卷积神经网络三个重要概念:
- 局部感受野(local receptive fields)
- 共享权重(shared weights)
- 池化(pooling)
(1)局部感受野:在全连接的网络中,输入被描绘成纵向排列的神经元,但是在卷积网络中我们把它看成28x28的方形:
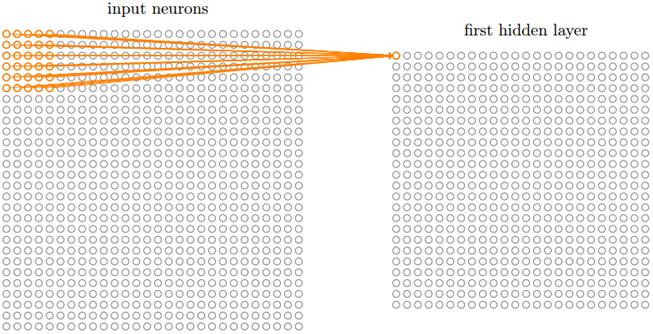
输入神经元的一小片区域会被连接到下一层隐层,这个区域被称为局部感受野,然后在输入图像中移动局部感受野,每移动一次,对应一个隐层的神经元,如此重复构成隐层所有神经元。如果局部感受野是5x5的,一次移动一格,输入图像是28x28的,那么隐层有24x24个神经元。
(2)共享权重和偏置:每个隐层的神经元都有一个偏置和连接到它的局部感受野的5x5的权重,并且对这一层的所有神经元使用相同的权重和偏置。也就是说,对于隐藏层的第j行第k列的神经元,它的输出为:
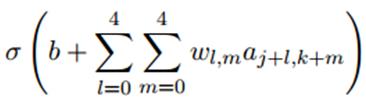
其中σ是激活函数,b是共享偏置,Wl,m是共享权重的5x5数组,用ax,y表示输入层的第x行第y列的神经元的输出值,即隐层的第j行第k列的神经元的若干个输入。
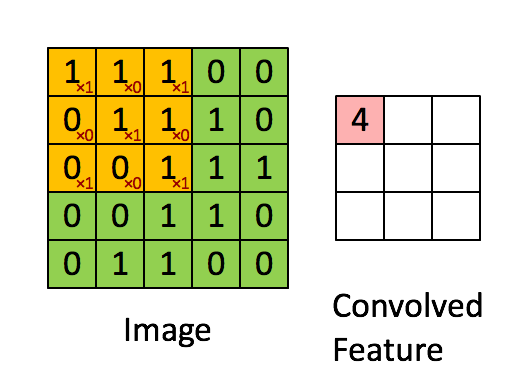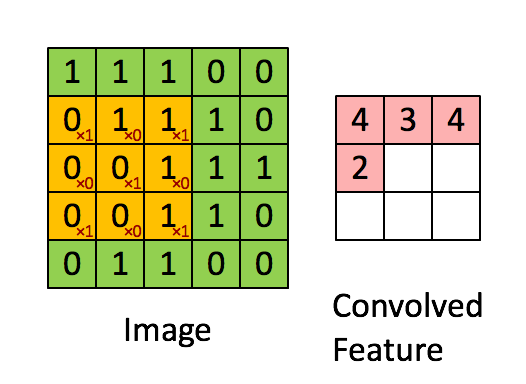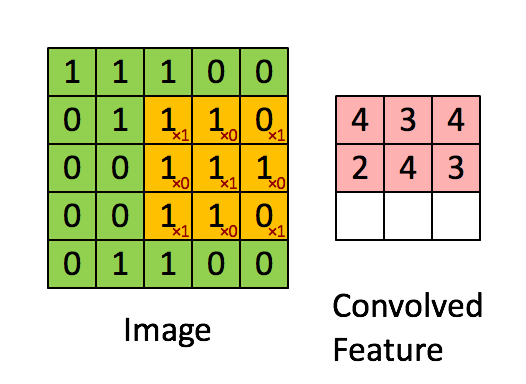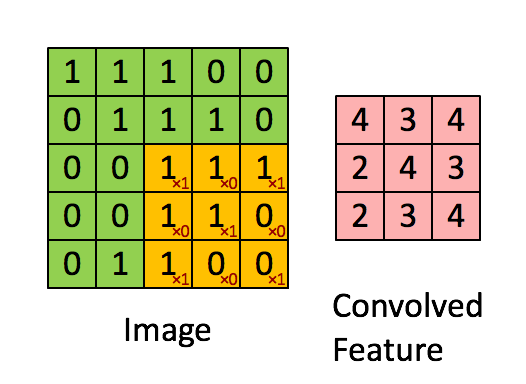
共享,意味着这一个隐层的所有神经元检测完全相同的特征,在输入图像的不同位置。这说明卷积网络可以很好地适应图片的平移不变性。共享权重和偏置被称为卷积核或者滤波器。我们再看一下卷积的过程:
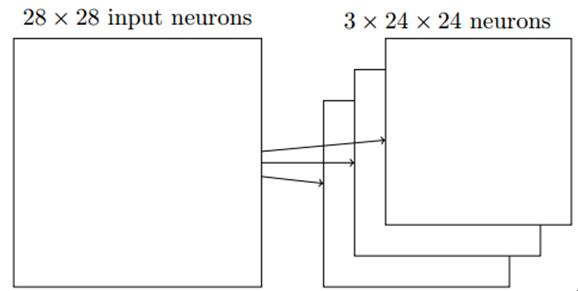
图像分类中我们会卷积多次(卷积核不同),也称为特征映射,下图卷积了3次,识别了3种特征:
共享权重和偏置的一个很大的优点是,大大减少了网络的参数数量。一次卷积我们需要5x5=25个共享权重,加上一个共享偏置共26个参数。如果我们卷积了20次,那么共有20x26=520个参数。以全连接对比,输入神经元有28x28=784个,隐层神经元设为30个,共有784x30个权重,加上30个偏置,共有23550个参数。卷积层的平移不变性会减少参数数量并加快训练,有助于建立深度网络。
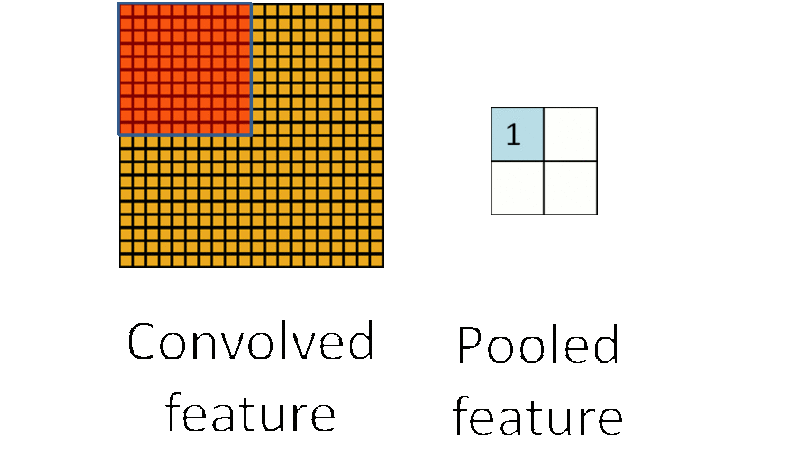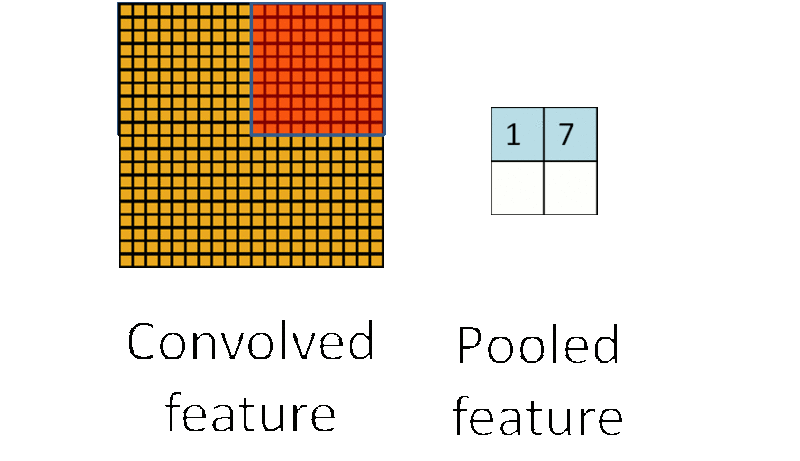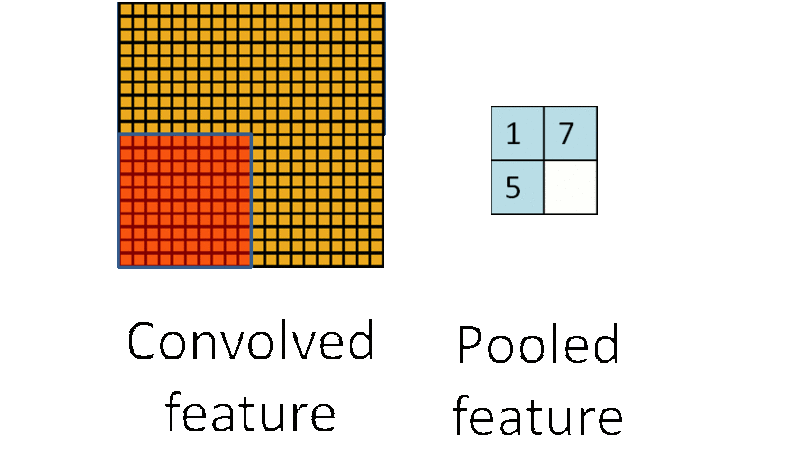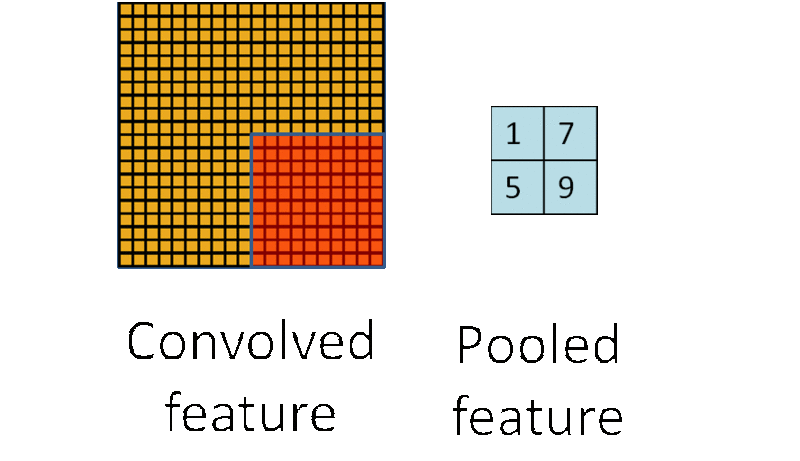
(3)池化:池化层一般在卷积层之后使用,主要是简化从卷积层输出的信息。池化层的每个单元概括了前一层的一个小区域,常见的方法有最大池化,它取前一层那个小区域里的最大值作为对应池化层的值。
为什么要池化呢?在通过卷积获得了特征之后,下一步我们要利用这些特征去做分类,如果直接用这些特征去训练分类器,维度还是太高,计算量太大而且容易过拟合,而通过池化大大减少特征的维度,减少过拟合的出现。再者,我们选择图像中的连续范围作为池化区域,这就意味着即使图像经历了一个小的平移之后,依然会产生相同的 (池化的) 特征,做到了图片的平移不变性。这里也可以看到卷积池化共享权重都有类似的作用。
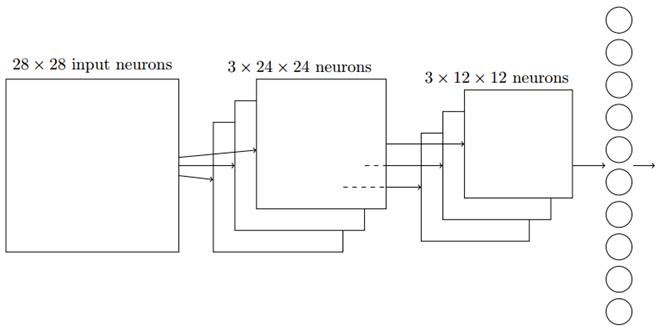
最后要知道,卷积层往往不止一个特征映射,多层卷积的目的是一层卷积学到的特征往往是局部的,层数越高,学到的特征就越全局化。所以我们也将最大池化分别应用于每一个特征映射,如下图,最后是一个输出层,和池化层全连接,一个神经元代表一个类别:
需要注意的是,以上我们举的例子都是单通道的图像,实际上我们的输入图像一般是三通道的,也就是说是一个三维的张量,而对应的卷积核也是三维的,卷积核的“厚度”和输入图像的“厚度”是相同的,三通道就意味着“厚度”为3,所以这个卷积核也是三层。接下来计算第一个通道和卷积核对应第一层的卷积,同样的,计算第二、三个通道和卷积核对应第二、三层的卷积,卷积就是矩阵对应元素相乘之后再相加。最后这三个结果相加,在加上偏置,作为输出。如下图:

如果再多一个卷积核,就再重复一次上边的运算,最后的输出加一层,“厚度”变为2。
卷积神经网络的反向传播:
首先回顾一下一般的前馈神经网络的反向传播:

详细内容可参看:神经网络基础和反向传播推导
1,CNN的前向传播
a)对于卷积层,卷积核与输入矩阵对应位置求积再求和,作为输出矩阵对应位置的值。如果输入矩阵inputX为M*N大小,卷积核为a*b大小,那么输出Y为(M-a+1)*(N-b+1)大小。
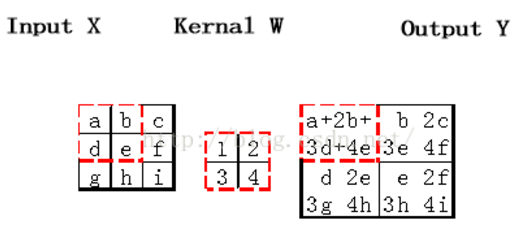
b)对于池化层,按照池化标准把输入张量缩小。
c)对于全连接层,按照普通网络的前向传播计算。
2,CNN反向传播的不同之处:
首先要注意的是,一般神经网络中每一层输入输出a,z都只是一个向量,而CNN中的a,z是一个三维张量,即由若干个输入的子矩阵组成。其次:
- 池化层没有激活函数。这个问题倒比较好解决,我们可以令池化层的激活函数为σ(z)=z,即激活后就是自己本身。这样池化层激活函数的导数为1。
- 池化层在前向传播的时候,对输入进行了压缩,那么我们向前反向推导上一层的误差时,需要做upsample处理。
- 卷积层是通过张量卷积,或者说若干个矩阵卷积求和而得到当前层的输出,这和一般的网络直接进行矩阵乘法得到当前层的输出不同。这样在卷积层反向传播的时候,上一层误差的递推计算方法肯定有所不同。
- 对于卷积层,由于W使用的运算是卷积,那么由该层误差推导出该层的所有卷积核的W,b的方式也不同。
由于卷积层可以有多个卷积核,各个卷积核的处理方法是完全相同且独立的,为了简化算法公式的复杂度,我们下面提到卷积核都是卷积层中若干卷积核中的一个。接下来看具体的CNN反向传播步骤。
3,已知池化层的误差,反向推导上一隐藏层的误差
在前向传播时,池化层我们会用MAX或者Average对输入进行池化,池化的区域大小已知。现在我们反过来,要从缩小后区域的误差,还原前一层较大区域的误差。这个过程叫做upsample。假设我们的池化区域大小是2x2。第l层误差的第k个子矩阵
δlk
为:
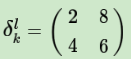
如果池化区域表示为a*a大小,那么我们把上述矩阵上下左右各扩展a-1行和列进行还原:
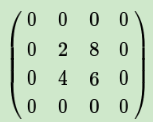
如果是MAX,假设我们之前在前向传播时记录的最大值位置分别是左上,右下,右上,左下,则转换后的矩阵为:
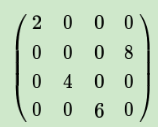
如果是Average,则进行平均,转换后的矩阵为:

上边这个矩阵就是误差矩阵经过upsample之后的矩阵,那么,由后一层误差推导出前一层误差的公式为:
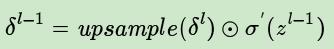
上式和普通网络的反向推导误差很类似:
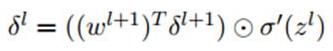
可以看到,只有第一项不同。
4,已知卷积层的误差,反向推导上一隐藏层的误差
公式如下:
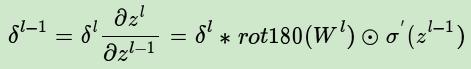
我们再看一次普通网络的反向推导误差的公式:
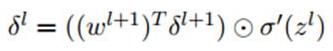
可以看到区别在于,下一层的权重w的转置操作,变成了旋转180度的操作,也就是上下翻转一次,左右再翻转一次,这其实就是“卷积”一词的意义(我们可简单理解为数学上的trick),可参考下图,Q是下一层的误差,周围补0方便计算,W是180度翻转后的卷积核,P是W和Q做卷积的结果:
5,已知卷积层的误差,推导该层的W,b的梯度
经过以上各步骤,我们已经算出每一层的误差了,那么:
a)对于全连接层,可以按照普通网络的反向传播算法求该层W,b的梯度。
b)对于池化层,它并没有W,b,也不用求W,b的梯度。
c)只有卷积层的W,b需要求出,先看w:
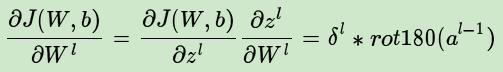
再对比一下普通网络的求w梯度的公式,发现区别在于,对前一层的输出做翻转180度的操作:
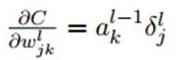
而对于b,则稍微有些特殊,因为在CNN中,误差δ是三维张量,而b只是一个向量,不能像普通网络中那样直接和误差δ相等。通常的做法是将误差δ的各个子矩阵的项分别求和,得到一个误差向量,即为b的梯度:
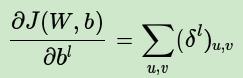
本文内容来自:
1,Michael Nielsen的《Neural Networks and Deep Learning》中文翻译
2,http://www.cnblogs.com/pinard/p/6494810.html
3,http://blog.csdn.net/yunpiao123456/article/details/52437794

























 1920
1920

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








