《深度学习》——神经网络中的损失函数及正则化惩罚和梯度下降

神经网络中的损失函数及正则化惩罚和梯度下降

• 在神经网络中，损失函数、正则化惩罚和梯度下降是三个关键的概念，它们共同作用于网络的训练过程，以提升网络的性能和泛化能力。
• 神经网络模型结构如下图所示：
  
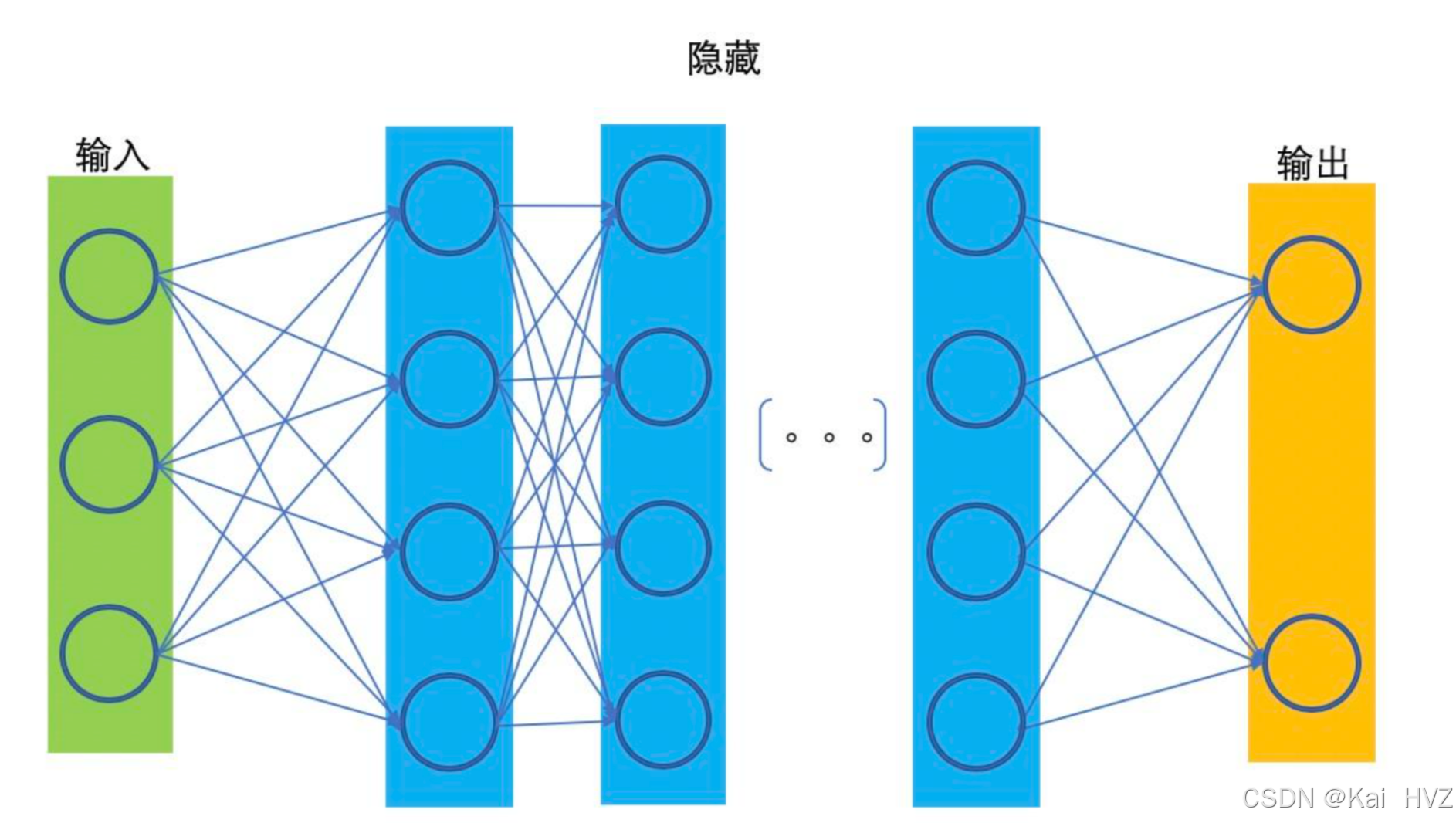
• 在构建好一个神经网络模型后，为了让模型得出的结果更加的准确，那么必须对模进行训练，找到最接近真实结果的模型
• 定义损失函数用来判断模型预测的结果和真实值的误差，在对损失函数添加正则化惩罚项，提高对输入数据的拟合效果，达到好的泛化能力
• 为了达到最小的误差值，需要运用梯度下降的方法来找到模型中最优的权重参数

损失函数

损失函数（Loss Function）用于衡量模型预测结果与真实标签之间的差异程度，它是评估模型性能的重要指标，也是模型训练过程中的优化目标。常见的损失函数有：

• 示例：多分类的情况下，如何计算损失值呢？
  • softmax交叉熵损失函数多用于实现分类问题，用于多分类公式如下：
    
    • yi表示第 i 个预测的结果值
• 下面是猫、狗、羊的照片，标签分别为0、1、2
  
• 如果我们传入猫的照片进行训练，训练过程如下图所示
  
• 首先先对训练后的各目标结果进行e的指数倍放大
• 再将其值进行归一化，得到各个结果的概率
• 最后通过损失函数计算出每个标签结果上的损失值
• 由于我们输入的是猫的照片进行训练，所以只需要关注第一个输出神经元的结果，如果损失值越小，说明越靠近真实结果，模型的效果也就越好

正则化惩罚

正则化惩罚是一种用于防止神经网络过拟合的技术，通过在损失函数中添加额外的惩罚项，来限制模型的复杂度，使模型能够更好地泛化到新的数据。常见的正则化方法有：

• 下面通过一个实例来说明为什么要增加正则化惩罚：
  
• w1和w2与输入的乘积都为1，但w2 与每一个输入数据进行计算后都有数据，使得w2会学习到每一个特征信息。
• 而w1只和第1个输入信息有关系，容易出现过拟合现象，因此w2的效果会比w1 好
• 因此需要引入正则化惩罚项来避免第一种权重值的情况

梯度下降

梯度下降是一种常用的优化算法，用于最小化损失函数，找到使损失函数达到最小值的模型参数。

损失函数用于衡量模型的好坏，正则化惩罚用于防止过拟合，梯度下降用于优化模型参数，它们在神经网络的训练中起着至关重要的作用，相互配合，使得神经网络能够学习到数据中的规律，提高模型的性能和泛化能力。

• 用下图来解释梯度下降的过程：
  • 参数取不同的初始值，可能会得到不同的最小损失值，但是每个初始的参数只是得到了此模型局部的最小损失值
  • 就好像当你处在一个谷底时，只会认为此时的位置是最低的，但并不知道其他的低谷处还有更低的位置
  • 梯度下降就是通过不断地寻找梯度方向和计算得到不同的损失值，直到找到最优和满足条件的值为止