先来来看看随机连续分布下贝叶斯分类器模型。假设当前要使用贝叶斯分类器进行二分类的判别,数据集有随机分布,图像如下:
现在定义代价函数J,其中p1和p2表示已知的二分类出现的先验概率,c11,c12,c21,c22表示对应的经验代价权重参数,这些参数看做常量,X是多元变量的向量形式,C是正态分布下多元变量之间的协方差矩阵,如果多元变量之间是独立的,那么协方差矩阵非对角线元素都是0。公式(Van Trees)有:
然后代入多元高斯分布下的条件概率密度函数,m是数据维度(特征数量)。此处只针对二分类,其中i=1,2:
这样高斯分布下的贝叶斯分类器就退化成了感知器,只需要判断y=wx+b是否大于0即可进行分类。








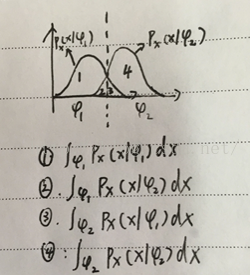


















 4021
4021

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








