线性代数学习笔记4

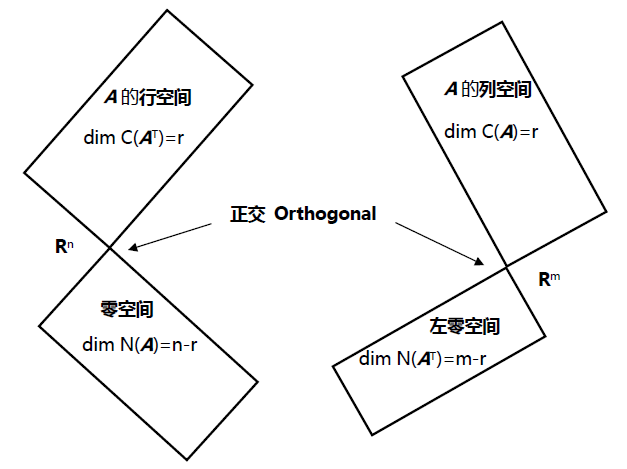
第十四集　　正交向量与正交子空间

正交向量

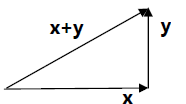
正交就是垂直的另一种说法。两向量正交则$x^{T}y=y^{T}x=0$。当两个向量的夹角为90 度时，按照勾股定理x，y 满足：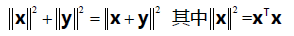
零向量与所有向量都正交。
正交子空间
子空间S 与子空间T 正交，则S 中的任意一个向量都和T 中的任意向量正交。
黑板所在的平面和地板所在平面不是正交关系。比如平面的子空间包括只包含零向量的0 空间、过原点的直线以及整个平面。0 空间和过原点的直线正交；经过原点的两条直线若夹角为直角则互相正交。
零空间与行空间正交
矩阵A 的行空间和它的零空间正交。若x 在零空间内，则有Ax=0，将A 表示为行向量的格式：

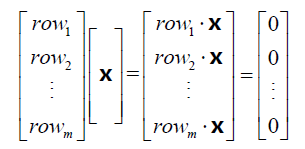
x 与矩阵A 的行向量点积都等于0，则它和矩阵A 行向量的线性组合进行点积也为0，所以x 与A 的行空间正交。x 为零空间内的任意向量，所以零空间与行空间正交。同理可以证明列空间与左零空间正交。
行空间和零空间实际上把$R^{n}$空间分割成了两个正交的子空间。例如对于矩阵：
其行空间是1 维的，向量$[1,2,5]$是它的基向量，而其零空间是垂直于$[1,2,5]$并穿过原点的2 维平面。行空间和零空间不仅仅是正交，并且其维数之和等于n，我们称行空间和零空间为$R^{n}$空间内的正交补。这表示零空间包含所有和行空间正交的向量。
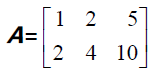
一个空间中正交子空间的维数之和不可能超过原空间的维数。之前提到的黑板和地板平面不是正交子空间的例子，二者都在3 维空间中，分别为2 维空间，2+2>3，因此不可能正交。
可以称目前讨论的这部分内容是线性代数基本定理的第二部分。第一部分是给出四个子空间和它们的维数，第二部分说明它们是两两互为正交补，第三部分讨论子空间的正交基。这些内容都反映在了本讲座开始的那幅图上。
如何求解一个无解方程组Ax=b 的解。
如果A 是长方形矩阵，m 大于n。当左侧方程数特别多的时候，容易混入“坏”数据，方程变得无解。但是对于数据的可信度我们无从判断，线性代数要做的就是在这种条件下求一个方程的“最优解”。矩阵$A^{T}A$会发挥重要作用，它是一个n*n 方阵，并且是对称阵。

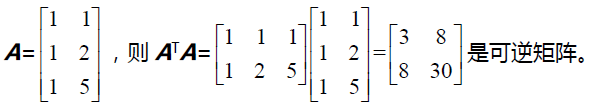
但是矩阵$A^{T}A$并不总是可逆。

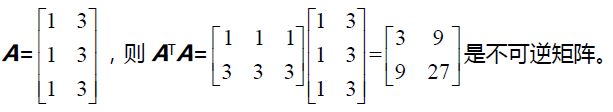
实际上矩阵$A^{T}A$ 的秩等于A 的秩。因此矩阵$A^{T}A$可逆要求A 的列向量线性无关。
本章的核心内容就是当Ax=b 无解的时候，求解$A^{T}A\hat{x}=A^{T}b$得到最优解。

第十五集　　子空间投影
投影（射影）Projections

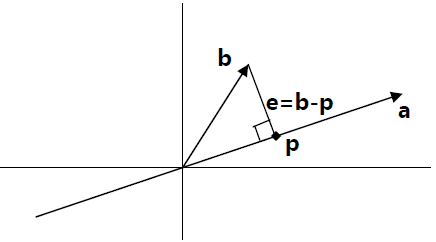
投影问题的几何解释就是：如何在向量a 的方向上寻找与向量b 距离最近的一点。从图中可以看出，这个距离最近的点p，这就是b 在a 上的投影。如果我们将向量p 视为b的一种近似，则长度e=b-p 就是这一近似的误差。因为p 在向量a 的方向上，因此可以令p=xa，而因为它和e 正交，我们可以得到方程：$a^{T}(b-xa)=0$。$x=\frac{ a^{T}b}{ a^{T}a}$，