线性代数学习笔记6

第二十一集　　特征值和特征向量
围绕特征值和特征向量的议题下讨论得都是方阵。
将矩阵A 与向量x 相乘当做是对向量的一种操作或者函数，输入x 而输出Ax。
特征向量即在特定的向量x 方向上输出的Ax 平行于x，即为：
$Ax=\lambda x$
其中x为矩阵A 的特征向量，而$\lambda$为A 的特征值。
例1：矩阵P是朝向某平面的投影矩阵。P将向量b 投影到它距离平面最近的一点p=Pb。

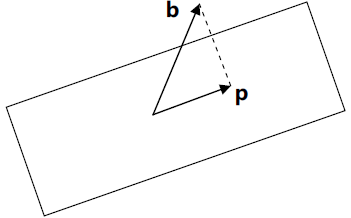
b和Pb不是一个方向的，所以b不是特征向量。
对于这个平面之内的x，均有P x=x，因此x 是特征向量而1 为特征值。垂直于该平面的向量x 经投影得到P x=0，这个x 也是矩阵的特征向量而0 为特征值。矩阵P 的所有特征向量（平面上的特征向量与垂直于该平面的特征向量）张成了整个空间。
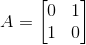
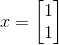
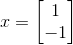
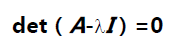
例2：交换矩阵，是用来交换向量$\left ( x_{1} x_{2}\right )$变为$\left ( x_{2} x_{1}\right)$的，即$\left ( x_{1} x_{2}\right )A$=$\left ( x_{2} x_{1}\right)$，$x_{1} x_{2}$为列向量，$A$为列向量线性组合的系数。交换后的$\left ( x_{2} x_{1}\right)$是初始向量$\left ( x_{1} x_{2}\right )$与一个因子的乘积。所以$A$具有特征向量，对应的特征向量为1；另一个特征向量为，对应的特征向量为-1。这些特征向量张成了整个空间。因为是对称矩阵，其特征向量互相垂直。

任意n*n 矩阵A 具有n 个特征值，并且它们的和等于矩阵对角线上的元素之和，这个数值为矩阵的迹。
做如下数学处理：$Ax=\lambda x$，因此有$（A-\lambda I）x=0$。对于不为零向量的x，