最短路径算法之Floyd

Floyd算法是一个求解加权连通图中任意两点之间最短路径的算法，是个很值得品味的算法。 

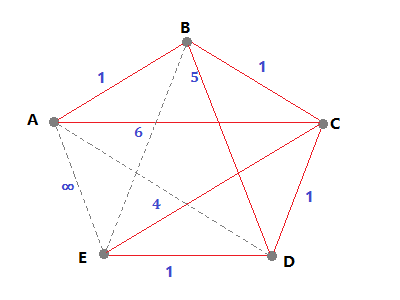
如上图所示，这是一个无向加权连通图，不相连的点用虚线连接，其权值为∞。

我们希望得到A->E的最小距离，根据目测能得到正确结果4（ABCDE走一圈）。

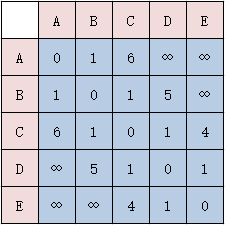
我们把连通图转为邻接矩阵，因为是无向图，所以该图沿对角线对称（如果是有向图则非对称）

Floyd算法所做的就是不断优化该邻接矩阵的路径权值，直到整个任意两点的距离都变为最小距离。

下面上代码，简单到不像寻路算法：

public const int Z = 10000000;
const int VERTEX_COUNT = 5;
public int[,] map = new int[VERTEX_COUNT, VERTEX_COUNT]
					{   {0, 1, 4, 4, 1},
						{1, 0, 1, Z, 3},
						{4, 1, 0, Z, 8},
						{4, Z, Z, 0, Z},
						{1, 3, 8, Z, 0}};
public int[,] path = new int[VERTEX_COUNT, VERTEX_COUNT];

// 核心处理方法
public void DoFloyd()
{
	for (int i = 0; i < VERTEX_COUNT; i++)
	{
		for (int j = 0; j < VERTEX_COUNT; j++)
		{
			path[i, j] = -1;
		}
	}

	for (int k = 0; k < VERTEX_COUNT; k++)
	{
		for (int i = 0; i < VERTEX_COUNT; i++)
		{
			for (int j = 0; j < VERTEX_COUNT; j++)
			{
				if (map[i, j] > map[i, k] + map[k, j])
				{
					map[i, j] = map[i, k] + map[k, j];
					path[i, j] = k;
				}
			}
		}
	}
}

// 获取两点间的距离
public int GetDistance(int from, int to)
{
	return map[from, to];
}

// 获取两点间的路径
public List<int> GetPath(int from, int to)
{
	if (map[from, to] >= Z)
	{
		// 无法连通
		return null;
	}
	List<int> p = new List<int>();
	p.Add(from);
	Stack<int> stack = new Stack<int>();
	stack.Push(to);
	stack.Push(from);
	while (stack.Count > 0)
	{
		from = stack.Pop();
		to = stack.Pop();
		int pass = path[from, to];
		if (pass == -1)
		{
			// 这条边没有被其他点优化，直接走就对了
			p.Add(to);
		}
		else
		{
			// 这条边被优化了，我们拆成两段重新检查。这里用栈模拟递归
			stack.Push(to);
			stack.Push(pass);
			stack.Push(pass);
			stack.Push(from);
		}
	}
	return p;
}

执行Floyd()后，map[0,4]的值就是A->E的最小距离。如果值大于等于z，则表示这两点无法连通。GetPath(0,4)方法会返回内容为0, 1, 2, 3, 4的数组，表明从A点出发，途经B、C、D最后到E点。

下面说说该算法的原理：
假设A->C的直线距离用map[A,C]表示，那么经过第三点B的A->B->C的距离等于map[A,B]+map[B,C]。
如果 map[A,B]+map[B,C] < map[A,C]，那么我们更新map[A,B] = map[A,B]+map[B,C]，也就表示此时A->C的直线距离被更新了。同时在path表里也填上path[A,B]=C，表示C点优化了连线AB。
代码中有三重循环，里面的两重循环是用来遍历所有直线路径map[i, j]的，最外面的循环是用来遍历第三点k的，最后使得每条路径都被每个第三点优化过。
接下来我们看A->E的路径优化中先后发生了哪些事情：

1. map[A,C]被中间点B优化了，map[A,C]=map[A,B]+map[B,C]=2，path[A,C]=B
2. map[A,D]被中间点C优化了，map[A,D]=map[A,C]+map[C,D]=3，path[A,D]=C
3. map[A,E]被中间点D优化了，map[A,E]=map[A,D]+map[D,E]=4，path[A,E]=D

最后的结果是：GetDistance(A, E) = 4，GetPath(A, E) = (A,B,C,D,E)。

再看下GetPath的工作流程：

1. 输出起始点A，将(A,E)入栈待查
2. (A,E)出栈，发现path[A,E]=D，将(D,E)和(A,D)入栈待查
3. (A,D)出栈，发现path[A,D]=C，将(C,D)和(A,C)入栈待查
4. (A,C)出栈，发现path[A,C]=B，将(B,C)和(A,B)入栈待查
5. (A,B)出栈，发现path[A,B]=-1，表明A->B无需绕路，输出B
6. (B,C)出栈，发现path[B,C]=-1，表明B->C无需绕路，输出C
7. (C,D)出栈，发现path[C,D]=-1，表明C->D无需绕路，输出D
8. (D,E)出栈，发现path[D,E]=-1，表明D->E无需绕路，输出E
9. 栈空，寻路结束

你可能会发现，这不是递归操作么，其实这里就是用栈模拟的递归。

在优化路径的过程中，优化会在每条路径上不断叠加，最后使得整个邻接矩阵的任意两点间都是最小距离。

而且每当一个点X优化了某条线路P->Q，就记录path[P->Q]=X，每条边都很可能会先后被多个点优化，我们记录最后一个优化它的点就好。

Floyd算法的时间复杂度为O(n^3)，三重循环。空间复杂度为O(n^2)，二维数组。因为计算量只跟顶点数目有关，所以在稠密连通图中效率要比Dijkstra之流要好很多。

最后给出三个小思考思考，解决了它们才能证明你搞懂了Floyd算法，试试吧：

1. 三重循环中，第三点k的遍历放在最里层会导致什么问题？

2. k的遍历如果是逆向的甚至是乱序的，能不能得到正常结果？

3. 三重循环内的 path[i, j] = k 这一句如果改成 path[i, j] = path[i, j] == -1 ? k : path[i, j] ，即只能赋值一次，GetPath()得到的路径正确吗？