S型隶属函数（Sigmoid Membership Function）的详细介绍及python示例

        S型隶属函数是一种基于Sigmoid函数的模糊隶属函数，其形状呈现平滑的“S”形曲线，适合描述单调递增或递减的模糊集合。它在模糊逻辑中常用于表示变量逐渐过渡到某一状态的过程，例如“温度逐渐升高”或“湿度逐渐降低”。

那么为什么对这样一个隶属函数有现实需求呢？

一、回顾隶属函数的作用

        前文，我们已经解读过了三角形隶属函数、梯形隶属函数和高斯隶属函数，其中三角形和梯形在一个区间内都是线性变化的，高斯虽然不是线性变化，但依然是单峰和对称的。这些隶属函数在一定程度解决了输入变量到模糊集合的隶属程度问题。

        具体内容可以看我的CSDN文章：模糊逻辑和模糊集合理论的核心概念（隶属函数）及示例-CSDN博客

        如前文使用三角形隶属函数对温度T进行处理的例子：

        其中，a表示左边界（隶属度为0的点），b表示顶点（隶属度为1的点），c表示右边界（隶属度为0的点）。

        其中，a表示左边界（隶属度为0的点），b表示左顶点（隶属度从0上升到1的点），c表示右顶点（隶属度从1下降到0的点），d表示右边界（隶属度为0的点）。

        经过隶属函数处理，确定输入变量的真实值所隶属的模糊集合，得到模糊化的输出结果，为后续与生成的模糊规则库进行匹配做准备。

        经以上分析，可知，三角形隶属函数、梯形隶属函数和高斯隶属函数依然很难较真实的描述现实世界的需求：如人对温度/湿度的感知并非线性的。

        示例文章：“系统建模：基于模糊逻辑的冷气阀门控制系统（T-S推理Python示例）”，网址：https://lzm07.blog.csdn.net/article/details/146405477

二、S型隶属函数数学定义

        S型函数通常是指类似于逻辑函数的S形曲线，比如sigmoid函数，它在0到1之间变化，中间有一个平滑的过渡。S型隶属函数就是基于这种形状的函数，用来表示某个变量属于某个模糊集合的程度，尤其是在需要表示单调递增或递减的情况。

        S型隶属函数基于Sigmoid函数，具有独特的“S”形曲线，适合描述变量从非隶属到完全隶属（或相反）的平滑过渡过程。

        标准的sigmoid函数是：

        S型隶属函数的核心是Sigmoid函数，通过参数控制曲线的陡峭程度和中心点：

        （1）递增S型（左肩型，左右边界的参数，例如起始点a和终止点b，当x在a和b之间时，隶属度可能从0开始逐渐增加到1，可用于描述“逐渐升高”的隶属关系），μ(x)是一个分段函数，分为四个区间，每个区间对应一个表达式：

        更常见的可能是使用sigmoid函数的变体，比如：

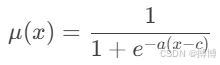
         （2）递减S型（右肩型，从1逐渐减少到0，可用于描述“逐渐降低”的隶属关系）：

        其中：a表示斜率参数，控制曲线的陡峭程度（|a|越大，曲线越陡峭）。c表示中心点，隶属度为0.5的位置（即x=c 时μ(x)=0.5）。在中间点c处增长最快，适用于表示变量逐渐过渡到某个状态的情况。

        这种情况下，当x趋近于负无穷，μ(x)趋近于0；当x趋近于正无穷，μ(x)趋近于1。这种函数适合表示“高”或者“低”这种单边的情况，比如温度逐渐升高到某个点时，隶属度从低变高。

三、特点

（一）优点

1.平滑性与连续性

S型函数是连续且可导的，能够描述自然渐变过程，避免了隶属度的突变。

适合需要平滑输出的场景（如高精度控制、自然语言描述）。

2.参数灵活

通过调整参数a（斜率）和c（中心点），可以控制曲线的陡峭程度和过渡位置：

（1）a 越大，曲线越陡峭，隶属度变化越快（如a=2）。

（2）c 控制中心点，即隶属度为0.5的位置（如c=5 时，x=5 时μ(x)=0.5）。

3.单边隶属能力

递增S型：适合描述“逐渐升高”的隶属关系（如“高温”）。

递减S型：适合描述“逐渐降低”的隶属关系（如“低温”）。

4.数学简洁性

公式简单，易于实现和计算，适合嵌入实时系统。

（二）缺点

1.单边性限制：只能描述单方向变化的模糊集合（如“高”或“低”），无法直接描述对称或双峰集合（如“中等温度”需结合其他函数）。

2.参数敏感性：参数a 和c 的调整需要经验，陡峭度过高（如a=10）可能导致隶属度突变，失去模糊性。

3.计算复杂度：相比三角形或梯形隶属函数，Sigmoid函数涉及指数运算，计算成本略高（但对现代硬件影响较小）。

4.不适用于对称场景：无法像高斯函数或三角形函数那样自然描述对称的模糊概念（如“接近目标值”）。

（三）与其他隶属函数的对比

隶属函数	优点	缺点	适用场景
S型	平滑过渡，参数灵活，单边描述能力强	无法描述对称集合，参数调整敏感	单方向渐变过程（如风险升高）
三角形/梯形	计算高效，直观易解释	隶属度突变，不适合平滑过渡	简单分类（如“低/中/高”）
高斯型	对称且平滑，适合自然现象	计算复杂，参数意义不直观	对称模糊集合（如“接近目标值”）
Z型/Π型	可组合实现复杂形状	参数多，设计复杂	特殊需求（如非对称多峰集合）

四、应用场景

1.模糊控制系统

（1）温度控制：描述“温度逐渐升高”或“温度逐渐降低”的隶属度（如空调系统）。

（2）自动驾驶：定义“接近障碍物”的隶属度，距离越近隶属度越高。

2.分类与阈值判定

医疗诊断：如“血糖偏高”的隶属度随血糖值递增。

图像处理：像素亮度“接近白色”的隶属度判定。

3.风险评估与决策系统

金融风控：风险等级从“低”到“高”的平滑过渡。

工业控制：设备磨损程度的隶属度评估（如“磨损严重”）。

4.自然语言处理（NLP）

描述模糊概念，如“非常满意”或“略微不满”的情感强度。

如何选择S型隶属函数

（1）何时选择S型隶属函数：需要描述单方向渐变过程（如“风险逐渐升高”）、要求平滑输出，且对计算资源不敏感的场景。

（2）何时避免使用：需要对称描述（如“中等温度”）或追求极致计算效率时，优先选择三角形、梯形或高斯函数。

五、Python实现与可视化

1.S型隶属函数python实现

        以下是使用Python生成和绘制S型隶属函数的代码示例：

import numpy as np

import matplotlib.pyplot as plt



def sigmoid_mf(x, a, c, is_increasing=True):

    """

    计算S型隶属函数的值

    :param x: 输入值

    :param a: 斜率参数（控制陡峭程度）

    :param c: 中心点（隶属度为0.5的位置）

    :param is_increasing: True表示递增S型，False表示递减S型

    :return: 隶属度

    """

    sigmoid = 1 / (1 + np.exp(-a * (x - c)))

    return sigmoid if is_increasing else 1 - sigmoid



# 定义参数

a_increasing = 1.0  # 递增S型的斜率

c_increasing = 5.0   # 中心点

a_decreasing = -1.0  # 递减S型的斜率（负号表示方向）

c_decreasing = 5.0   # 中心点



# 生成输入值

x_values = np.linspace(0, 10, 1000)



# 计算隶属度

y_increasing = [sigmoid_mf(x, a_increasing, c_increasing) for x in x_values]

y_decreasing = [sigmoid_mf(x, a_decreasing, c_decreasing, is_increasing=False) for x in x_values]



# 绘制图形

plt.figure(figsize=(8, 4))

plt.plot(x_values, y_increasing, label=f'Increasing S-Curve: a={a_increasing}, c={c_increasing}')

plt.plot(x_values, y_decreasing, '--', label=f'Decreasing S-Curve: a={a_decreasing}, c={c_decreasing}')

plt.title('Sigmoid Membership Functions')

plt.xlabel('x')

plt.ylabel('Membership Degree')

plt.legend()

plt.grid(True)

plt.show()

2.代码说明：

（1）sigmoid_mf函数：根据输入值x 和参数a,c 计算隶属度。is_increasing 控制递增或递减。

（2）参数设置：

递增S型：a=1.0,c=5.0，曲线在x=5 处隶属度为0.5，向右逐渐升高。

递减S型：a=-1.0,c=5.0，曲线在x=5 处隶属度为0.5，向右逐渐降低。

（3）绘图：使用Matplotlib绘制递增和递减的S型曲线，虚线表示递减。

3.运行结果

运行代码后，将生成包含两条曲线的图形（重叠了）：

（1）递增S型：从左侧的0平滑过渡到右侧的1，中心点在x=5。

（2）递减S型：从左侧的1平滑过渡到右侧的0，中心点同样在x=5。

4.参数调整

（1）调整斜率 a：

a=2.0：曲线更陡峭，过渡更快（如下图的实线）。

a=0.5：曲线更平缓，过渡更慢（如下图的虚线）。

（2）调整中心点c：

c=3.0：曲线中心左移，隶属度0.5的位置提前（如下图的实线）。

c=7.0：曲线中心右移，隶属度0.5的位置延后（如下图的虚线）。

六、组合应用示例

        在模糊系统中，可以结合递增和递减S型函数描述复杂逻辑。例如：

# 定义两个S型函数（一个递增，一个递减）

y_combined = np.minimum(

    sigmoid_mf(x_values, a=1.0, c=3.0, is_increasing=True),

    sigmoid_mf(x_values, a=-1.0, c=7.0, is_increasing=False)

)



# 绘制组合曲线

plt.figure(figsize=(8, 4))

plt.plot(x_values, y_combined, label='Combined S-Curves (Intersection)')

plt.title('Combined Sigmoid Membership Functions')

plt.xlabel('x')

plt.ylabel('Membership Degree')

plt.legend()

plt.grid(True)

plt.show()

        此代码生成两个S型曲线的交集，描述类似“中等范围”的模糊集合。完整代码如下：

import numpy as np

import matplotlib.pyplot as plt



def sigmoid_mf(x, a, c, is_increasing=True):

    """

    计算S型隶属函数的值

    :param x: 输入值

    :param a: 斜率参数（控制陡峭程度）

    :param c: 中心点（隶属度为0.5的位置）

    :param is_increasing: True表示递增S型，False表示递减S型

    :return: 隶属度

    """

    sigmoid = 1 / (1 + np.exp(-a * (x - c)))

    return sigmoid if is_increasing else 1 - sigmoid



# 生成输入值

x_values = np.linspace(0, 10, 1000)



# 定义两个S型函数（一个递增，一个递减）

y_combined = np.minimum(

    sigmoid_mf(x_values, a=1.0, c=3.0, is_increasing=True),

    sigmoid_mf(x_values, a=-1.0, c=7.0, is_increasing=False)

)



# 绘制组合曲线

plt.figure(figsize=(8, 4))

plt.plot(x_values, y_combined, label='Combined S-Curves (Intersection)')

plt.title('Combined Sigmoid Membership Functions')

plt.xlabel('x')

plt.ylabel('Membership Degree')

plt.legend()

plt.grid(True)

plt.show()

        组合后的效果如下图所示：

        通过调整参数和组合函数，S型隶属函数能够灵活适应不同的模糊逻辑需求，为系统提供平滑且自然的过渡特性。