matlab多次拟合曲线效果比较

本博文源于matlab多项式章节的一个小知识，很多同学觉得拟合polyfit会用就行了，知道最小二乘法是拟合的原理。其中包含多元函数积分学的知识。但是大家是否真的有空把多次拟合的函数跑一遍总结规律呢？还有过拟合和欠拟合是否能在论文中使用呢？所谓过拟合就是能近似经过每一点，但是曲线过于弯曲形态不好。而欠拟合就是连点都不怎么过，看上去就是很丑陋，很low的模样。

下面通过一个例子去看一下，拟合的次数看出拟合多次是否能对函数有更好的逼近，并能说出哪种次数是过拟合？

例子：现有一组实验数据：x的取值是从1到2之间的数，间隔为0.1,y的值为下列数据，要求分别用二次、三次和七次来拟合数据，观察效果

y的值

2.1
3.2
2.1 
2.5 
3.2
3.5
3.4
4.1
4.7
5.0
4.8

代码程序

>> x=1:0.1:2;
>> y=[2.1 3.2 2.1 2.5 3.2 3.5 3.4 4.1 4.7 5.0 4.8];
>> p2=polyfit(x,y,2)

p2 =

    1.3869   -1.2608    2.1410

>> p3=polyfit(x,y,3)

p3 =

   -5.1671   24.6387  -35.2187   18.2002

>> p7=polyfit(x,y,7)

p7 =

  1.0e+005 *

    0.0287   -0.3069    1.3966   -3.4977    5.2059   -4.6033    2.2386   -0.4617

>> x1=x;
>> y2=polyval(p2,x1);
>> y3=polyval(p3,x1);
>> y7=polyval(p7,x1);

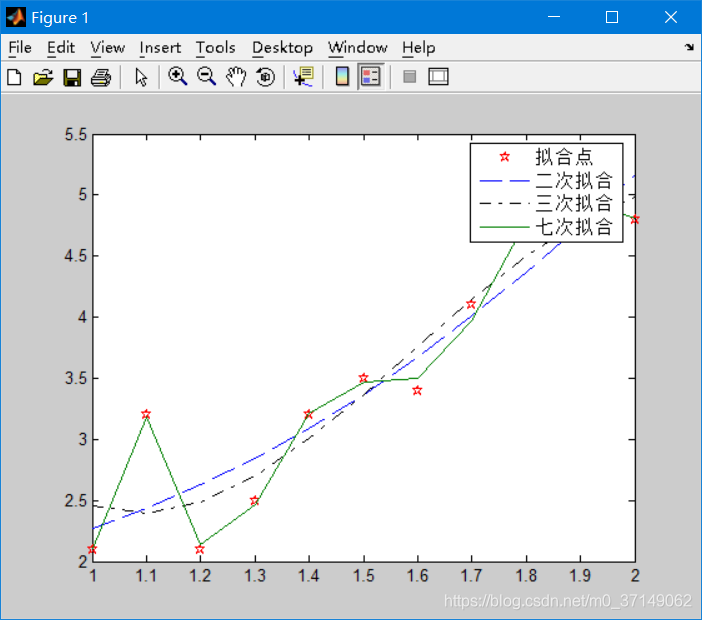
>> plot(x,y,'rp',x1,y2,'--',x1,y3,'k-.',x1,y7)
>> legend('拟合点','二次拟合','三次拟合','七次拟合')
>> 

清晰易懂附上图，其中polyfit就是拟合常用函数,polyval就是一个求值函数方便plot画图

总结

图上看出拟合次数越高越好，但是拟合太高可能浮动越大，因此一般不会超出七次。大家在使用中二次拟合起步。